35 câu hỏi
Trong các câu dưới đây, câu nào là mệnh đề?
Có ai ở trong đó không?;
Bạn có thấy đói không?;
Đừng lại gần tôi!;
Số 25 không phải là số nguyên tố.
Cho tập hợp A = {2; 4; 6; 8}. Số tập con của tập hợp A là?
15;
16;
17;
18.
Cho tập hợp K = [1 ; 7) \ (– 3 ; 5). Khẳng định nào sau đây đúng ?
K = [1; 7);
K = (– 3; 7);
K = [1; 5);
K = [5; 7).
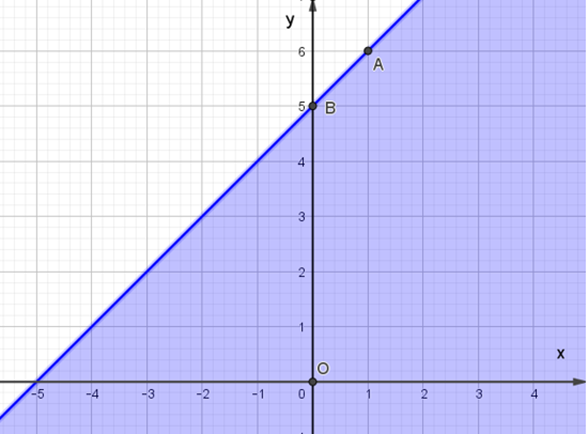
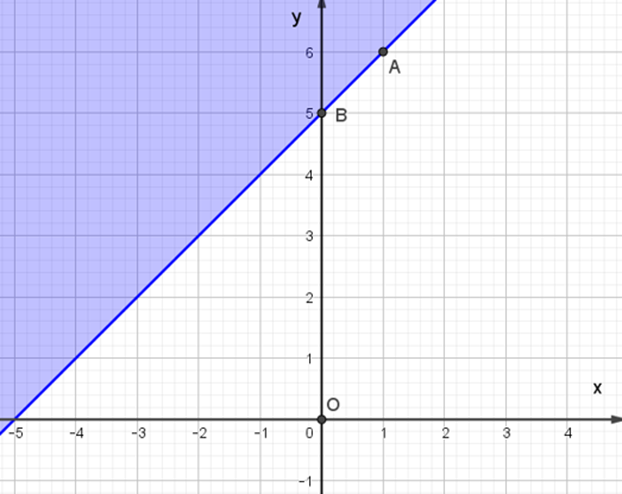
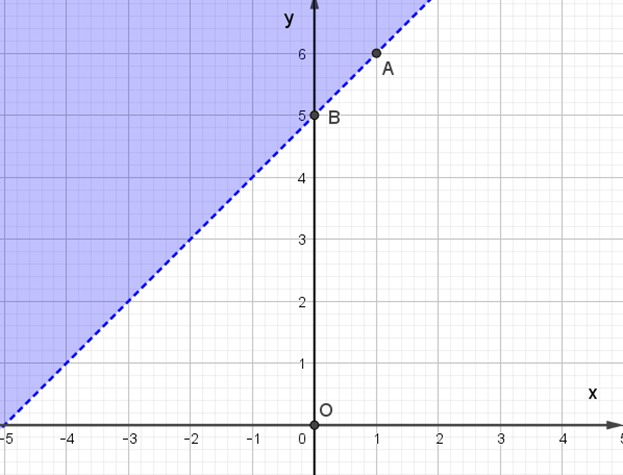
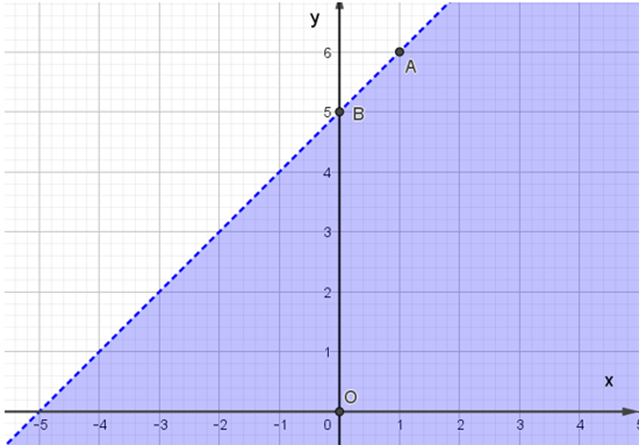
Miền nghiệm của bất phương trình x – y + 5 ≥ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
Cặp số nào sau đây là nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}2x - 1 > 0\\x + 5y < 4\end{array} \right.\) ?
(3; 5);
(1; –1);
(2; 5);
(3; 4).
Chọn phương án SAI trong các phương án dưới đây?
sin 0° = 0;
cos 90° = 0;
cos 0° = 1;
sin 90° = 0.
Cho β là góc tù. Tìm khẳng định đúng trong các khẳng định dưới đây?
cos β > 0;
sin β > 0;
tan β > 0;
cot β > 0.
Cho góc α thỏa mãn \(\sin \alpha = \frac{{12}}{{13}}\) và 90° < α < 180°. Tính cosα.
\(\cos \alpha = \frac{2}{{13}}\);
\(\cos \alpha = \frac{5}{{13}}\);
\(\cos \alpha = - \frac{5}{{13}}\);
\(\cos \alpha = - \frac{2}{{13}}\).
Cho tam giác ABC biết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) và \(AB = 2\sqrt 2 \). Tính AC.
\(2\sqrt 2 \);
\(2\sqrt 3 \);
\(2\sqrt 6 \);
2\(\sqrt 5 \).
Cho hình bình hành ABCD có K là giao điểm hai đường chéo như hình vẽ.
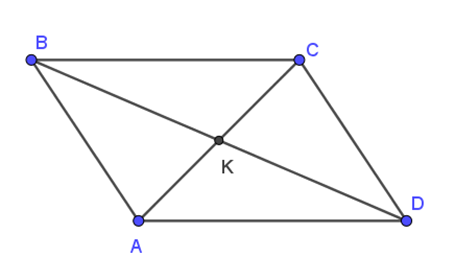
Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AK} \) và \(\overrightarrow {KC} \) cùng phương ngược hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng phương cùng hướng;
\(\overrightarrow {KC} \) và \(\overrightarrow {KA} \) cùng phương ngược hướng;
\(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) cùng phương cùng hướng.
Cho hình bình hành ABCD có AB = 4 cm. Tính độ dài vectơ \(\overrightarrow {CD} \).
1 cm;
3 cm;
4 cm;
2 cm
Cho các điểm A, B, C phân biệt. Đẳng thức nào sau đây đúng ?
\(\overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {CA} \);
\(\overrightarrow {AB} = \overrightarrow {CB} + \overrightarrow {AC} \);
\(\overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {AC} \);
\(\overrightarrow {AB} = \overrightarrow {CA} + \overrightarrow {BC} \).
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
\(\overrightarrow {AB} - \overrightarrow {AI} = \overrightarrow {BI} \);
\(\overrightarrow {AB} - \overrightarrow {DA} = \overrightarrow {BD} \);
\(\overrightarrow {AB} - \overrightarrow {DC} = \overrightarrow 0 \);
\(\overrightarrow {AB} - \overrightarrow {DB} = \overrightarrow 0 \).
Cho hình vuông ABCD cạnh 2a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {DA} } \right|\).
\(a\sqrt 2 \);
a;
\(2a\sqrt 2 \);
2a.
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \);
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AB} \);
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AC} \);
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {BC} \).
Cho tam giác ABC. Đặt \(\overrightarrow {AB} = \overrightarrow a \), \(\overrightarrow {AC} = \overrightarrow b \). M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích \(\overrightarrow {AN} \) qua các vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ta được biểu thức là:
\[2\overrightarrow a + 3\overrightarrow b \];
\[ - 2\overrightarrow a + 3\overrightarrow b \];
\[2\overrightarrow a - 3\overrightarrow b \];
\[2\overrightarrow a + \overrightarrow b \].
Cho các vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương và \(\overrightarrow x = \overrightarrow a - 3\overrightarrow b \), \(\overrightarrow y = 2\overrightarrow a + 6\overrightarrow b \) và \(\overrightarrow z = - 3\overrightarrow a + \overrightarrow b \). Khẳng định nào sau đây là đúng ?
\(\overrightarrow y \), \(\overrightarrow z \) cùng phương, ngược hướng;
\(\overrightarrow y \), \(\overrightarrow z \) cùng phương, cùng hướng;
\(\overrightarrow y \), \(\overrightarrow x \) cùng phương, ngược hướng;
\(\overrightarrow y \), \(\overrightarrow x \) cùng phương, cùng hướng.
Cho tam giác ABC có điểm I nằm trên cạnh AC sao cho \(\overrightarrow {BI} = \frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \), J là điểm thỏa mãn \(\overrightarrow {BJ} = \frac{1}{2}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} \). Ba điểm nào sau đây thẳng hàng ?
I, J, C;
I, J, B;
I, A, B;
I, G, B.
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính \(\left( {\overrightarrow {CB} ,\overrightarrow {CA} } \right)\).
90°;
60°;
30°;
45°.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Biết: \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 30^\circ \), \(\overrightarrow a .\overrightarrow b = \sqrt 3 \)và \(\left| {\overrightarrow b } \right| = 2\). Tính độ dài của vectơ \(\overrightarrow a \).
1;
2;
\(\frac{1}{2}\);
\(\frac{1}{4}\).
Cho tam giác ABC đều cạnh a. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
a;
0;
a2;
\(\frac{1}{2}{a^2}\).
Cho hình thang ABCD với hai đáy là AB, CD có: \(\left( {\overrightarrow {AB} - \overrightarrow {AD} } \right).\overrightarrow {AC} = 0\). Khẳng định nào sau đây là đúng ?
BD vuông góc với AC;
AB vuông góc với AC;
AB vuông góc với DC;
BD vuông góc với DC.
Cho giá trị gần đúng của \(\frac{6}{{17}}\) là 0,35. Sai số tuyệt đối của số gần đúng 0,35 là:
0,003;
0,03;
0,0029;
0,02.
Hãy viết số quy tròn của số gần đúng a = 15,318 biết \(\overline a \) = 15,318 ± 0,05.
15,3;
15,31;
15,32;
15,4.
Số lượng khách từ ngày thứ nhất đến ngày thứ 10 của một nhà hàng mới mở được thống kê ở bảng sau:
|
Ngày |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số khách |
11 |
9 |
7 |
5 |
15 |
20 |
9 |
6 |
17 |
13 |
Tính số khách trung bình từ bảng số liệu trên.
9,2;
10,2;
11,2;
12,2.
Tìm trung vị của mẫu số liệu sau:
1; 0; 5; 10; 2; 3; 9.
3;
5;
0;
2.
Cho mẫu số liệu sau:
1; 9; 12; 10; 2; 9; 15; 11; 20; 17.
Tứ phân vị Q1, Q2, Q3 của mẫu số liệu trên lần lượt là:
9; 11; 15;
2; 10,5; 15;
10; 12,5; 15;
9; 10,5; 15.
Cho mẫu số liệu sau:
2; 5; 9; 12; 15; 5; 20.
Tìm mốt của mẫu số liệu trên.
5;
9;
12;
20.
Cho mẫu số liệu sau:
15; 26; 5; 2; 9; 5; 28; 30; 2; 26.
Tính khoảng biến thiên của mẫu số liệu trên.
26;
28;
30;
32.
Cho mẫu số liệu sau:
2; 9; 12; 16; 3; 5; 12; 33; 24; 27.
Tính khoảng tứ phân vị của mẫu số liệu trên.
17;
18;
19;
20.
Cho mẫu số liệu sau:
12; 2; 6; 13; 9; 21.
Tìm phương sai của mẫu số liệu trên (làm tròn đến hàng phần trăm).
35,85;
34,85;
34,58;
35,58.
Cho mẫu số liệu sau:
24; 16; 12; 5; 9; 3.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
7,04;
8,04;
7,55;
8,55.
Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 2) và B(3; – 1). Độ dài vectơ \(\overrightarrow {AB} \) là:
5;
3;
\(\sqrt {13} \);
\(\sqrt {15} \).
Trong mặt phẳng tọa độ, cho \(\overrightarrow u = 3\overrightarrow i - 5\overrightarrow j \). Khi đó tọa độ của vectơ \(\overrightarrow u \) là
\(\overrightarrow u = \left( {3;\,\,5} \right)\);
\(\overrightarrow u = \left( {3;\,\, - 5} \right)\);
\(\overrightarrow u = \left( { - 3;\,\,5} \right)\);
\(\overrightarrow u = \left( { - 3;\,\, - 5} \right)\).
Góc giữa vectơ \(\overrightarrow a = \left( {1; - 1} \right)\) và vectơ \(\overrightarrow b = \left( { - 2;0} \right)\) có số đo bằng:
90°;
0°;
135°;
45°.
Gợi ý cho bạn
Xem tất cảĐề thi Học kì 1 Toán 10 - Bộ sách Kết nối tri thức - Đề 01
Đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 2