(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 4)
34 câu hỏi
Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R})\) ở hình bên có đường tiệm cận xiên là một trong bốn đường thẳng dưới đây, đường thẳng đó là đường nào?
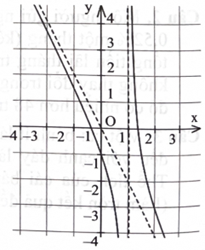
\({\rm{y}} = 2{\rm{x}}.\)
\({\rm{x}} = 1.\)
\({\rm{y}} = - 2{\rm{x}}.\)
\(y = - 3x.\)
Nếu một khối chóp có diện tích mặt đáy bằng S và có chiều cao bằng h thì có thể tích bằng
\(\frac{{{\rm{Sh}}}}{3}.\)
Sh.
3 Sh.
\(\frac{{\pi {\rm{Sh}}}}{3}.\)
Tất cả các nghiệm của phương trình \(\cos x = \frac{{ - \sqrt 2 }}{2}\) là
\(x = \frac{{3\pi }}{4} + {\rm{k}}\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
\({\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}\frac{\pi }{2},{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}\frac{\pi }{2},\forall {\rm{k}} \in \mathbb{Z}.\)
\({\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}2\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}2\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
\({\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}3\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}3\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
Nếu cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công bội \(q = 3\) thì số hạng \({u_n}\) bằng
\({3^{\rm{n}}}.\)
\({3^{{\rm{n}} - 1}}.\)
\({3^{{\rm{n}} + 1}}.\)
\(3 + ({\rm{n}} - 1) \cdot 3.\)
Tập nghiệm của bất phương trình \({\log _{0,5}}x > 4\) là
\(\left( {{4^{0,5}}; + \infty } \right).\)
\(\left( { - \infty ;{4^{0,5}}} \right).\)
\((0;2).\)
\(\left( {0;{{(0,5)}^4}} \right).\)
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow {\rm{u}} = ( - {\rm{a}};{\rm{b}};{\rm{c}}),{\overrightarrow {\rm{u}} ^\prime } = (1; - 2;3).\) Toạ độ của vectơ \(\overrightarrow {\rm{u}} + \overrightarrow {{u^\prime }} \) là
\(( - {\rm{a}} + 1;{\rm{b}} - 2;{\rm{c}} + 3).\)
\(({\rm{a}} + 1;{\rm{b}} - 2;{\rm{c}} + 3).\)
\(( - {\rm{a}} + 1;{\rm{b}} + 2;{\rm{c}} + 3).\)
\((a + 1;b + 2;{\rm{c}} + 3).\)
Trong không gian Oxyz, tọa độ của vectơ \(\overrightarrow {\rm{u}} = 2\overrightarrow {\rm{j}} - 3\overrightarrow {\rm{k}} \) là
\((0; - 2; - 3).\)
\((0; - 2;3).\)
\((0;2; - 3).\)
\((0;2;3).\)
Phát biểu nào sau đây là đúng về mối quan hệ của các đường thẳng trong không gian?
Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b song song với nhau.
Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b vuông góc với nhau.
Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b không có điểm chung
Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) cắt nhau và cùng vuông góc với đường thẳng c thì đường thẳng c vuông góc với mặt phẳng chứa a và b.
Nếu hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục và nhận giá trị dương trên tập số thực thì diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\), trục Ox và các đường thẳng \({\rm{x}} = 7;{\rm{x}} = 9\) bằng
\(\int_9^7 | f(x)|dx.\)
\(\int_7^9 f (x)dx.\)
\(\pi \int_7^9 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.\)
\(\pi \int_9^7 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.\)
Nếu các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,2;{\rm{P}}({\rm{B}}) = 0,5\) thì
\({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,3.\)
\({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,7.\)
\({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,01.\)
\({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,4.\)
Phát biểu nào sau đây là đúng?
\(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \ln (1 - 2{\rm{x}}) + C.\)
\(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \ln |1 - 2{\rm{x}}| + C.\)
\(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \frac{1}{2}\ln |1 - 2{\rm{x}}| + C.\)
\(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \frac{{ - 1}}{2}\ln |1 - 2{\rm{x}}| + C.\)
Cho hình chóp \({\rm{S}}.{\rm{ABCD}}\) có tất cả các cạnh bằng nhau. Số đo góc giữa hai đường thẳng SA và CD bằng
\({60^o }.\)
\({30^o }.\)
\({45^o }.\)
\({90^o }.\)
a) Diện tích của đáy nhỏ là \(16{\rm{d}}{{\rm{m}}^2}.\)
b) Diện tích của đáy lớn là \(24{\rm{d}}{{\rm{m}}^2}.\)
c) Chiều cao của khối bê tông là 4 cm.
d) Thể tích của khối bê tông (làm tròn đến hàng đơn vị của \({\rm{d}}{{\rm{m}}^3}\)) là \(101{\rm{d}}{{\rm{m}}^3}.\)
a) Hai vectơ \(\overrightarrow {\rm{u}} (1;2;3),\overrightarrow {\rm{u}} (3;2;1)\) lần lượt là vectơ chỉ phương của \(\Delta ,{\Delta ^\prime }.\)
b) Điểm \({\rm{M}}( - 1; - 5; - 9)\) không thuộc đường thẳng \(\Delta \), điểm \({{\rm{M}}^\prime }( - 6; - 3;0)\) không thuộc đường thẳng \({\Delta ^\prime }.\)
c) \(\left[ {\overrightarrow {\rm{u}} ,\overrightarrow {{{\rm{u}}^\prime }} } \right] = ( - 4;8; - 4).\)
d) Hai đường thẳng \(\Delta ,{\Delta ^\prime }\) 'chéo nhau.
a) \(I = - \int_a^5 | x - 5|dx + \int_5^b | x - 5|dx\)
b) \(\int_a^5 | x - 5|dx = \int_a^5 {(5 - x)} dx = \left. {\left( {5x - \frac{{{x^2}}}{2}} \right)} \right|_a^5 = \frac{{25}}{2} - \left( {5a - \frac{{{a^2}}}{2}} \right).\)
c) \(\int_5^b | x - 5|dx = \int_5^b {(x - 5)} dx = \left. {\left( {\frac{{{{\rm{x}}^2}}}{2} - 5{\rm{x}}} \right)} \right|_5^{\rm{b}} = \left( {\frac{{{{\rm{b}}^2}}}{2} - 5\;{\rm{b}}} \right) + \frac{{25}}{2}\)
d) \(I = \frac{{{a^2} + {b^2}}}{2} - 5a - 5b + 50\)
a) \({\rm{P}}(\overline {\rm{B}} ) = \frac{3}{5}.\)
b) \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = \frac{1}{3}.\)
c) \({\rm{P}}({\rm{A}}\mid \overline {\rm{B}} ) = \frac{1}{2}.\)
d) \({\rm{P}}({\rm{A}}) = \frac{1}{2}.\)
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về cân nặng của một số quả bưởi da xanh ở một khu vực (đơn vị: kg).
Nhóm | [1,2 ; 1,3) | [1,3 ; 1,4) | [1,4 ; 1,5) | [1,5 ; 1,6) | [1,6 ; 1,7) |
Tần số | 8 | 21 | 8 | 7 | 6 |
Số trung bình của mẫu số liệu ghép nhóm trên là bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \({x^2} + {y^2} + {z^2} - 2x - 4{\rm{y}} + 6{\rm{z}} - 67 = 0.\) Bán kính của mặt cầu bằng bao nhiêu?
Trong không gian với hệ tọa độ Oxyz, góc giữa đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = t}\\{z = - \sqrt 3 t}\end{array}} \right.\) và mặt phẳng \((P):\sqrt 3 y - z - 1 = 0\) là \({n^o }\) với \(n\) là số thực. Giá trị của \(n\) là bao nhiêu?
Một vật chuyển động theo quy luật \(s(t) = 6{t^2} - {t^3}\) với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Trong khoảng 6 giây kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là \({\rm{xm}}/{\rm{s}}.\) Giá trị của x là bao nhiêu?
Nhân ngày khai trương siêu thị MC, các khách hàng vào siêu thị được đánh số thứ tự là các số tự nhiên liên tiếp và có thể được tặng quà (khách hàng đầu tiên được đánh số thứ tự là số 1 ). Cứ 4 khách vào MC thì khách thứ tư được tặng một cái lược chải tóc, cứ 5 khách vào MC thì khách thứ năm được tặng một cái khăn mặt, cứ 6 khách vào MC thì khách thứ sáu được tặng một hộp kem đánh răng. Sau 30 phút mở cửa, có 200 khách đầu tiên vào MC và tất cả khách vẫn ở trong MC. Chọn ngẫu nhiên một khách trong 200 khách đầu tiên, xác suất để chọn được khách hàng được tặng cả ba món quà bằng \(\frac{{\rm{a}}}{{\rm{b}}}\) với \({\rm{a}},{\rm{b}}\) là các số nguyên dương và \({\rm{b}} < 400.\) Giá trị của \({\rm{a}} - {\rm{b}}\) là bao nhiêu?
Hai bạn Việt và Nam mỗi người thực hiện một thí nghiệm một cách độc lập với nhau. Xác suất thực hiện thành công thí nghiệm của Việt và Nam lẩn lượt là 0,6 và 0,7. Xác suất có đúng một trong hai người thực hiện thành công thí nghiệm biết rằng có ít nhất một người thực hiện thành công thí nghiệm là \(\frac{{\rm{a}}}{{\rm{b}}}\) với \({\rm{a}},{\rm{b}} \in \mathbb{N},{\rm{b}} < 50.\) Giá trị của \({\rm{a}} + {\rm{b}}\) là bao nhiêu?