(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 5)
34 câu hỏi
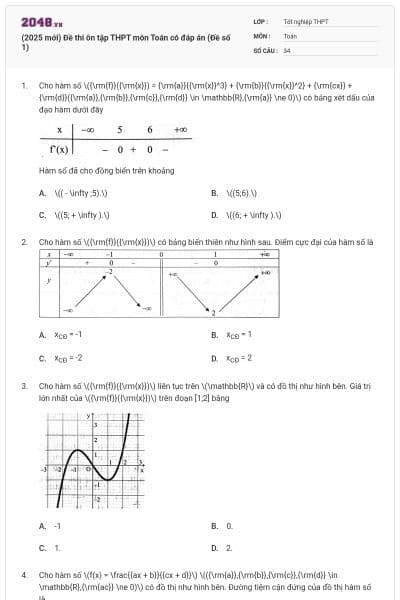
Biết rằng đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}(a,b,c,d \in \mathbb{R})\) ở hình bên có tâm đối xứng là một trong bốn điểm sau đây, điểm đó là điểm nào?
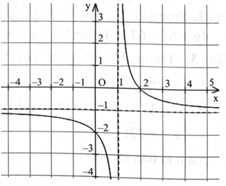
\({\rm{M}}(0; - 1).\)
\({\rm{N}}(1;0).\)
\({\rm{P}}(1; - 1).\)
\({\rm{Q}}( - 1;1).\)
Một trong bốn hình sau đây là đồ thị hàm số \({\rm{y}} = {\log _{\rm{a}}}{\rm{x}}\) với \(0 < {\rm{a}} < 1.\) Hình đó là hình nào?
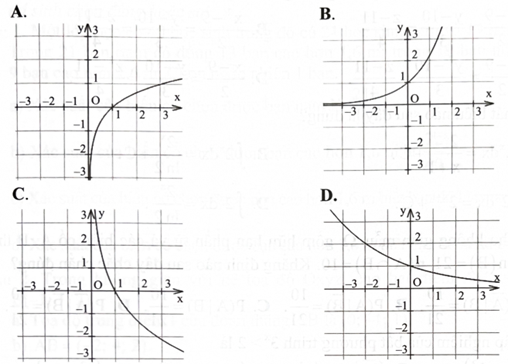
Hình A
Hình B
Hình C
Hình D
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Số đo góc nhị diện \(\left[ {{C^\prime },{\rm{AB}},{\rm{C}}} \right]\) bằng
![Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Số đo góc nhị diện \(\left[ {{C^\prime },{\rm{AB}},{\rm{C}}} \right]\) bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727161807.png)
\({30^o }.\)
\({45^o }.\)
\({60^o }.\)
\({90^o }.\)
Tất cả các nghiệm của phương trình \(\tan x = - \sqrt 3 \) là
\(\frac{{ - \pi }}{3} + {\rm{k}}\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
\(\frac{{ - \pi }}{3} + {\rm{k}}2\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
\(\frac{{ - \pi }}{3} + {\rm{k}}3\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
\(\frac{{ - \pi }}{3} + \frac{{{\rm{k}}\pi }}{2},\forall {\rm{k}} \in \mathbb{Z}.\)
Trong không gian với hệ toạ độ Oxyz, tích vô hướng của hai vectơ \(\overrightarrow {\rm{a}} = (1; - 3;5),\overrightarrow {\rm{b}} = ({\rm{m}};{\rm{n}};{\rm{p}})\) bằng
\(m + 3n + 5p.\)
\(|m - 3n + 5p|.\)
\(\sqrt {{1^2} + {{( - 3)}^2} + {5^2}} \cdot \sqrt {{{\rm{m}}^2} + {{\rm{n}}^2} + {{\rm{p}}^2}} .\)
\(m - 3n + 5p.\)
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình chính tắc của một đường thẳng?
\(\frac{{{\rm{x}} - 9}}{2} = \frac{{{\rm{y}} - 10}}{3} = \frac{{{\rm{z}} - 11}}{4}.\)
\(\frac{{{x^2} - 9}}{2} = \frac{{y - 10}}{3} = \frac{{z - 11}}{4}.\)
\(\frac{{{\rm{x}} - 9}}{2} = \frac{{{{\rm{y}}^2} - 10}}{3} = \frac{{{\rm{z}} - 11}}{4}.\)
\(\frac{{{\rm{x}} - 9}}{2} = \frac{{{\rm{y}} - 10}}{3} = \frac{{{{\rm{z}}^2} - 11}}{4}.\)
Phát biểu nào sau đây là đúng?
\(\int {{2^x}} dx = \frac{{{2^{x + 1}}}}{{x + 1}} + C.\)
\(\int {{2^{\rm{x}}}} {\rm{dx}} = \frac{{{2^{\rm{x}}}}}{{\ln 2}} + C.\)
\(\int {{2^x}} dx = {2^{x + 1}} + C.\)
\(\int {{2^{\rm{x}}}} {\rm{dx}} = \frac{{{2^{\rm{x}}}}}{{\ln 2}}.\)
Cho không gian mẫu \(\Omega \) gồm hữu hạn phần tử và các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{n}}({\rm{B}}) = 21,{\rm{n}}({\rm{A}} \cap {\rm{B}}) = 10.\) Khẳng định nào sau đây chắc chắn đúng?
\({\rm{P}}(\overline {\rm{A}} \mid {\rm{B}}) = \frac{{10}}{{21}}.\)
\({\rm{P}}({\rm{A}}\mid \overline {\rm{B}} ) = \frac{{10}}{{21}}.\)
\({\rm{P}}({\rm{A}}\mid {\rm{B}}) = \frac{{10}}{{21}}.\)
\({\rm{P}}(\overline {\rm{A}} \mid \overline {\rm{B}} ) = \frac{{10}}{{21}}.\)
Tập nghiệm của bất phương trình \({3^x} > 2\) là
\(\left( { - \infty ;{3^2}} \right).\)
\(\left( {{{\log }_3}2; + \infty } \right).\)
\(\left( { - \infty ;{{\log }_3}2} \right).\)
\(\left( {{3^2}; + \infty } \right).\)
Trong không gian với hệ tọa độ Oxyz, mặt cầu tâm \({\rm{I}}(9; - 8;7)\) bán kính 16 có phương trình là
\({({\rm{x}} - 9)^2} + {({\rm{y}} + 8)^2} + {({\rm{z}} - 7)^2} = {16^2}.\)
\({({\rm{x}} - 9)^2} + {({\rm{y}} + 8)^2} + {({\rm{z}} - 7)^2} = 16.\)
\({(x + 9)^2} + {(y - 8)^2} + {(z + 7)^2} = {16^2}.\)
\({(x + 9)^2} + {(y - 8)^2} + {(z + 7)^2} = 16.\)
Nếu hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) thoả mãn \(\int_5^6 f (x)dx = 2,\int_5^7 f (x)dx = 8\) thì \(\int_6^7 f (x)dx\) bằng
16.
6
10.
4.
Xét mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, tứ phân vị thứ hai, tứ phân vị thứ ba lần lượt là 3,6 và 8. Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng
3.
2.
5.
17.
a) Xác suất của biến cố chọn được bạn nam là \(\frac{{21}}{{40}}.\)
b) Xác suất của biến cố chọn được bạn cao hơn \(1,6\;{\rm{m}}\) là \(\frac{{22}}{{40}}.\)
c) Xác suất của biến cố chọn được bạn cao hơn \(1,6\;{\rm{m}}\) biết bạn đó là nam bằng \(\frac{9}{{19}}.\)
d) Xác suất của biến cố chọn được bạn cao hơn \(1,6\;{\rm{m}}\) biết bạn đó là nữ bằng \(\frac{{13}}{{21}}.\)
a) Toạ độ trung điểm I của đoạn thẳng AB là \((0; - 1;1).\)
b) \(\overrightarrow {{\rm{AB}}} = ( - 2;4;2).\)
c) Bán kính đường tròn đường kính AB bằng \(\sqrt {32} .\)
d) Phương trình đường tròn đường kính AB là \({{\rm{x}}^2} + {({\rm{y}} + 1)^2} + {({\rm{z}} - 1)^2} = 32.\)
a) \(f(x) = \frac{{\sin x}}{{\cos x}}.\)
b) \({(\sin x)^\prime } = - \cos x.\)
c) \({(\ln |\sin x|)^\prime } = f(x).\)
d) \(\int f (x)dx = \ln |\sin x| + C.\)
a) \({f^\prime }(x) = \frac{{ad - bc}}{{{{(cx + d)}^2}}}.\)
b) Hàm số nghịch biến trên từng khoảng xác định \(\left( { - \infty ;\frac{{ - {\rm{d}}}}{{\rm{c}}}} \right),\left( {\frac{{ - {\rm{d}}}}{{\rm{c}}}; + \infty } \right).\)
c) Đồ thị hàm số có đường tiệm cận đứng là \({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}\) và đường tiệm cận ngang là \(x = - \frac{d}{c}\)
d) Đồ thị hàm số có tâm đối xứng là \({\rm{I}}\left( {\frac{{ - {\rm{d}}}}{{\rm{c}}};\frac{{\rm{a}}}{{\rm{c}}}} \right).\)
Phương trình \(\log \left( {{x^2} - 2025} \right) = \log x\) có bao nhiêu nghiệm?
Trong không gian với hệ toạ độ Oxyz, mặt phẳng \({\rm{x}} + {\rm{my}} + {\rm{nz}} = 0(\;{\rm{m}},{\rm{n}}\) là các số thực) đi qua hai điểm \({\rm{A}}(2;3;1)\) và \({\rm{B}}(4;1;7).\) Giá trị của \(5\;{\rm{m}} - 6{\rm{n}}\) bằng bao nhiêu?
Một khối rubik có dạng khối tứ diện đều cạnh 4 cm. Xét nhị diện có cạnh chứa một cạnh của khối rubik, hai mặt nhị diện lần lượt chứa hai mặt của rubik có chung cạnh đó. Giả sử số đo nhị diện là \({n^o }\) (làm tròn kết quả đến hàng đơn vị). Giá trị của \(n\) là bao nhiêu?
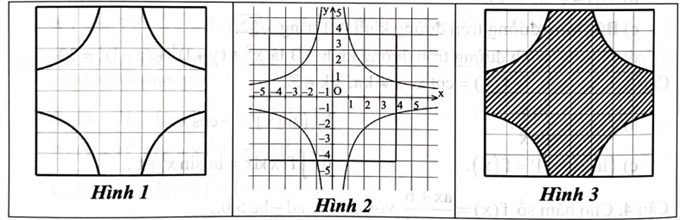
Hoạ sĩ vẽ thiết kế một loại gạch trang trí có dạng như Hình 1, gạch có dạng hình vuông cạnh 8 dm. Khi đặt bản vẽ trong hệ tọa độ Oxy với đơn vị của mỗi trục là 1 dm thì mối nét cong phía trong thuộc một trong hai đường hypebol \({\rm{y}} = - \frac{4}{{\rm{x}}},{\rm{y}} = \frac{4}{{\rm{x}}}\) (Hình 2); các cạnh của viên gạch lần lượt thuộc 4 đường thẳng \({\rm{x}} = - 4,{\rm{x}} = 4,{\rm{y}} = - 4,{\rm{y}} = 4.\) Người ta sơn màu hồng vào phần hình được gạch chéo như Hình 3. Diện tích phần sơn màu hồng là bao nhiêu \({\rm{d}}{{\rm{m}}^2}\) (làm tròn kết quả đến hàng phần mười)?
Bác Hùng có kế hoạch dùng hết \(20\;{{\rm{m}}^2}\) kính để làm một bể cá có dạng hình hộp chữ nhật không nắp, chiều dài gấp ba chiều rộng (các mối ghép không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu \({{\rm{m}}^3}\) (làm tròn kết quả đến hàng phần mười)?
Bạn An chọn ngẫu nhiên 6 đỉnh trong 2025 đỉnh của một đa giác đều. Sau đó bạn Bình chọn ngẫu nhiên 3 đỉnh trong 6 đỉnh An vừa chọn. Xác suất của biến cố tam giác có 3 đỉnh được Bình chọn không có điểm chung nào với tam giác có 3 đỉnh là 3 điểm còn lại trong 6 điểm được An chọn là bao nhiêu?