(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
34 câu hỏi
Cho hàm số \({\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + {\rm{d}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R},{\rm{a}} \ne 0)\) có bảng xét dấu của đạo hàm dưới đây
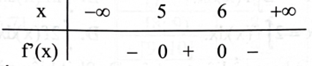
Hàm số đã cho đồng biến trên khoảng
\(( - \infty ;5).\)
\((5;6).\)
\((5; + \infty ).\)
\((6; + \infty ).\)
Cho hàm số \({\rm{f}}({\rm{x}})\) có bảng biến thiên như hình sau. Điểm cực đại của hàm số là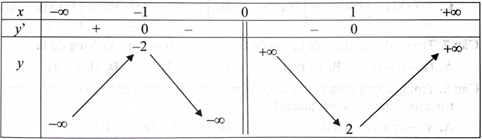
xCĐ = -1
xCĐ = 1
xCĐ = -2
xCĐ = 2
Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng
![Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727150158.png)
-1
0.
1.
2.
Cho hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\) \(({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R},{\rm{ac}} \ne 0)\) có đồ thị như hình bên. Đường tiệm cận đứng của đồ thị hàm số là
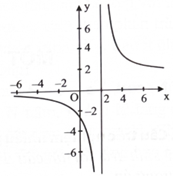
\({\rm{y}} = - 2.\)
\({\rm{y}} = 2.\)
\({\rm{x}} = - 2.\)
\({\rm{x}} = 2.\)
Cho \({\rm{f}}({\rm{x}})\) là hàm số liên tục trên \(\mathbb{R}.\) Phát biểu nào sau đây là đúng?
\(\int 2 f(x)dx = - 2\int f (x)dx.\)
\(\int 2 f(x)dx = 2 + \int f (x)dx.\)
\(\int 2 f(x)dx = 2\int f (x)dx.\)
\(\int 2 f(x)dx = 2 - \int f (x)dx.\)
Cho \({\rm{f}}({\rm{x}})\) là hàm số liên tục trên \(\mathbb{R}.\) Phát biểu nào sau đây là đúng?
\(\int_3^4 f (x)dx \cdot \int_4^5 f (x)dx = \int_3^5 f (x)dx\)
\(\int_3^4 f (x)dx - \int_4^5 f (x)dx = \int_3^5 f (x)dx.\)
\(\int_3^4 f (x)dx + \int_4^5 f (x)dx = \int_5^3 f (x)dx.\)
\(\int_3^4 f (x)dx + \int_4^5 f (x)dx = \int_3^5 f (x)dx.\)
Trong không gian với hệ tọa độ Oxyz, vectơ \(\overrightarrow {\rm{u}} = \overrightarrow {\rm{i}} - \overrightarrow {\rm{j}} - \overrightarrow {\rm{k}} \) có tọa độ là
\((1; - 1; - 1).\)
\((1;1;1).\)
\((1; - 1;1).\)
\((1;1; - 1).\)
Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình tổng quát của mặt phẳng?
\({x^2} - 4y + 5z - 6 = 0\)
\(3x - {y^4} + 5z - 6 = 0.\)
\(3x - 4y + 5z - 6 = 0.\)
\(3x - 4y + {z^5} - 6 = 0.\)
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình của mặt cầu?
\( - {(x - 1)^2} + {(y + 1)^2} + {(z - 10)^2} = 225.\)
\({({\rm{x}} - 1)^2} - {({\rm{y}} + 1)^2} + {({\rm{z}} - 10)^2} = 225.\)
\({({\rm{x}} - 1)^2} + {({\rm{y}} + 1)^2} - {({\rm{z}} - 10)^2} = 225.\)
\({({\rm{x}} - 1)^2} + {({\rm{y}} + 1)^2} + {({\rm{z}} - 10)^2} = 225.\)
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng?
\(\frac{{x - 9}}{3} = \frac{{y - 1}}{{11}} = \frac{{z + 7}}{{14}}.\)
\(\frac{{x - 1}}{{4y}} = \frac{{y - 2}}{5} = \frac{{z + 3}}{6}.\)
\(\frac{{{\rm{x}} + 7}}{{10}} = \frac{{{\rm{y}} + 8}}{{11{\rm{z}}}} = \frac{{{\rm{z}} + 9}}{{12}}.\)
\(\frac{{{\rm{x}} - 13}}{{16}} = \frac{{{\rm{y}} - 14}}{{17}} = \frac{{{\rm{z}} - 15}}{{18{\rm{z}}}}.\)
Cho các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,2;{\rm{P}}({\rm{B}}) = 0,4.\) Xác suất của biến cố A với điều kiện B bằng
0,2.
0,08.
0,6.
0,5.
Khi thống kê kết quả thi thử của 100 học sinh ở một trung tâm giáo dục, người ta được bảng thống kê tần số ghép nhóm như hình bên. Số trung bình của mẫu số liệu là
Điểm | Giá trị đại diện | Tần số |
\([3;4)\) | 3,5 | 2 |
\([4;5)\) | 4,5 | 7 |
\([5;6)\) | 5,5 | 21 |
\([6;7)\) | 6,5 | 26 |
\([7;8)\) | 7,5 | 29 |
\([8;9)\) | 8,5 | 12 |
[9 ; 10] | 9,5 | 3 |
|
| n = 100 |
6,73.
6,7.
6,72.
6,71.
a) Đường thẳng \(\Delta \) có một vectơ chỉ phương với tọa độ là \((1;1;\sqrt 2 ).\)
b) Mặt phẳng \(({\rm{P}})\) có một vectơ pháp tuyến với toạ độ là \((1;1; - \sqrt 2 ).\)
c) Tích vô hướng của hai vectơ \(\overrightarrow {\rm{u}} (1; - 1;\sqrt 2 ),\overrightarrow {\rm{v}} (1;1; - \sqrt 2 )\) bằng \(\frac{{ - 1}}{2}.\)
d) Góc giữa đường thẳng \(\Delta \) và mặt phẳng \(({\rm{P}})\) là \({60^o }.\)
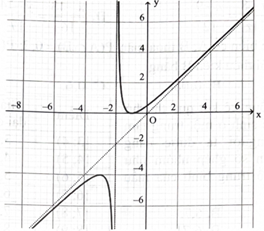
a) Đạo hàm của hàm số là \({{\rm{f}}^\prime }({\rm{x}}) = 1 - \frac{1}{{{{({\rm{x}} + 2)}^2}}}.\)
b) \({{\rm{f}}^\prime }({\rm{x}}) < 0 \Leftrightarrow {\rm{x}} \in ( - 3; - 2) \cup ( - 2; - 1),{{\rm{f}}^\prime }({\rm{x}}) > 0 \Leftrightarrow {\rm{x}} \in ( - \infty ; - 3) \cup ( - 1; + \infty ).\)
c) Đồ thị hàm số có đường tiệm cận xiên là \(x = - 2\) và đường tiệm cận đứng là \(y = x.\)
d) Hàm số đã cho có đồ thị như hình sau:
a) Xác suất của biến cố chọn được học sinh bị tật khúc xạ là \(\frac{{89}}{{240}}.\)
b) Xác suất của biến cố chọn được học sinh nữ là \(\frac{{132}}{{240}}.\)
c) Xác suất của biến cố chọn được học sinh bị tật khúc xạ, biết học sinh đó là nữ bằng \(\frac{{47}}{{89}}.\)
d) Xác suất của biến cố chọn được học sinh nữ, biết học sinh đó bị tật khúc xạ bằng \(\frac{{47}}{{132}}.\)
a) Hoành độ giao điểm của \(({\rm{P}})\) và Ox là -2 và 2.
b) \(\int {\left( {{x^2} - 4} \right)} dx = \frac{{{x^3}}}{3} + 4x + C.\)
c) \(\left| {{x^2} - 4} \right| = {x^2} - 4\forall x \in [ - 2;2]\)
d) Diện tích hình phẳng giới hạn bởi \(({\rm{P}})\) và Ox bằng \(\frac{{32}}{3}.\)
Cho hình chóp đều \({\rm{S}}.{\rm{ABCD}}\) có tất cả các cạnh bằng nhau. Góc giữa đường thẳng SA và mặt phẳng ABCD là \({{\rm{n}}^o }\) với n là số thực. Giá trị của n bằng bao nhiêu?
Phương trình \({\log _3}\left( {{x^2} - 3x - 5} \right) = {\log _3}x\) có bao nhiêu nghiệm?
Người ta thả một số lá bèo vào một hồ nước. Sau 10 giờ, số lượng lá bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, số lượng lá bèo tăng gấp 10 lần số lượng lá bèo trước đó và tốc độ tăng không đổi. Sau ít nhất mấy giờ thì số lá bèo phủ kín hơn một phần tư hồ (làm tròn kết quả đến hàng đơn vị)?
Người ta cần làm một khối thuỷ tinh có dạng hình chóp tứ giác đều có diện tích toàn phần bằng \(8{\rm{d}}{{\rm{m}}^2}.\) Cạnh đáy của hình chóp bằng bao nhiêu decimét để thể tích của khối thuỷ tinh lớn nhất (làm tròn kết quả đến hàng phần trăm)?
Một vật thể có dạng khối tròn xoay được tạo thành khi quay hình phẳng D quanh trục \(\Delta \) một vòng, biết rằng:
i) Hình phẳng D giới hạn bởi một parabol \(({\rm{P}})\) và đường thẳng a.
ii) Đường thẳng a vuông góc với đường thẳng \(\Delta \) là trục đối xứng của parabol \(({\rm{P}}).\)
iii) Đường thẳng a cắt parabol \(({\rm{P}})\) tại hai điểm có khoảng cách 6 dm, khoảng cách từ đỉnh của \(({\rm{P}})\) đến \(\Delta \) bằng 3 dm.
Thể tích của vật thể bằng bao nhiêu \({\rm{d}}{{\rm{m}}^3}\) (làm tròn kết quả đến hàng phần mười)?
Một hộp chứa 15 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 15. Bạn An lấy ra lần lượt 3 thẻ từ hộp. Thẻ lấy ra không được hoàn lại hộp. Tính xác suất của biến cố: "Lần thứ ba An lấy được thẻ ghi số lẻ, biết rằng lần hai An lấy được thẻ ghi số chẵn" (làm tròn kết quả đến hàng phần trăm).