(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 3)
34 câu hỏi
Trong các hình dưới đây, có một hình là đồ thị của hàm số \({\rm{y}} = {{\rm{a}}^{\rm{x}}}(0 < {\rm{a}} < 1)\), hình đó là hình nào?
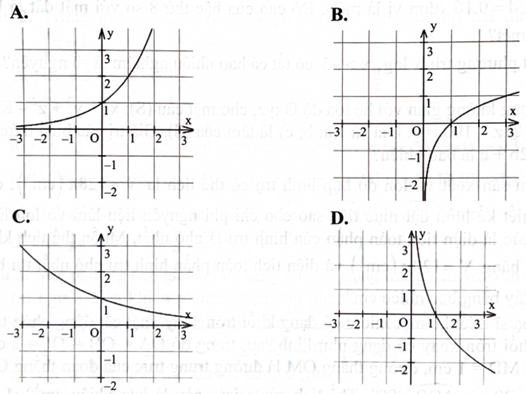
Hình A
Hình B
Hình C
Hình D
Trong không gian với hệ toạ độ Oxyz, toạ độ của vectơ \(\vec u = 3\vec i - \vec j - 2\vec k\) là
\((3; - 1; - 2).\)
\((3;1; - 2).\)
\((3; - 1;2).\)
\((3;1;2).\)
Nếu hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có một nguyên hàm là hàm số \({\rm{y}} = {\rm{F}}({\rm{x}})\) thì giá trị của biểu thức \(\int_5^3 {\rm{f}} ({\rm{x}}){\rm{dx}}\) bằng
\(F(5) - F(3).\)
\(F(3) - F(5).\)
\(F(3).\) \(F(5).\)
\(F(3):F(5).\)
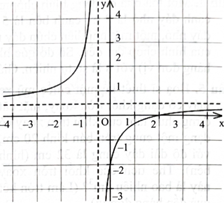
Nếu hàm số \(y = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}}\), \({\rm{n}} \in \mathbb{R}\) ) có đồ thị như hình bên thì có điểm cực tiểu là
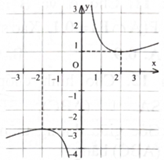
1.
-1.
2.
-2.
Đạo hàm của hàm số \({\rm{f}}({\rm{x}}) = \cos 5{\rm{x}}\) là
\({\rm{f}}({\rm{x}}) = 5\sin 5{\rm{x}}.\)
\(f(x) = - \sin 5x.\)
\({\rm{f}}({\rm{x}}) = \sin 5{\rm{x}}.\)
\(f(x) = - 5\sin 5x.\)
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm \({\rm{M}}({\rm{a}};{\rm{b}};{\rm{c}})\) và nhận \(\vec n = (2; - 3;4)\) là vectơ pháp tuyến có phương trình là
\(a(x - 2) + b(y + 3) + c(z - 4) = 0.\)
\(2(x - a) - 3(y - b) + 4(z - c) = 0.\)
\(a(x - 2) + b(y - 3) + c(z - 4) = 0.\)
\(2(x - a) + 3(y - b) + 4(z - c) = 0.\)
Trong không gian với hệ tọa độ Oxyz, nếu \(\varphi \) là góc giữa đường thẳng \(\frac{{{\rm{x}} - {\rm{x}}0}}{{\rm{a}}} = \frac{{{\rm{y}} - {\rm{y}}0}}{{\;{\rm{b}}}} = \frac{{{\rm{z}} - {{\rm{z}}_0}}}{{\rm{c}}}\) và mặt phẳng \({\rm{Ax}} + {\rm{By}} + {\rm{Cz}} + {\rm{D}} = 0\) thì giá trị của biểu thức \(\frac{{|{\rm{aA}} + {\rm{bB}} + {\rm{cC}}|}}{{\sqrt {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \cdot \sqrt {{{\rm{A}}^2} + {{\rm{B}}^2} + {{\rm{C}}^2}} }}\) bằng
\(\cos \varphi .\)
\(\tan \varphi .\)
\(\cot \varphi .\)
\(\sin \varphi .\)
Trong không gian với hệ toạ độ Oxyz mặt cầu \({({\rm{x}} - 5)^2} + {({\rm{y}} + 8)^2} + {({\rm{z}} - 13)^2} = {9^2}\) có toạ độ tâm là
\((5;8;13).\)
\((5; - 8;13).\)
\(( - 5;8; - 13).\)
\(( - 5; - 8; - 13).\)
Phát biểu nào sau đây là đúng?
\(\int 1 {2^{\rm{x}}}{\rm{dx}} = {12^{\rm{x}}}.\)
\(\int 1 {2^{\rm{x}}}{\rm{dx}} = \frac{{{{12}^{\rm{x}}}}}{{\ln 12}}.\)
\(\int 1 {2^{\rm{x}}}{\rm{dx}} = \frac{{{{12}^{\rm{x}}}}}{{\ln 12}} + \) C.
\(\int 1 {2^{\rm{x}}}{\rm{dx}} = {12^{\rm{x}}} + \) C.
Khi thống kê chiều cao (đơn vị là cm ) học sinh của lớp 12 A, người ta sử dụng mẫu số liệu ghép nhóm và được một kết quả cho bởi Bảng 1. Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng
Nhóm | Tần số |
\([155;160)\) | 2 |
\([160;165)\) | 5 |
\([165;170)\) | 21 |
\([170;175)\) | 11 |
\([175;180)\) | 1 |
| \({\rm{n}} = 40\) |
25.
5.
20.
180.
Cho A và B là hai biến cố thoả mãn \({\rm{P}}({\rm{A}}) = 0,6,{\rm{P}}({\rm{B}}) = 0,2\) và \({\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,1.\) Xác suất \({\rm{P}}({\rm{A}} \cup {\rm{B}})\) bằng
0,9.
0,012.
0,8.
0,7.
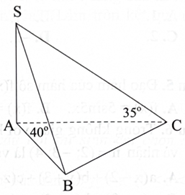
Cho hình chóp S.ABC thoả mãn \({\rm{SA}} \bot ({\rm{ABC}}),\widehat {{\rm{SBA}}} = {40^o },\widehat {{\rm{SCA}}} = {35^o }.\)
Góc giữa đường thẳng SB và mặt phẳng \(({\rm{ABC}})\) bằng
\({40^o }.\)
\({35^o }.\)
\({50^o }.\)
\({55^o }.\)
a) Mặt phẳng \(\left( {{{\rm{P}}_1}} \right)\) có một vectơ pháp tuyến với tọa độ là \((3;4;7).\)
b) Mặt phẳng \(\left( {{{\rm{P}}_2}} \right)\) có một vectơ pháp tuyến với tọa độ là \((5;12;17).\)
c) Tích vô hướng của hai vectơ với tọa độ \((3;4;0)\) và \((5;0;12)\) bằng 15.
d) Góc giữa hai mặt phẳng \(\left( {{{\rm{P}}_1}} \right)\) và \(\left( {{{\rm{P}}_2}} \right)\) (làm tròn đến hàng đơn vị của độ) bằng \({77^o }.\)
a) \(\int_0^1 8 f(x)dx = 8\int_0^1 g (x)dx.\)
b) \(\int_0^1 3 g(x)dx = 3\int_0^1 g (x)dx \ne 3\int_0^1 f (x)dx.\)
c) \(\int_0^1 {(8f(} x) - 3g(x))dx = \int_0^1 8 f(x)dx - 3\int_0^1 g (x)dx\)
d) \(\int_0^1 {(8f(} x) - 3g(x))dx = 8 \cdot 2 - 5 \cdot 3 = 1.\)
a) Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - \frac{1}{2}} \right\}\)
b) Đạo hàm của hàm số là \({y^\prime } = \frac{5}{{{{(2x + 1)}^2}}}\)
c) Các đường tiệm cận của hàm số là \({\rm{x}} = \frac{1}{2},{\rm{y}} = - \frac{1}{2}.\)
d) Đồ thị của hàm số có dạng như hình bên.
a) \({\rm{P}}({\rm{A}}) = \frac{{22}}{{45}}.\)
b) \({\rm{P}}({\rm{B}}) = \frac{{28}}{{45}}.\)
c) \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = \frac{{10}}{{22}}.\)
d) \({\rm{P}}({\rm{B}}\mid \overline {\rm{A}} ) = \frac{7}{{17}}.\)
Tập nghiệm của phương trình \(\sin x = \frac{1}{3}\) là \(a + k2\pi ,b + k2\pi \mid k \in \mathbb{Z}\) với a, b là các hằng số dương thuộc \((0;\pi ).\) Giá trị của biểu thức \(\frac{{{\rm{a}} + {\rm{b}}}}{\pi }\) là bao nhiêu?
Một người gửi ngân hàng 40 triệu đồng theo thể thức lãi kép với lãi suất 0,52% một tháng (kể từ tháng thứ hai, tiền lãi được tính theo phần trăm của tổng tiền lãi tháng trước đó và tiền gốc của tháng trước đó). Giả sử lãi suất không thay đổi trong nhiều tháng liên tiếp. Sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 48 triệu đồng?
Một cái bánh ít lá gai có dạng hình chóp tứ giác đều với cạnh đáy là 4 cm và cạnh bên là 6 cm. Thể tích của cái bánh này bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\)? (Làm tròn kết quả đến hàng đơn vị)

Một toà nhà có dạng hình chóp cụt tứ giác đều với cạnh đáy lớn là 14 m, cạnh đáy nhỏ là 8 m, cạnh bên là 5 m. Xét góc nhị diện có cạnh chứa cạnh đáy nhỏ, một mặt nhị diện chứa đáy nhỏ và mặt nhị diện còn lại chứa mặt bên của hình chóp cụt đều. Số đo góc nhị diện đó bằng \({{\rm{n}}^o }\) (làm tròn kết quả đến hàng đơn vị) với n là số tự nhiên. Giá trị của n là bao nhiêu?
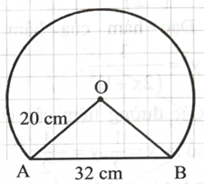
Hoạ sĩ thiết kế một chiếc mũ xe máy có dạng khối tròn xoay, mặt cắt đứng chứa tâm của khối tròn xoay có dạng một cung tròn bán kính 20 cm, với độ dài dây cung là 32 cm (hình bên). Thể tích của khối tròn xoay này là bao nhiêu \({\rm{d}}{{\rm{m}}^3}\) ? (Làm tròn kết quả đến hàng đơn vị)
Một phân xưởng sản xuất bóng đèn có tỉ lệ bóng đạt chuẩn là 95%. Để hạn chế số lượng bóng không đạt chuẩn được bán ra thị trường, người ta lắp đặt một thiết bị kiểm tra chất lượng tự động S. Nếu một bóng đèn không đạt chuẩn, thiết bị S sẽ loại bỏ nó với xác suất 0,99. Khi kiểm tra lại các bóng đèn bị loại, người ta nhận thấy có 10% số đó là bóng đạt chuẩn. Chọn ngẫu nhiên 1 bóng đèn do phân xưởng đó sản xuất. Xác suất bóng đèn được chọn đạt chuẩn biết rằng nó không bị thiết bị S loại bỏ bằng \(\frac{{\rm{a}}}{{\rm{b}}}\) với a, b là số nguyên dương và \({\rm{b}} < 2000.\) Giá trị của biểu thức \({\rm{a}} + {\rm{b}}\) là bao nhiêu?