Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 49)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
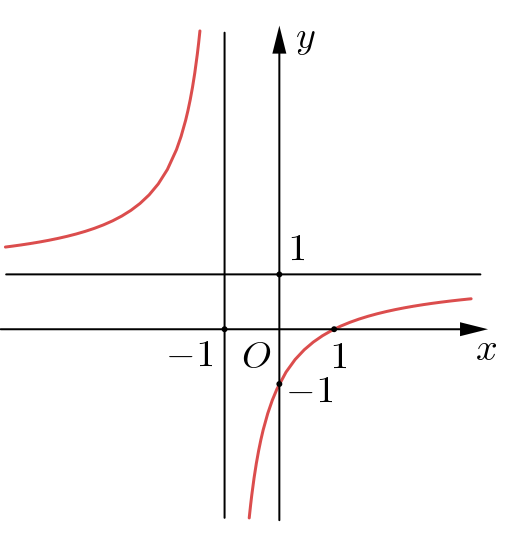
Biểu thức \[f\left( x \right)\] là biểu thức nào sau đây?
\[x + \frac{1}{x}\].
\[ - {x^3} + 3x - 1\].
\[{x^3} - 1\].
\[\frac{{x - 1}}{{x + 1}}\].
Cho hàm số \[f\left( x \right)\] liên tục trên \[\left[ { - 1;5} \right]\] và có đồ thị trên đoạn \[\left[ { - 1;5} \right]\] như hình vẽ dưới.
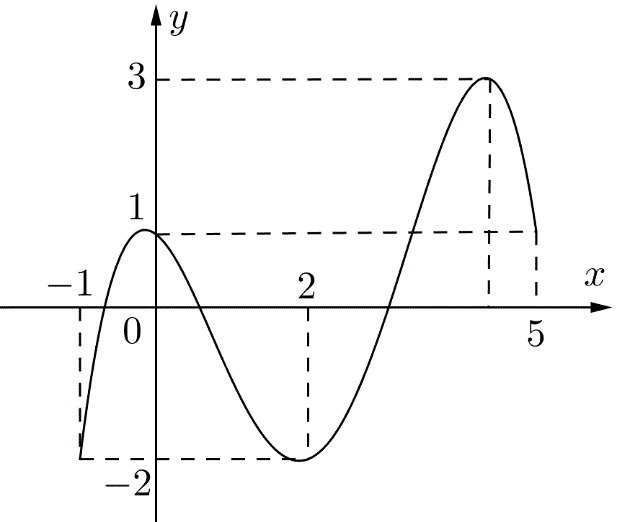
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[f\left( x \right)\] trên đoạn \[\left[ { - 1;5} \right]\]bằng
\[4\].
\[1\].
\[2\].
\[ - 1\].
Trong không gian \[Oxyz\], đường thẳng đi qua điểm \[A\left( {1;1;1} \right)\] và vuông góc với mặt phẳng tọa độ \[\left( {Oxy} \right)\]có phương trình tham số là
\[\left\{ \begin{array}{l}x = 1\\y = 1\\z = 1 + t\end{array} \right.\].
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1 + t\\z = 1\end{array} \right.\].
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1\\z = 1\end{array} \right.\].
\[\left\{ \begin{array}{l}x = 1\\y = 1 + t\\z = 1\end{array} \right.\].
Đường thẳng \[2y + 1 = 0\] là tiệm cận ngang của đồ thị hàm số nào sau đây?
\[y = \frac{{3 - {x^2}}}{{2{x^2} - 3x + 1}}\].
\[y = \frac{{{x^2} + x + 1}}{{1 - 2x}}\].
\[y = \frac{{x + 1}}{{2x + 1}}\].
\[y = \frac{{2x + 1}}{{1 - x}}\].
Cho hai biến cố \(A\) và \(B\), với \(P\left( B \right) = 0,8\);\(P\left( {A|B} \right) = 0,7\);\(P\left( {A|\overline B } \right) = 0,45\). Tính \(P\left( {B|A} \right)\).
\(0,65\).
\(0,25\).
\(0,5\).
\(\frac{{56}}{{65}}\).
Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình.
Thời gian (phút) | \[\left[ {10;15} \right)\] | \[\left[ {15;20} \right)\] | \[\left[ {20;25} \right)\] | \[\left[ {25;30} \right)\] | \[\left[ {30;35} \right)\] |
Số ngày tập của Hưng | \[2\] | \[14\] | \[8\] | \[3\] | \[3\] |
Số ngày tập của Bình | \[12\] | \[8\] | \[7\] | \[3\] | \[0\] |
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập của Hưng và Bình lần lượt là
\[20\]phút và \[25\]phút.
\[25\]phút và \[20\]phút.
\[20\]phút và \[20\]phút.
\[25\]phút và \[25\]phút.
Trong không gian \(Oxyz\), phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;2;1} \right)\) và đi qua điểm \(A\left( {0;4; - 1} \right)\)là
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 3\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\).
Trong không gian \(Oxyz\), một vectơ pháp tuyến của mặt phẳng \(\frac{x}{{ - 2}} + \frac{y}{{ - 1}} + \frac{z}{3} = 1\) là
\(\overrightarrow n = \left( { - 3; - 6; - 2} \right)\).
\(\overrightarrow n = \left( { - 2; - 1;3} \right)\).
\(\overrightarrow n = \left( {2; - 1;3} \right)\).
\(\overrightarrow n = \left( {3;6; - 2} \right)\).
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục \[Ox\]tại \[x = 1\] và \[x = 2\]. Một mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\]\[\left( {1 \le x \le 2} \right)\] cắt vật thể đó có diện tích \[S\left( x \right) = 2026x\]. Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
\(1518\pi \).
\(3039\).
\(3039\pi \).
\(3036\).
Tìm tất cả nguyên hàm \[F\left( x \right)\] của hàm số \[f\left( x \right) = x - \frac{1}{x}\].
\(\frac{1}{2}{x^2} - \ln \left| x \right|\).
\(\frac{1}{2}{x^2} - \ln \left| x \right| + C\).
\(\frac{1}{2}{x^2} - \ln x + C\).
\(1 - \ln \left| x \right| + C\).
Trong không gian với hệ tọa độ \[Oxyz\], cho mặt phẳng \[\left( P \right):6x + 8y + 10z - 1 = 0\] và đường thẳng \[d:\frac{{x - 2}}{3} = \frac{{y + 1}}{4} = \frac{{z - 5}}{5}\]. Góc giữa đường thẳng \[d\] và mặt phẳng \[\left( P \right)\] là
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} = 6\) và công bội \(q = - \frac{1}{2}\). Tính \({u_5}\).
\(\frac{3}{8}\).
\( - 3\).
\( - \frac{3}{8}\).
\( - \frac{4}{3}\).
a) Đồ thị \[\left( {{C_m}} \right)\] luôn có hai điểm cực trị.
b) Hàm số \[f\left( x \right)\]có hai điểm cực trị khi \[m > 6\].
c) Khi \[m = 5\] thì hàm số \[f\left( x \right)\] đồng biến trên khoảng \[\left( {3; + \infty } \right)\].
d) Hàm số \[f\left( x \right)\]nghịch biến trên \[\mathbb{R}\].
a) Hàm số \(h\left( t \right)\) có công thức là \(h\left( t \right) = - 0,005{t^4} + 0,1{t^3}\).
b) Giai đoạn tăng trưởng của cây đậu Hà Lan đó kéo dài \(15\) tuần.
c) Chiều cao tối đa của cây đậu Hà Lan đó là \(88\) centimet.
d) Vào thời điểm cây đậu Hà Lan phát triển nhanh nhất thì chiều cao của cây là \(53\) centimet.
a) Xác suất chọn được viên bi màu vàng có đánh số bằng 18,57%.
b) Xác suất chọn được viên bi màu đỏ bằng 62,5%.
c) Xác suất chọn được viên bi không đánh số bằng 43,75%.
d) Giả sử viên bi được lấy ra là viên bi chưa được đánh số, xác suất để viên bi đó là bi đỏ thấp hơn xác suất viên bi đó là bi vàng.
a) Điểm \[B\] thuộc mặt phẳng \[\left( P \right)\].
b) Hình chiếu vuông góc của A trên mặt phẳng \[\left( {Oxz} \right)\]là \[H\left( {1;0;6} \right)\].
c) Góc giữa đường thẳng \[AB\] và mặt phẳng \[\left( P \right)\](làm tròn đến hàng đơn vị) là \[50^\circ \].
d) Giả sử viên đạn chuyển động thẳng đều theo hướng vectơ \[\vec v = \left( { - 1;4; - 10} \right)\]với vận tốc \[850\,{\rm{m/s}}\] (bỏ qua mọi lực cản và chướng ngại vật) sau hai phút viên đạn bắn ra đi qua điểm \[B\].
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Nhà máy \(A\) chuyên sản xuất một loại sản phẩm cho nhà máy \(B\). Hai nhà máy thoả thuận rằng, hàng tháng nhà máy \(A\) cung cấp cho nhà máy \(B\) số lượng sản phẩm theo đơn đặt hàng của nhà máy \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(x\) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(p\left( x \right) = 90 - 0,01{x^2}\) (đơn vị: triệu đồng). Chi phí để nhà máy \(A\) sản xuất \(x\) tấn sản phẩm trong một tháng là \(C\left( x \right) = \frac{1}{2}\left( {200 + 27x} \right)\) (đơn vị: triệu đồng), thuế giá trị gia tăng mà nhà máy \(A\) phải đóng cho nhà nước là \(10\% \) tổng doanh thu mỗi tháng. Hỏi nhà máy \(A\) bán cho nhà máy \(B\) bao nhiêu tấn sản phẩm để mỗi tháng thu được lợi nhuận (sau khi đã trừ thuế giá trị gia tăng) cao nhất?
Bánh Taco là một món ăn đặc trưng của Mexico, bánh Taco được tạo thành từ một chiếc bánh Tortilla (bánh ngô) cuộn quanh thức ăn. Cụ thể, để làm một chiếc bánh Taco ta lấy bánh Tortilla tròn có đường kính 20 cm đặt vào mặt trong của hình trụ có bán kính \(R = 4\) cm, dọc theo đường kính của Tortilla và gấp bánh lại quanh hình trụ. Sau đó ta sẽ đổ đầy thịt, phô mai, và rau củ đến tận mép bánh. Gọi \(x\) là khoảng cách từ tâm bánh Tortilla đến một điểm P trên đường kính (tham khảo hình vẽ).
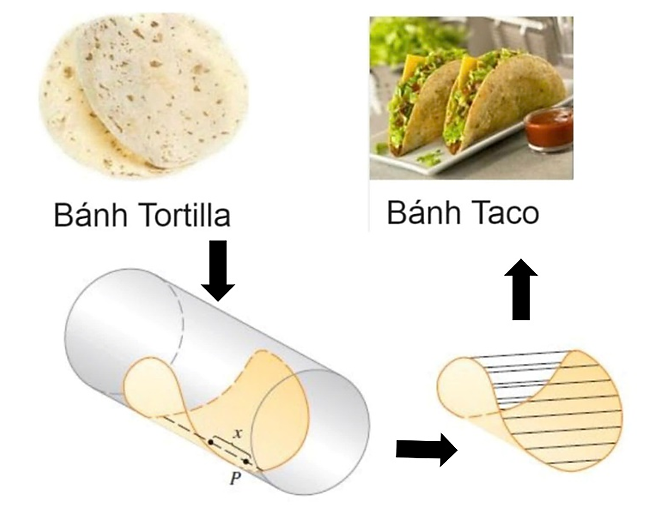
Tính thể tích của bánh Taco theo đơn vị centimet khối (kết quả làm tròn đến hàng đơn vị).
Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi học sinh giỏi, có 10 bạn trong đội tuyển gồm 2 bạn đến từ lớp 12A, 3 bạn từ lớp 12B, 5 bạn còn lại đến từ 5 lớp khác (mỗi lớp một bạn). Thầy giáo xếp ngẫu nhiên các bạn kể trên ngồi vào một bàn dài có 10 ghế mà mỗi bên có 5 ghế xếp đối diện nhau. Tính xác suất để không có học sinh nào cùng lớp ngồi đối diện nhau (làm tròn kết quả đến hàng phần mười).
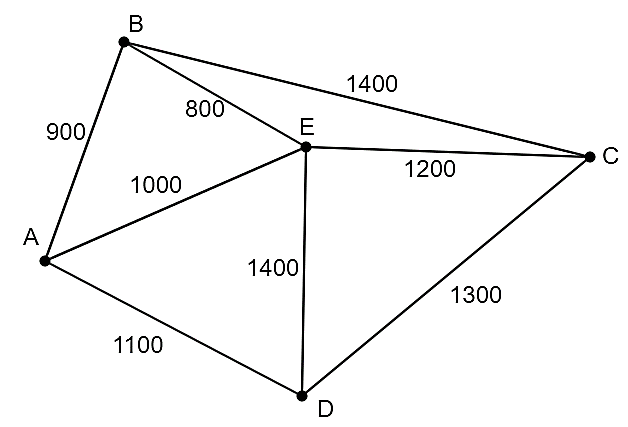
Một công ty vận tải cần giao hàng đến tất cả các thành phố \(A\), \(B\), \(C\), \(D\), \(E\) (hình vẽ). Chi phí di chuyển giữa các thành phố được mô tả trên hình (tính theo đơn vị nghìn đồng). Xe giao hàng của công ty xuất phát từ thành phố \(A\)đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố \(A\). Tìm chi phí thấp nhất của xe giao hàng (tính theo đơn vị nghìn đồng)?
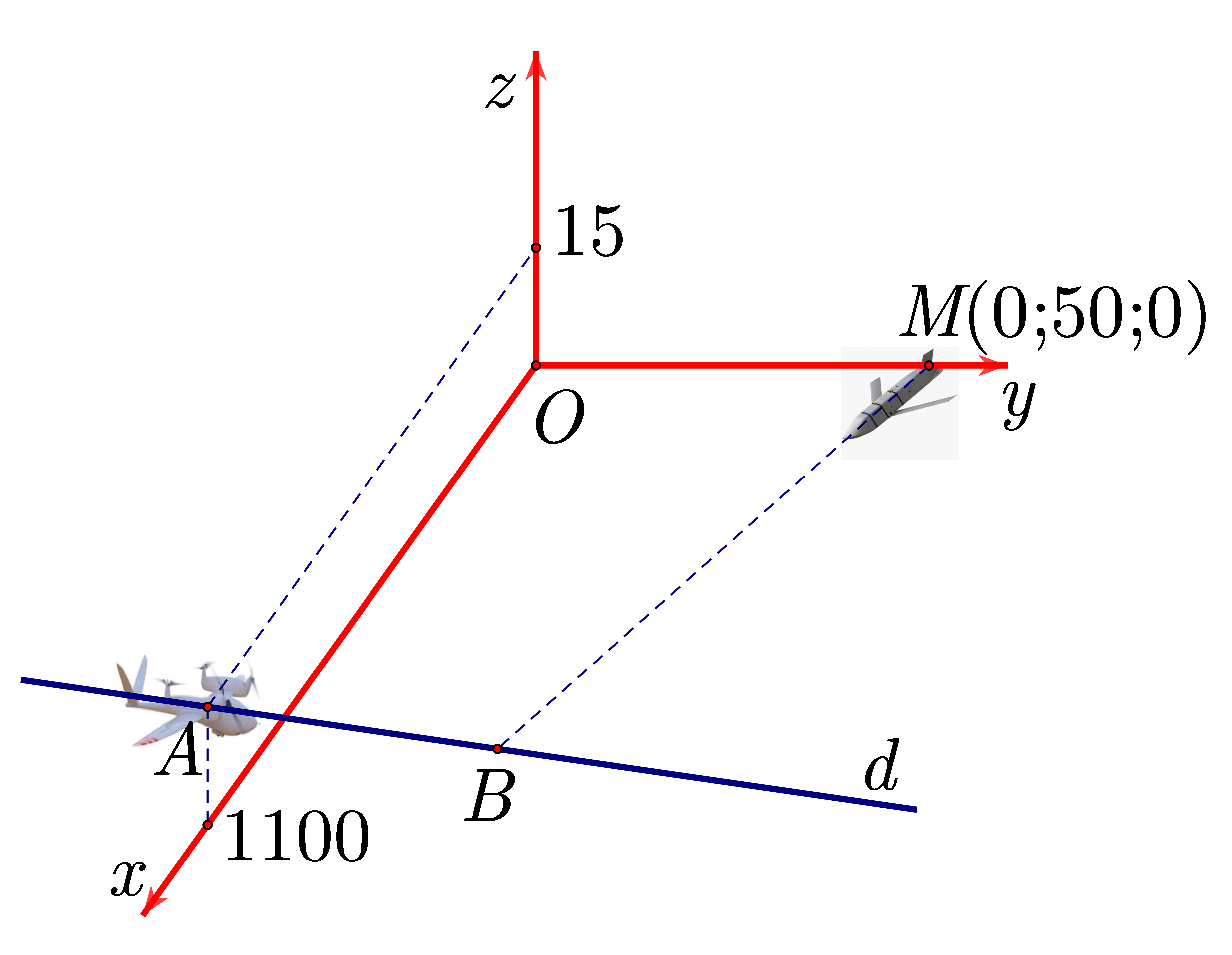
Trong không gian với hệ trục tọa độ \[Oxyz,\] xét mô hình phòng không như sau: rada đặt tại gốc tọa độ \[O\left( {0\,;0\,;0} \right)\], tên lửa phòng không đặt tại điểm \[M\left( {0\,;50\,;0} \right)\], mỗi đơn vị tương ứng với \[10\,\,{\rm{m}},\] mặt phẳng \[\left( {Oxy} \right)\] trùng với mặt đất, trục \[Oz\] vuông góc mặt đất và hướng lên. Giả sử mọi UAV (phương tiện bay không người lái) và tên lửa đều chuyển động thẳng đều. Tại thời điểm \[t = 0\,\,({\rm{s)}},\] rada phát hiện ra UAV \[A\] ở toạ độ \[{A_0}\left( {1100\,;0\,;15} \right)\]. Tại thời điểm \[t = 1\,\,{\rm{(s)}},\] rađa theo dõi thấy UAV \[A\] ở tọa độ \[{A_1}\left( {1095\,;1\,;14,5} \right)\] trên đường thẳng \[d\]. Tại thời điểm \[t = 6\,\,{\rm{(s)}},\] một tên lửa được phóng lên và chuyển động thẳng đều với vận tốc \[1300\,\,{\rm{(m/s)}},\] va chạm và phá huỷ UAV \[A\] tại điểm \[B\] trên \[d\]. Hỏi sau bao nhiêu giây kể từ lúc được phóng lên thì tên lửa va chạm với UAV (làm tròn kết quả đến hàng phần trăm của giây)?
Cho hình hộp chữ nhật \[ABCD.A'B'C'D'\]. Biết khoảng cách từ đỉnh \[A\] tới mặt phẳng\[\left( {A'BD} \right)\] bằng \[10\]. Tính thể tích nhỏ nhất của khối hộp chữ nhật \[ABCD.A'B'C'D'\] (làm tròn kết quả đến hàng đơn vị).