Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 48)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + 2\) là:
\(2x + C\).
\(3{x^2} + 2x + C\).
\({x^3} + 2x + C\).
\({x^3} + C\).
Đạo hàm của hàm số \(y = \cos 5x\) tại \(x = \frac{\pi }{6}\) bằng
\(\frac{{5\sqrt 3 }}{2}\).
\( - \frac{5}{2}\).
\( - \frac{{5\sqrt 3 }}{2}\).
\(\frac{5}{2}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho vectơ \(\overrightarrow u = \overrightarrow i - 3\overrightarrow j + 2\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow u \) là
\[\left( {1;2;3} \right)\].
\[\left( {2;3;1} \right)\].
\[\left( {1; - 3;2} \right)\].
\[\left( {2; - 3;1} \right)\].
Trong không gian \[Oxyz\], cho mặt phẳng \(\left( P \right):2x + 3y + z - 1 = 0\). Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) có tọa độ là
\[\left( {2;3;1} \right)\].
\[\left( {1; - 2;3} \right)\].
\[\left( {1;2;3} \right)\].
\[\left( {1; - 3;2} \right)\].
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ.
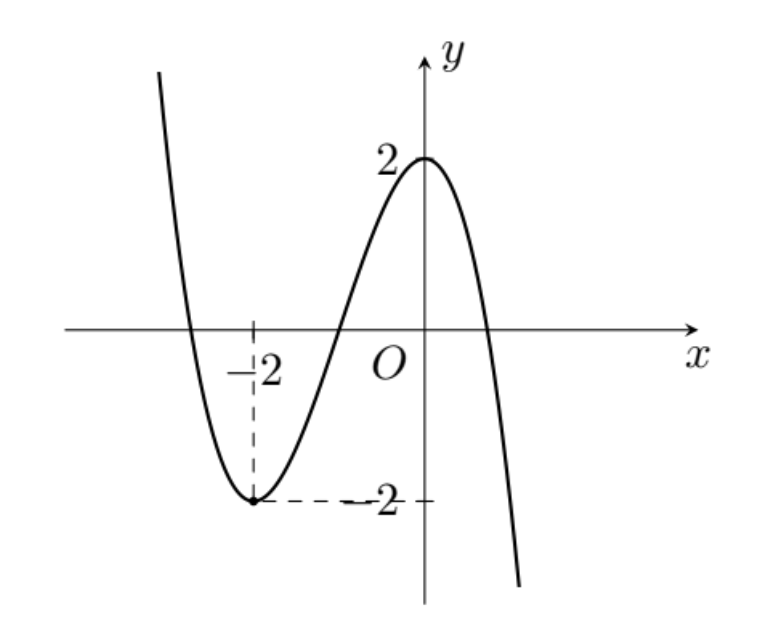
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\[\left( { - \infty ; - 2} \right)\].
\[\left( { - 2;0} \right)\].
\[\left( {0; + \infty } \right)\].
\[\left( { - 1;1} \right)\].
Mỗi ngày bác Lan đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Lan trong \(20\) ngày được thống kê lại ở bảng sau:
Quãng đường (km) | \(\left[ {2,7;3,0} \right)\) | \(\left[ {3,0;3,3} \right)\) | \(\left[ {3,3;3,6} \right)\) | \(\left[ {3,6;3,9} \right)\) | \(\left[ {3,9;4,2} \right)\) |
Số ngày | \(3\) | \(6\) | \(5\) | \(4\) | \(2\) |
Độ lệch chuẩn của mẫu số liệu ghép nhóm này có giá trị gần nhất với giá trị nào dưới đây?
\(0,25\).
\(0,27\).
\(0,42\).
\(0,36\).
Tập nghiệm của phương trình \({\left( {0,2} \right)^x} \le 4\) là
\(\left( { - \infty ;{{\log }_4}0,2} \right]\).
\[\left[ {{{\log }_{0,2}}4; + \infty } \right)\].
\(\left( { - \infty ;{{\log }_{0,2}}4} \right]\).
\[\left[ {{{\log }_4}0,2; + \infty } \right)\].
Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\) có phương trình \[{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 9\]. Toạ độ tâm của mặt cầu đã cho là:
\[\left( {2; - 1;3} \right)\].
\[\left( { - 2;1;3} \right)\].
\[\left( { - 2;1; - 3} \right)\].
\[\left( { - 2; - 1;3} \right)\].
Cho hình lập phương \[ABCD.A'B'C'D'\].
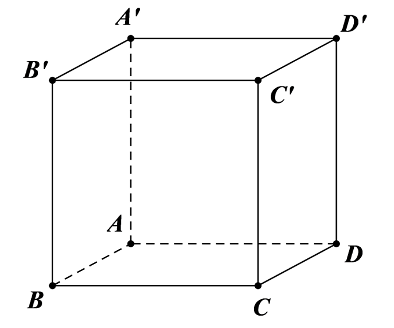
Đường thẳng nào sau đây vuông góc với mặt phẳng \[\left( {CDD'C'} \right)\]?
\[A'B\].
\[BC\].
\[AD'\].
\[AB\].
Cho hàm số\[f\left( x \right)\]có đạo hàm \[f'\left( x \right)\] liên tục trên\[\mathbb{R}\], \[f\left( 1 \right) = 1\] và \[\int\limits_1^4 {f'\left( x \right){\rm{d}}x} = 15\], khi đó giá trị \[f\left( 4 \right)\]bằng:
\[16\].
\[15\].
\[14\].
\[17\].
Cho cấp số cộng \[\left( {{u_n}} \right)\]có \[{u_1} = 5,{\kern 1pt} \;{u_7} = 29\]. Công sai của cấp số cộng đã cho là
\[d = 24\].
\[d = \frac{{29}}{5}\].
\[d = 4\].
\[d = 145\].
Số nghiệm của phương trình \[\cos x{\rm{ = 0}}\] thuộc khoảng \[\left( {0;2\pi } \right)\] là:
\[1\].
\[3\].
\[4\].
\[2\].
a) Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
b) Hàm số có đạo hàm là \[y' = 1 - \frac{9}{{{{\left( {x + 2} \right)}^2}}}\].
c) Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 5} \right)\,\,{\rm{v\`a }}\,\,\left( {1; + \infty } \right)\).
d) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
a) Quãng đường xe mô tô đi được sau 10 phút là \[5\,{\rm{km}}\].
b) Giá trị của \[b\] là \[30\].
c) Thời gian ô tô bắt đầu tăng tốc cho đến khi đạt tốc độ \(60\,\,{\rm{km/h}}\) là 3 giây.
d) Biết quãng đường Sóc Trăng – Cần Thơ dài \(60\,\,{\rm{km}}\), sau khi ô tô gặp mô tô thì ô tô di chuyển thêm \[29\,{\rm{km}}\] thì đến Cần Thơ (làm tròn kết quả đến hàng đơn vị).
a) Xác suất \(P\left( A \right) = 0,01\) và \(P\left( {\overline A } \right) = 0,99\).
b)Xác suất \(P\left( B \right) = 0,0395\).
c) Xác suất có điều kiện \(P\left( {A|B} \right) = 0,7\).
d) Trong số những bài viết bị phần mềm cảnh báo là đạo văn, có nhiều khả năng là bài viết chính chủ hơn là đạo văn.
a) Điểm \(A\) không thuộc đường thẳng \(d\).
b) Mặt phẳng \(\left( P \right)\) đi qua \(A\) và vuông góc \(d\) có phương trình là \(2x + y + 3z + 4 = 0\).
c) Giao điểm của \(d\) và \(\left( P \right)\) là điểm \(K\left( {\frac{2}{7}; - \frac{{33}}{{14}};\frac{{27}}{{14}}} \right)\).
d) Gọi \(\left( Q \right)\) là mặt phẳng chứa \(d\) sao cho khoảng cách từ điểm \(A\) đến \(\left( Q \right)\) là lớn nhất. Khi đó mặt phẳng \(\left( Q \right)\) có phương trình là \(24x + 75y - 41z + 249 = 0\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Trong trung tâm thương mại Lotte thành phố Vĩnh Yên, có một nhà hàng bán buffet hải sản. Khi nhà hàng bán với giá 200 nghìn đồng một suất thì mỗi ngày nhà hàng bán được 100 suất. Nhà hàng dự định có đợt giảm giá bán để kích cầu trong dịp cuối năm. Theo khảo sát từ thị trường thì mỗi lần giảm giá 10 nghìn đồng một suất thì nhà hàng bán thêm được 10 suất, hỏi nhà hàng cần bán với giá mới là bao nhiêu nghìn đồng một suất để doanh thu trong một ngày là lớn nhất?
Trong một đợt diễn tập quốc phòng, hai người ở vị trí khác nhau cùng ngắm bắn một mục tiêu cố định trên không. Người ta gắn một hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục tính theo mét), mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất. Người thứ nhất bắn một viên đạn đi qua hai điểm \(A\left( {5;\,7;\,10} \right)\) và \(B\left( {6;\,9;\,12} \right)\). Người thứ hai bắn một viên đạn đi qua hai điểm \(C\left( {15;\,17;\,5} \right)\) và \(D\) (điểm \(D\) ở độ cao \(26\,{\rm{m}}\) so với mặt đất). Biết rằng sau một thời gian rời khỏi nòng súng, hai viên đạn chạm với nhau tại vị trí cách điểm \(A\) một khoảng \(150\,{\rm{m}}\)(tham khảo hình vẽ).
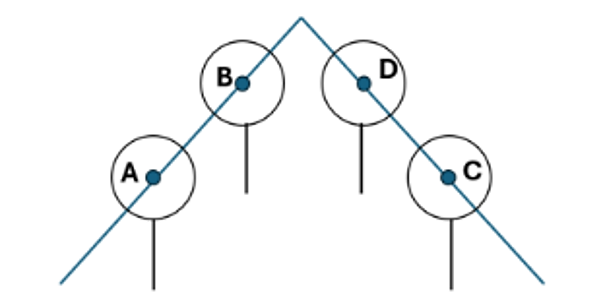
Hỏi \(D\) cách \(C\) một khoảng bao nhiêu mét? (kết quả làm tròn đến hàng phần chục).
Cho một hộp quà hình lập phương có cạnh bằng \(10\,\,{\rm{cm}}\). Trong hộp có một quả cầu pha lê lớn đặc được đặt vừa khít vào hộp sao cho quả cầu tiếp xúc với tất cả các mặt của hộp. Ở 8 góc của hình lập phương, có 8 quả cầu pha lê nhỏ cùng tiếp xúc với các mặt hộp và tiếp xúc với quả cầu lớn. Đổ epoxy resin (một loại keo tổng hợp trong suốt dùng trong thủ công mỹ nghệ) vào đầy hộp để trang trí. Tính thể tích phần keo cần đổ, theo đơn vị lít (làm tròn kết quả đến hàng phần mười).
Tính hết năm \(2022\) diện tích rừng của thành phố \(X\) là \(140600\,{\rm{ha}}\), tỷ lệ che phủ rừng trên địa bàn thành phố đạt \(39,8\% \). Trong năm \(2022\) thành phố \(X\)trồng mới được \(1000\,{\rm{ha}}\). Giả sử diện tích rừng trồng mới của thành phố mỗi năm tiếp theo đều tăng \(6\% \) so với diện tích rừng trồng mới của năm liền trước. Sau ít nhất bao nhiêu năm thành phố có diện tích rừng đạt tỷ lệ che phủ \(45\% \)?
Xác suất bé An được mẹ dẫn theo khi đi mua sắm là \(\frac{2}{5}.\) Khi bé An được đi theo mẹ thì 70% bé sẽ được mua đồ chơi. Khi bé không đi theo mẹ, có thể mẹ vẫn mua đồ chơi cho bé. Xác suất bé được đi theo mẹ biết rằng bé được mẹ mua cho đồ chơi là \(\frac{{14}}{{23}}.\) Khi bé không đi theo mẹ, xác suất bé được mẹ mua cho đồ chơi là bao nhiêu?
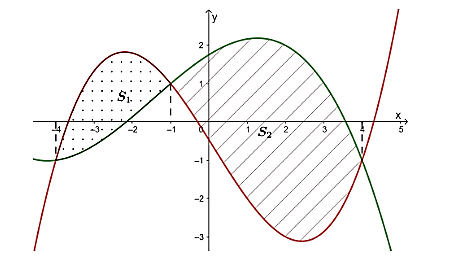
Cho các hàm số
\(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) và \(g\left( x \right) = m{x^3} + n{x^2} + px + q\)\(\left( {a,b,c,d,m,n,p,q \in \mathbb{R}} \right)\).
Biết rằng đồ thị của hai hàm số \(f\left( x \right)\) và \(g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 4;{\rm{ }} - 1;{\rm{ }}4\) và \(f\left( 2 \right) = 2;{\rm{ }}g\left( 2 \right) = - 3\) (tham khảo hình vẽ bên dưới). Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = - 4;{\rm{ }}x = - 1\). Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = - 1;{\rm{ }}x = 4\). Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}\)(làm tròn kết quả đến hàng phần trăm).