Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 46)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Tìm nguyên hàm của hàm số \[f\left( x \right) = \frac{1}{{5x - 12}}\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = \frac{1}{5}\ln \left| {12 - 5x} \right| + C\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = - \frac{1}{5}\ln \left| {5x - 12} \right| + C\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = 5\ln \left| {5x - 12} \right| + C\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = \ln \left| {5x - 12} \right| + C\].
Trong không gian \[Oxyz\], phương trình nào sau đây là phương trình chính tắc của đường thẳng \[d:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3t\\z = - 3 + t\end{array} \right.\]?
\[\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 3}}{{ - 2}}\].
\[\frac{{x - 1}}{1} = \frac{y}{3} = \frac{{z + 3}}{{ - 2}}\].
\[\frac{{x + 1}}{2} = \frac{{y - 3}}{3} = \frac{{z + 3}}{1}\].
\[\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z + 3}}{1}\].
Cho hình hộp \[ABCD.EFGH\] (minh họa hình dưới).

Kết quả của phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là
\[\overrightarrow {FH} \].
\[\overrightarrow {BH} \].
\[\overrightarrow {DB} \].
\[\overrightarrow {AE} \] .
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\left( {a,b,c,d \in \mathbb{R}} \right)\] có đồ thị là đường cong như hình vẽ dưới đây.
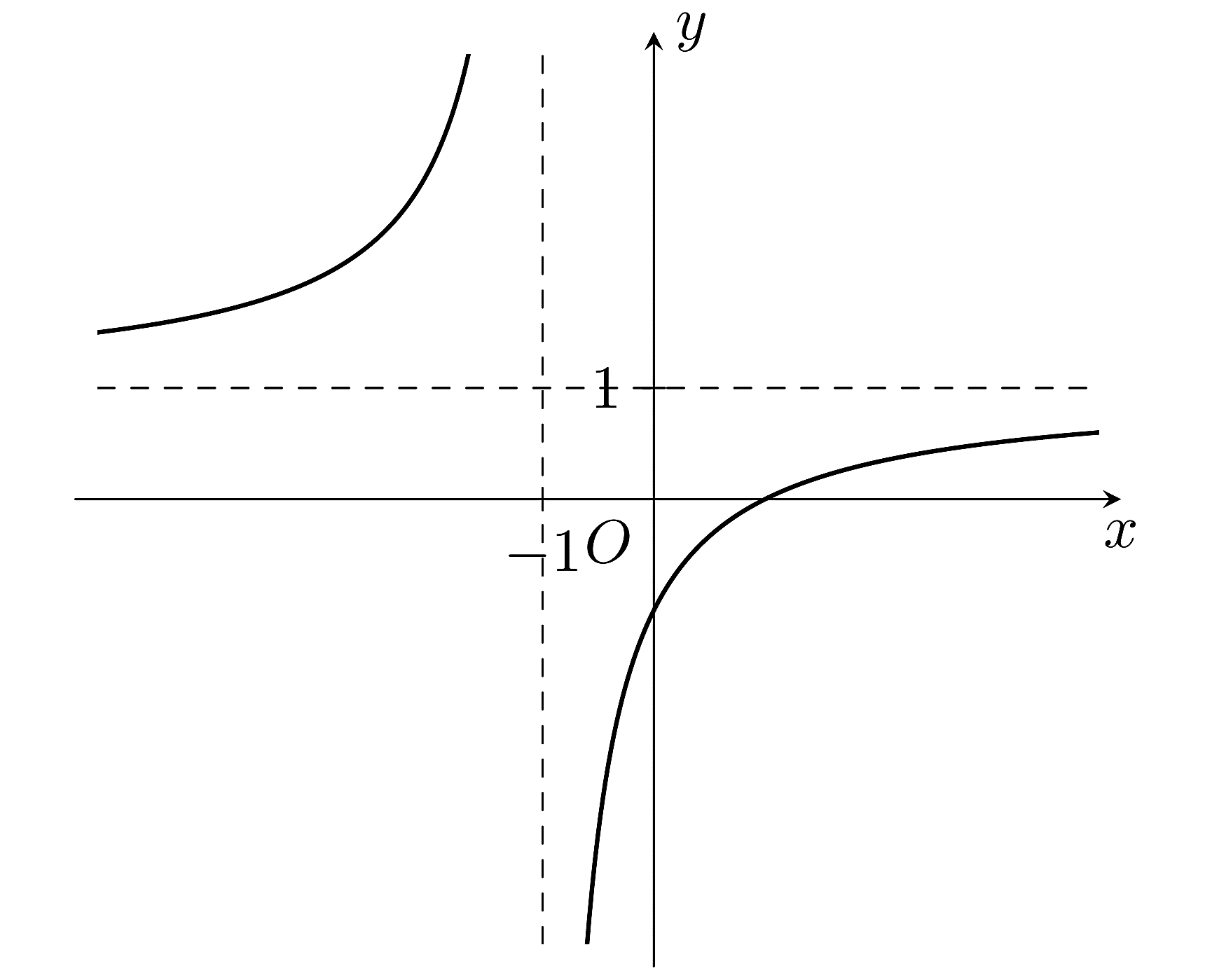
Toạ độ tâm đối xứng của đồ thị hàm số đã cho là:
\[\left( { - 1;1} \right)\].
\[\left( {1;1} \right)\].
\[\left( {1; - 1} \right)\].
\[\left( {0;1} \right)\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới.
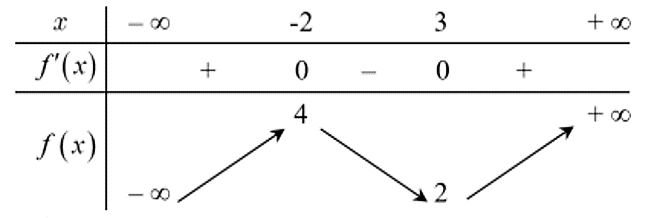
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( { - 1;2} \right)\).
\(\left( { - 8; - 3} \right)\).
\(\left( { - \infty ;4} \right)\).
\(\left( {2; + \infty } \right)\).
Cho hình chóp có diện tích mặt đáy là \(4{a^2}\)và chiều cao bằng \(3a\). Thể tích của khối chóp tương ứng bằng
\(4{a^3}\).
\(12{a^3}\).
\(2{a^3}\).
\(6{a^3}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 3,{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 5\). Gọi \(V\)là thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\)xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
\(V = \int\limits_0^5 {\left( {{x^2} + 3} \right)} \,{\rm{d}}x\).
\(V = \pi \int\limits_0^5 {{{\left( {{x^2} + 3} \right)}^2}} {\rm{d}}x\).
\(V = \int\limits_0^5 {{{\left( {{x^2} + 3} \right)}^2}} {\rm{d}}x\).
\(V = \pi \int\limits_0^5 {\left( {{x^2} + 3} \right)} \,{\rm{d}}x\).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {5; - 4;2} \right)\)và \(B\left( {1;2;4} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với đường thẳng \(AB\) là
\(2x - 3y - z - 20 = 0\).
\(3x - y + 3z - 25 = 0\).
\(3x - y + 3z - 13 = 0\).
\(2x - 3y - z + 8 = 0\).
Tập nghiệm của bất phương trình \(\log x \ge 1\) là:
\(\left[ {10; + \infty } \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( {10; + \infty } \right)\).
\(\left( { - \infty ;10} \right)\).
Khảo sát thời gian tự học ở nhà của học sinh khối 12 ở trường X, ta thu được bảng sau:
Thời gian (phút) | \(\left[ {0;30} \right)\) | \(\left[ {30;60} \right)\) | \(\left[ {60;90} \right)\) | \(\left[ {90;120} \right)\) | \(\left[ {120;150} \right)\) |
Số học sinh tự học | \(75\) | \(125\) | \(250\) | \(82\) | \(18\) |
Phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng đơn vị) là
\(874\).
\(872\).
\(873\).
\(875\).
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
\(y = {\log _{\frac{1}{2}}}x\).
\(y = {3^{ - x}}\).
\(y = {2025^x}\).
\(y = {2^x}\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội \(q = 2\). Giá trị của \({u_3}\) bằng
\(12\).
\(18\).
\(7\).
\(6\).
a) \(f\left( 0 \right) = 0,f\left( \pi \right) = \sqrt 3 \pi \).
b) Đạo hàm của hàm số đã cho là \(f'\left( x \right) = - 2\cos x + \sqrt 3 \).
c) Nghiệm của phương trình \(f'\left( x \right) = 0\) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6}\).
d) Giá trị lớn nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {0;\pi } \right]\) bằng \(1 + \frac{{5\sqrt 3 \pi }}{6}\).
a) Một vectơ chỉ phương của đường thẳng \[AB\] là \(\vec u = \left( {0;5;1} \right)\).
b) Khi người thợ điện di chuyển đến vị trí điểm \[D\] cách mặt đất \[18\,{\rm{m}}\] thì tọa độ điểm \[D\] là \(D\left( {7; - 5;18} \right)\).
c) Phương trình mặt phẳng \(\left( {ABC} \right)\) là \(x = 7\).
d) Khoảng cách từ Puly tại \[A\] đến bàn đạp tại \[C\] là \[1,03\,{\rm{m}}\](kết quả làm tròn đến hàng phần trăm).
a)\(f\left( x \right) = x + \frac{2}{x}\).
b)\(\int {f\left( x \right){\rm{d}}x = \frac{{{x^2}}}{2}} + 2\ln x + C\).
c) Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) thỏa mãn \(F\left( 1 \right) = \frac{3}{2}\). Khi đó \(F\left( 4 \right) = 9 + 4\ln 2\).
d) Nếu \(\int\limits_1^4 {kf\left( x \right){\rm{d}}x = 5} \) thì \(k \in \left( {1;2} \right)\).
a)\[P\left( A \right) = \frac{1}{2}\].
b)\[P\left( {B\mid A} \right) = \frac{3}{8}\].
c) Xác suất để người đó chọn được đồng xu cân bằng biết rằng kết quả ba lần tung đều xuất hiện mặt ngửa là \[0,25\] (kết quả làm tròn đến hàng phần trăm).
d) Biết rằng đồng xu được chọn tung ba lần đều xuất hiện mặt ngửa, xác suất người chơi đó tung lần thứ tư tiếp tục xuất hiện mặt ngửa là \[0,69\] (kết quả làm tròn đến hàng phần trăm).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty đang triển khai chiến dịch quảng cáo sản phẩm mới. Số tiền đầu tư quảng cáo là A (triệu đồng). Theo kết quả nghiên cứu thị trường, số lượng sản phẩm bán ra (đơn vị: sản phẩm) phụ thuộc vào chi phí quảng cáo theo hàm số \[q\left( A \right) = 1000 + \frac{{1013}}{5}\ln \left( {1 + A} \right)\].
Biết rằng, chi phí sản xuất mỗi sản phẩm là 10 triệu đồng và giá bán mỗi sản phẩm là 20 triệu đồng. Giá trị lợi nhuận tối đa mà công ty có thể đạt được là bao nhiêu tỉ đồng (làm tròn kết quả đến hàng phần mười)?
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông cân tại \(C\) và \[AC = 4\]. Biết \[SA\] vuông góc với mặt phẳng đáy và khoảng cách từ \(A\) đến mặt phẳng \[\left( {SBC} \right)\] bằng \(\frac{{12}}{5}\). Thể tích của khối chóp \[S.ABC\] bằng bao nhiêu?
Một bức tường hình chữ nhật \[ABCD\]có kích thước lần lượt là \[6{\rm{ m}}\]và \[4\,\,{\rm{m}}\]được bạn Minh trang trí bằng cách vẽ hai đồ thị hàm số \[f\left( x \right) = {a^x}\]\[\left( {0 < a \ne 1} \right)\] và \[g\left( x \right) = {\log _b}x\]\[\left( {0 < b \ne 1} \right)\]đối xứng nhau qua đường thẳng \[y = x\]. Bức tường được chia làm 3 phần (tham khảo hình vẽ).
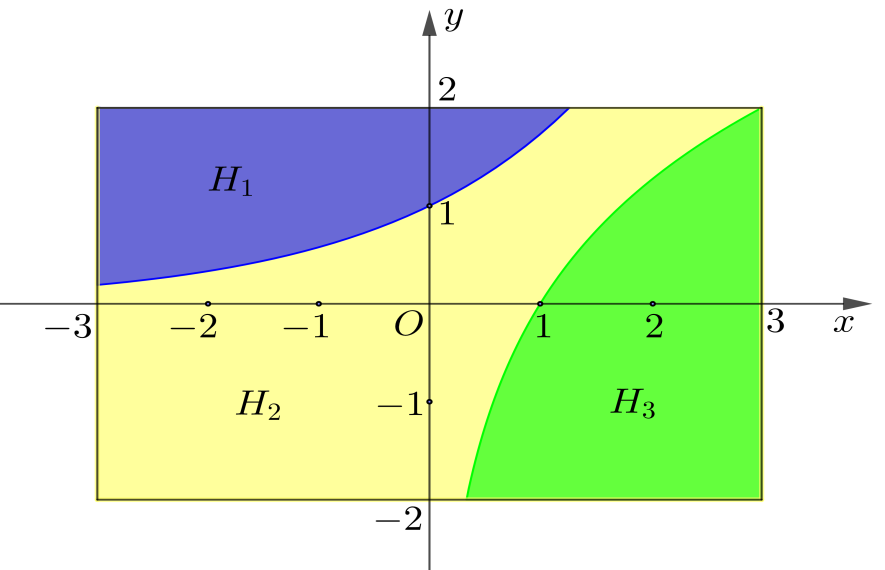
Phần \[{H_1}\]được sơn màu xanh da trời, phần \[{H_2}\]sơn màu vàng và phần \[{H_3}\]được sơn màu xanh lá cây. Bạn Minh cần mua các hộp sơn mà mỗi hộp chỉ sơn được một màu tương ứng với các màu mà bạn Minh định sơn. Biết rằng mỗi hộp sơn chỉ sơn được tối đa \[3{\rm{ }}{{\rm{m}}^{\rm{2}}}\] tường, giá một hộp sơn màu xanh da trời là 120 000 đồng, giá một hộp sơn màu xanh lá cây là 140 000 đồng, giá một hộp sơn màu vàng là 160 000 đồng. Cửa hàng chỉ bán số các hộp sơn là các số nguyên dương. Bạn Minh cần bao nhiêu triệu đồng để sơn bức tường đó?
Tại một khu trung tâm dữ liệu, kỹ sư IT cần kiểm tra kết nối giữa các máy chủ trong hệ thống gồm các trạm \(A,\,B,\,C,\,D,\,E.\) Các tuyến cáp quang nối giữa các trạm được biểu diễn trong sơ đồ sau, với con số ghi trên mỗi tuyến là chiều dài dây cáp (đơn vị: km).
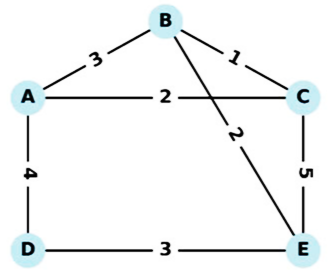
Kỹ sư cần thực hiện một hành trình bắt đầu từ một trạm bất kì, đi qua tất cả các tuyến cáp ít nhất một lần, và kết thúc tại đúng trạm khởi hành, nhằm đảm bảo toàn bộ hệ thống được kiểm tra. Tổng chiều dài đường đi ngắn nhất mà kỹ sư cần di chuyển là bao nhiêu kilômét?
Trong một trung tâm nghiên cứu robot bay, người ta bố trí một thiết bị định vị tại điểm cố định \(A\left( {1\,;0\,;2} \right)\) trong không gian ba chiều với hệ tọa độ \(Oxyz\) (các đơn vị tọa độ được tính bằng mét). Thiết bị này giao tiếp đồng thời với hai cảm biến: Cảm biến thứ nhất di chuyển dọc theo đường thẳng \(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 4}}{{ - 1}}\), cảm biến thứ hai được gắn trên mặt phẳng \(\left( \alpha \right):2x - y + z + 1 = 0\). Giữa hai cảm biến được kết nối bằng một đường truyền \(BC,\) trong đó \(B\) nằm trên đường thẳng \(\Delta ,C\) nằm trên mặt phẳng \(\left( \alpha \right)\) và thiết bị định vị tại \(A\) là trung điểm của đoạn \(BC.\) Biết rằng đường thẳng \(BC\) có một vectơ chỉ phương \(\vec u = \left( { - 2\,;a\,;b} \right)\),hãy tính giá trị \(a + 2b.\)
Một người tham gia trò chơi với \[3\]hộp quà đặc biệt: Hộp màu vàng có \[2\] điện thoại iPhone và \[3\] tai nghe, hộp màu bạc có \[4\] điện thoại iPhone và \[1\] tai nghe, hộp màu đồng có \[3\] điện iPhone và \[2\] tai nghe. Luật chơi được thực hiện qua hai bước sau:
Bước 1. Người chơi chọn ngẫu nhiên \[1\] hộp.
Bước 2. Từ hộp đã chọn, người chơi lấy ngẫu nhiên \[1\] món quà:
- Nếu quà là điện thoại iPhone, người chơi được giữ nó và lấy thêm \[1\] quà nữa từ cùng hộp.
- Nếu quà là tai nghe, trò chơi kết thúc.
Biết rằng người chơi lấy được \[2\] điện thoại iPhone, tính xác suất để người đó lấy từ hộp màu bạc (làm tròn kết quả đến hàng phần mười).