Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 47)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây.
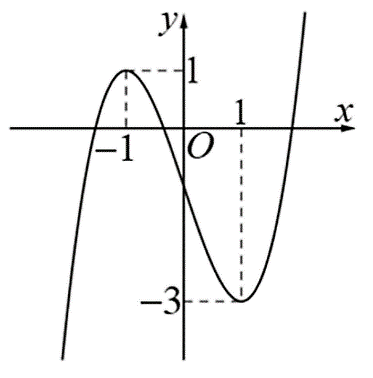
Điểm cực tiểu của đồ thị hàm số trên là
\(x = 1\).
\(N\left( { - 1;1} \right)\).
\(M\left( {1; - 3} \right)\).
\(x = - 1\).
Trong không gian \(Oxyz,\) cho tam giác \(ABC\) có \(A\left( {2; - 3;1} \right),B\left( {1;3; - 4} \right)\) và \(C\left( {3; - 3;6} \right).\) Trọng tâm của tam giác \(ABC\) có tọa độ là
\(\left( {2; - 1;1} \right)\).
\(\left( { - 6;3; - 3} \right)\).
\(\left( {6; - 3;3} \right)\).
\(\left( { - 2;1; - 1} \right)\).
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{{x - 3}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{2}.\)Điểm nào sau đây không thuộc đường thẳng \(d?\)
\(P\left( {5; - 3;1} \right)\).
\(N\left( {2; - 1; - 3} \right)\).
\(Q\left( { - 1;0; - 5} \right)\).
\(M\left( { - 3;1; - 7} \right)\).
Giải bất phương trình \({\log _2}\left( {3x - 1} \right) < 3\), ta được tập nghiệm là \(\left( {a;b} \right)\). Hãy tính giá trị của biểu thức \(S = a + b\).
\(S = 3\).
\(S = \frac{{10}}{3}\).
\(S = \frac{5}{3}\).
\(S = \frac{1}{3}\).
Họ tất cả nguyên hàm của hàm số \(f\left( x \right) = 4x + 3\) là
\(2{x^2} + C\).
\(2{x^2} + 3x + C\).
\(4{x^2} + C\).
\(4{x^2} + 3x + C\).
Một cửa hàng quần áo khảo sát một số khách hàng xem họ dự định mua quần áo cho trẻ em với mức giá nào (đơn vị: nghìn đồng). Kết quả khảo sát được ghi lại ở bảng sau:
Mức giá | \(\left[ {60;90} \right)\) | \(\left[ {90;120} \right)\) | \(\left[ {120;150} \right)\) | \(\left[ {150;180} \right)\) | \(\left[ {180;210} \right)\) |
Số khách hàng | 20 | 75 | 48 | 25 | 12 |
Nửa khoảng \(\left[ {a;b} \right),{\rm{ }}\left( {a,b \in \mathbb{R}} \right)\) chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên. Tính tổng \(S = a + b\) được kết quả là
\(210\).
\(150\).
\(45\).
\(30\).
Có bao nhiêu nghiệm nguyên trong đoạn \(\left[ { - 5;5} \right]\) của bất phương trình \({\left( {\frac{1}{2}} \right)^{x + 2}} \le 2\).
\(3\).
\(8\).
\(10\).
\(9\).
Trong không gian \[Oxyz\], cho hai vectơ \[\overrightarrow u = \overrightarrow i + 3\overrightarrow j - 2\overrightarrow k \] và \[\overrightarrow v = \left( {2; - 1;1} \right)\]. Tích vô hướng \[\overrightarrow u \cdot \overrightarrow v \] bằng
\[ - 12\].
\[5\sqrt 2 \].
\[ - 3\].
\[2\sqrt {21} \].
Cho hàm số \(y = f\left( x \right)\) xác định với mọi \(x \ne 2\) có bảng biến thiên như hình vẽ.
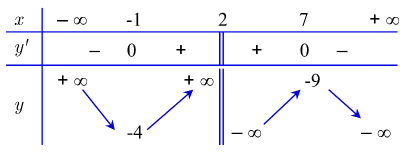
Hàm số đồng biến trên khoảng nào trong các khoảng sau?
\(\left( { - 1;7} \right)\).
\(\left( {2;7} \right)\).
\(\left( { - 1;7} \right)\backslash \left\{ 2 \right\}\).
\(\left( {2; + \infty } \right)\).
Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{{x - 4}}{{ - 3}} = \frac{{y + 1}}{{ - 2}} = \frac{{z - 3}}{{ - 5}}\). Phương trình tham số của đường thẳng \(d\) là
\(\left\{ \begin{array}{l}x = 4 - 3t\\y = - 1 - 2t\\z = 3 - 5t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = 3 + 4t\\y = 2 - t\\z = 5 + 3t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = - 3 + 4t\\y = - 2 - t\\z = - 5 + 3t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = 4 + 3t\\y = 1 + 2t\\z = 3 + 5t\end{array} \right.\).
Một trường học tổ chức trải nghiệm cho học sinh bằng cách tổ chức các trò chơi, trong đó có trò chơi sử dụng đồng xu để xếp thành một kim tự tháp. Yêu cầu mỗi nhóm học sinh sử dụng \(253\) đồng tiền xu để xếp một mô hình kim tự tháp. Biết rằng tầng dưới cùng có \(58\) đồng xu và cứ lên thêm một tầng thì số đồng xu giảm đi \(7\) đồng. Tập hợp số xu ở mỗi tầng tạo thành
một cấp số nhân với số hạng đầu và công bội lần lượt là \({u_1} = 58;q = 7\).
một cấp số cộng với số hạng đầu và công sai lần lượt là \({u_1} = 58;d = - 7\).
một cấp số cộng với số hạng đầu và công sai lần lượt là \({u_1} = 58;d = 7\).
một cấp số nhân với số hạng đầu và công bội lần lượt là \({u_1} = 58;q = - 7\).
Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = 3{x^2}\), \(y = - 2\), \(x = 0\) và \(x = 1\) được tính bởi công thức nào sau đây?
\(S = \int\limits_0^1 {\left( {3{x^2} + 2} \right){\rm{d}}x} \).
\(S = \int\limits_0^1 {\left( {3{x^2} - 2} \right){\rm{d}}x} \).
\(S = \pi \int\limits_0^1 {{{\left( {3{x^2} + 2} \right)}^2}{\rm{d}}x} \).
\(S = \pi \int\limits_0^1 {\left( {3{x^2} + 2} \right){\rm{d}}x} \).
a) \(f\left( e \right) = 3\).
b) Hàm số có tập xác định là \(\left[ {0;4e} \right]\).
c) Phương trình \(f'\left( x \right) = 0\) có một nghiệm \(x = 2e\).
d) Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {1;3e} \right]\) có dạng \(a\ln 2 + b\) thì \(a + b = 4\).
a) Chu vi của chiếc đèn là \[36\pi \] (cm).
b) \[\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = 24{\rm{ N}}\].
c) Khi độ dài của ba sợi dây càng tăng (dài hơn \(18{\rm{ }}\left( {{\rm{inch}}} \right)\)) thì độ lớn các lực căng \(F\) giảm nhưng không vượt quá \[9\,{\rm{N}}\].
d) Chiều dài tối thiểu của mỗi sợi dây để lực căng tối đa \[24\,{\rm{N}}\]là \[27\sqrt 2 \left( {{\rm{inch}}} \right)\].
a) Tọa độ các điểm \(E,F\) là \(E\left( { - 2\sqrt 2 ;2\sqrt 2 } \right),F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
b) Biết \(y = f\left( x \right) = a{x^3} + bx\). Khi đó \(a + b = - 15\).
c) Diện tích phần trồng hoa là \(S = 16 + 8\pi \,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
d) Biết chi phí trồng hoa \(1\,\,{{\rm{m}}^{\rm{2}}}\) là \(180\) nghìn đồng, trồng cỏ \(1\,\,{{\rm{m}}^{\rm{2}}}\) là \(100\) nghìn đồng. Chi phí để hoàn thành công trình trên là \(8117\) nghìn đồng (làm tròn kết quả đến hàng nghìn).
a)\({P_1} = 0,15\).
b)\({P_2} = 0,18\).
c)Nếu xạ thủ đó bắn ba phát thì xác suất đạt \(29\) điểm là \(0,0045\).
d)Nếu xạ thủ đó bắn ba phát thì xác suất đạt ít nhất \(28\) điểm là \(0,05175\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Chi phí về nhiên liệu của một con tàu được chia làm hai phần. Phần chi phí thứ nhất không phụ thuộc vào tốc độ tàu và bằng 480 nghìn đồng mỗi giờ. Chi phí phần thứ hai trên 1 km đường tỉ lệ thuận với lập phương của tốc độ tàu, khi tốc độ bằng \(20\)km/h thì chi phí phần thứ hai bằng 100 nghìn đồng mỗi giờ. Giả sử con tàu đó luôn giữ nguyên tốc độ di chuyển, để tổng chi phí nhiên liệu trên 1 km đường là nhỏ nhất thì tốc độ của con tàu đó bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phầnchục).
Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp đôi thời gian để làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc không quá 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Số tiền lãi lớn nhất mà phân xưởng thu được trong một ngày là bao nhiêu nghìn đồng?
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(3\) và cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Biết góc nhị diện \(\left[ {B,SC,D} \right]\) bằng \(120^\circ \). Tính thể tích khối chóp \(S.ABCD\) bằng bao nhiêu?
Một ly thủy tinh có hình dạng phần chứa nước là một hình parabol tròn xoay. Hình dạng này được tạo ra bằng cách quay một phần của đường parabol quanh trục đối xứng của nó. Biết phần chứa nước của ly có chiều cao tính từ đáy ly lên đến miệng ly là \[10{\rm{ cm}},\] đường kính miệng ly là \[8{\rm{ cm}}\] (chỉ tính phần chứa nước, không tính phần thủy tinh).
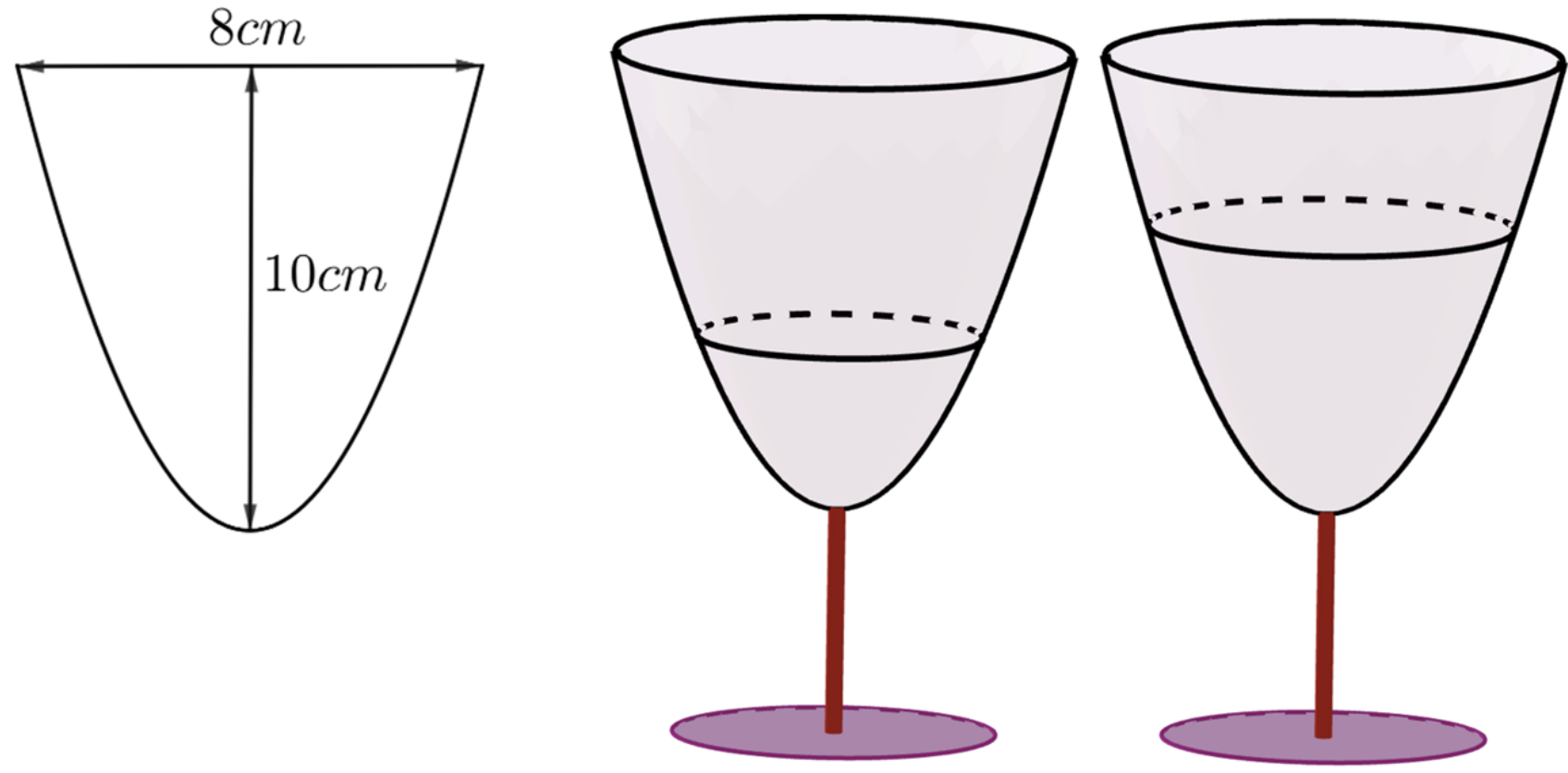
Ban đầu, người ta đổ vào ly một lượng nước có thể tích bằng \(\frac{1}{4}\) thể tích của ly khi nó chứa đầy nước. Sau đó, người ta đổ thêm vào ly một lượng nước có thể tích bằng với lượng nước đã đổ ban đầu. Hỏi sau khi đổ thêm, chiều cao của mực nước trong ly đã tăng thêm bao nhiêu centimét so với lúc ban đầu (làm tròn kết quả đến hàng phần trăm)?
Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí \(A\) cao \(15{\rm{\;m}}\) của tháp 1 này sang vị trí \(B\) cao \(10{\rm{\;m}}\) của tháp 2 trong khung cảnh tuyệt đẹp xung quanh.

Với hệ trục toạ độ \(Oxyz\)cho trước (đơn vị: mét), toạ độ của \(A\) và \(B\) lần lượt là \(A\left( {3;2,5;15} \right)\) và \(B\left( {21;27,5;10} \right)\). Khi du khách khi ở độ cao 12 mét thì tọa độ của du khách lúc đó là \(M\left( {a;b;c} \right)\). Tính giá trị biểu thức \(T = a + b + c\).
Có hai hộp đựng bi. Hộp thứ nhất chứa 7 viên bi màu trắng, 5 viên bi màu đỏ, hộp thứ hai chứa 4 viên bi màu trắng, 6 viên bi màu đỏ. Lấy ngẫu nhiên 2 viên bi từ hộp thứ nhất bỏ sang hộp thứ hai, sau đó lấy ngẫu nhiên 3 viên bi từ hộp thứ hai. Tính xác suất lấy được cả 2 viên bi thuộc hộp thứ nhất bỏ sang hộp thứ hai, biết rằng 3 viên bi đó màu trắng (kết quả làm tròn đến hàng phần mười).