12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
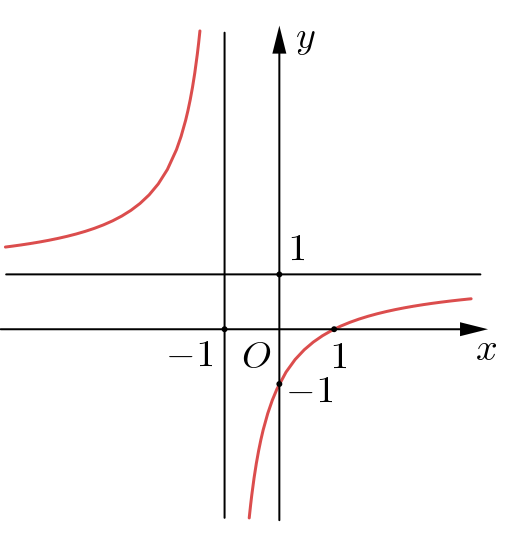
Biểu thức \[f\left( x \right)\] là biểu thức nào sau đây?
\[x + \frac{1}{x}\].
\[ - {x^3} + 3x - 1\].
\[{x^3} - 1\].
\[\frac{{x - 1}}{{x + 1}}\].
Cho hàm số \[f\left( x \right)\] liên tục trên \[\left[ { - 1;5} \right]\] và có đồ thị trên đoạn \[\left[ { - 1;5} \right]\] như hình vẽ dưới.
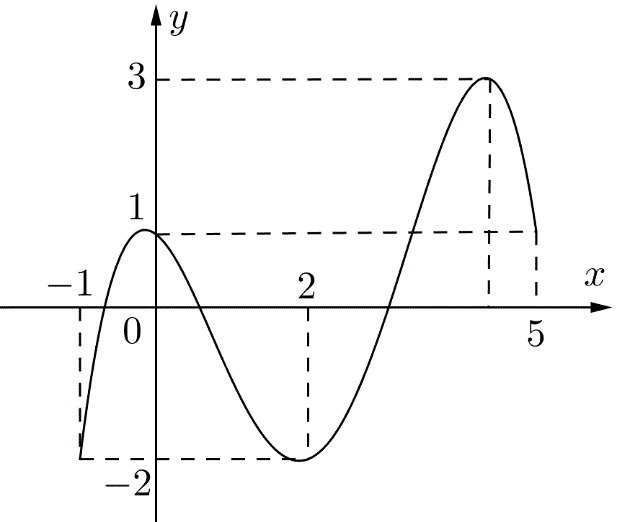
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[f\left( x \right)\] trên đoạn \[\left[ { - 1;5} \right]\]bằng
\[4\].
\[1\].
\[2\].
\[ - 1\].
Trong không gian \[Oxyz\], đường thẳng đi qua điểm \[A\left( {1;1;1} \right)\] và vuông góc với mặt phẳng tọa độ \[\left( {Oxy} \right)\]có phương trình tham số là
\[\left\{ \begin{array}{l}x = 1\\y = 1\\z = 1 + t\end{array} \right.\].
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1 + t\\z = 1\end{array} \right.\].
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1\\z = 1\end{array} \right.\].
\[\left\{ \begin{array}{l}x = 1\\y = 1 + t\\z = 1\end{array} \right.\].
Đường thẳng \[2y + 1 = 0\] là tiệm cận ngang của đồ thị hàm số nào sau đây?
\[y = \frac{{3 - {x^2}}}{{2{x^2} - 3x + 1}}\].
\[y = \frac{{{x^2} + x + 1}}{{1 - 2x}}\].
\[y = \frac{{x + 1}}{{2x + 1}}\].
\[y = \frac{{2x + 1}}{{1 - x}}\].
Cho hai biến cố \(A\) và \(B\), với \(P\left( B \right) = 0,8\);\(P\left( {A|B} \right) = 0,7\);\(P\left( {A|\overline B } \right) = 0,45\). Tính \(P\left( {B|A} \right)\).
\(0,65\).
\(0,25\).
\(0,5\).
\(\frac{{56}}{{65}}\).
Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình.
|
Thời gian (phút) |
\[\left[ {10;15} \right)\] |
\[\left[ {15;20} \right)\] |
\[\left[ {20;25} \right)\] |
\[\left[ {25;30} \right)\] |
\[\left[ {30;35} \right)\] |
|
Số ngày tập của Hưng |
\[2\] |
\[14\] |
\[8\] |
\[3\] |
\[3\] |
|
Số ngày tập của Bình |
\[12\] |
\[8\] |
\[7\] |
\[3\] |
\[0\] |
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập của Hưng và Bình lần lượt là
\[20\]phút và \[25\]phút.
\[25\]phút và \[20\]phút.
\[20\]phút và \[20\]phút.
\[25\]phút và \[25\]phút.
Trong không gian \(Oxyz\), phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;2;1} \right)\) và đi qua điểm \(A\left( {0;4; - 1} \right)\)là
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 3\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\).
Trong không gian \(Oxyz\), một vectơ pháp tuyến của mặt phẳng \(\frac{x}{{ - 2}} + \frac{y}{{ - 1}} + \frac{z}{3} = 1\) là
\(\overrightarrow n = \left( { - 3; - 6; - 2} \right)\).
\(\overrightarrow n = \left( { - 2; - 1;3} \right)\).
\(\overrightarrow n = \left( {2; - 1;3} \right)\).
\(\overrightarrow n = \left( {3;6; - 2} \right)\).
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục \[Ox\]tại \[x = 1\] và \[x = 2\]. Một mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\]\[\left( {1 \le x \le 2} \right)\] cắt vật thể đó có diện tích \[S\left( x \right) = 2026x\]. Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
\(1518\pi \).
\(3039\).
\(3039\pi \).
\(3036\).
Tìm tất cả nguyên hàm \[F\left( x \right)\] của hàm số \[f\left( x \right) = x - \frac{1}{x}\].
\(\frac{1}{2}{x^2} - \ln \left| x \right|\).
\(\frac{1}{2}{x^2} - \ln \left| x \right| + C\).
\(\frac{1}{2}{x^2} - \ln x + C\).
\(1 - \ln \left| x \right| + C\).
Trong không gian với hệ tọa độ \[Oxyz\], cho mặt phẳng \[\left( P \right):6x + 8y + 10z - 1 = 0\] và đường thẳng \[d:\frac{{x - 2}}{3} = \frac{{y + 1}}{4} = \frac{{z - 5}}{5}\]. Góc giữa đường thẳng \[d\] và mặt phẳng \[\left( P \right)\] là
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} = 6\) và công bội \(q = - \frac{1}{2}\). Tính \({u_5}\).
\(\frac{3}{8}\).
\( - 3\).
\( - \frac{3}{8}\).
\( - \frac{4}{3}\).
