12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + 2\) là:
\(2x + C\).
\(3{x^2} + 2x + C\).
\({x^3} + 2x + C\).
\({x^3} + C\).
Đạo hàm của hàm số \(y = \cos 5x\) tại \(x = \frac{\pi }{6}\) bằng
\(\frac{{5\sqrt 3 }}{2}\).
\( - \frac{5}{2}\).
\( - \frac{{5\sqrt 3 }}{2}\).
\(\frac{5}{2}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho vectơ \(\overrightarrow u = \overrightarrow i - 3\overrightarrow j + 2\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow u \) là
\[\left( {1;2;3} \right)\].
\[\left( {2;3;1} \right)\].
\[\left( {1; - 3;2} \right)\].
\[\left( {2; - 3;1} \right)\].
Trong không gian \[Oxyz\], cho mặt phẳng \(\left( P \right):2x + 3y + z - 1 = 0\). Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) có tọa độ là
\[\left( {2;3;1} \right)\].
\[\left( {1; - 2;3} \right)\].
\[\left( {1;2;3} \right)\].
\[\left( {1; - 3;2} \right)\].
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ.
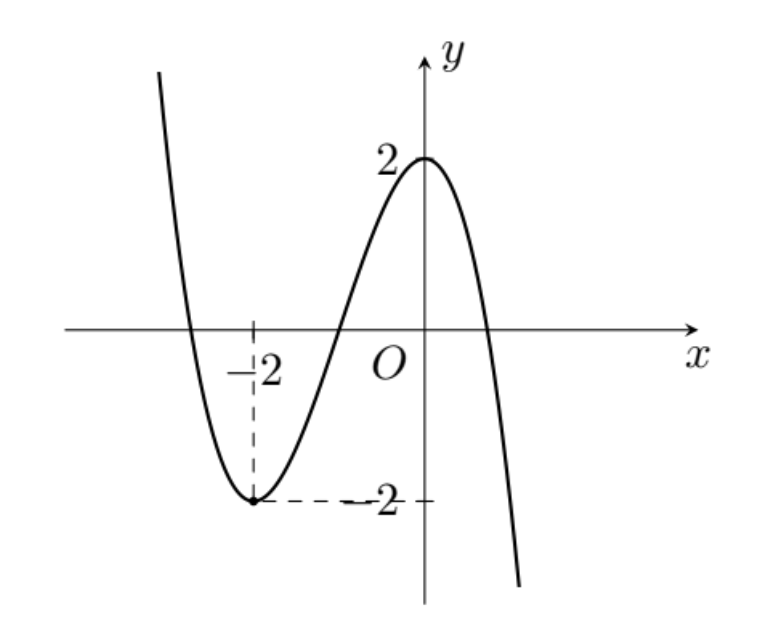
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\[\left( { - \infty ; - 2} \right)\].
\[\left( { - 2;0} \right)\].
\[\left( {0; + \infty } \right)\].
\[\left( { - 1;1} \right)\].
Mỗi ngày bác Lan đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Lan trong \(20\) ngày được thống kê lại ở bảng sau:
|
Quãng đường (km) |
\(\left[ {2,7;3,0} \right)\) |
\(\left[ {3,0;3,3} \right)\) |
\(\left[ {3,3;3,6} \right)\) |
\(\left[ {3,6;3,9} \right)\) |
\(\left[ {3,9;4,2} \right)\) |
|
Số ngày |
\(3\) |
\(6\) |
\(5\) |
\(4\) |
\(2\) |
Độ lệch chuẩn của mẫu số liệu ghép nhóm này có giá trị gần nhất với giá trị nào dưới đây?
\(0,25\).
\(0,27\).
\(0,42\).
\(0,36\).
Tập nghiệm của phương trình \({\left( {0,2} \right)^x} \le 4\) là
\(\left( { - \infty ;{{\log }_4}0,2} \right]\).
\[\left[ {{{\log }_{0,2}}4; + \infty } \right)\].
\(\left( { - \infty ;{{\log }_{0,2}}4} \right]\).
\[\left[ {{{\log }_4}0,2; + \infty } \right)\].
Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\) có phương trình \[{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 9\]. Toạ độ tâm của mặt cầu đã cho là:
\[\left( {2; - 1;3} \right)\].
\[\left( { - 2;1;3} \right)\].
\[\left( { - 2;1; - 3} \right)\].
\[\left( { - 2; - 1;3} \right)\].
Cho hình lập phương \[ABCD.A'B'C'D'\].
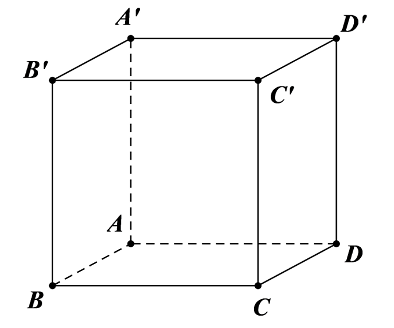
Đường thẳng nào sau đây vuông góc với mặt phẳng \[\left( {CDD'C'} \right)\]?
\[A'B\].
\[BC\].
\[AD'\].
\[AB\].
Cho hàm số\[f\left( x \right)\]có đạo hàm \[f'\left( x \right)\] liên tục trên\[\mathbb{R}\], \[f\left( 1 \right) = 1\] và \[\int\limits_1^4 {f'\left( x \right){\rm{d}}x} = 15\], khi đó giá trị \[f\left( 4 \right)\]bằng:
\[16\].
\[15\].
\[14\].
\[17\].
Cho cấp số cộng \[\left( {{u_n}} \right)\]có \[{u_1} = 5,{\kern 1pt} \;{u_7} = 29\]. Công sai của cấp số cộng đã cho là
\[d = 24\].
\[d = \frac{{29}}{5}\].
\[d = 4\].
\[d = 145\].
Số nghiệm của phương trình \[\cos x{\rm{ = 0}}\] thuộc khoảng \[\left( {0;2\pi } \right)\] là:
\[1\].
\[3\].
\[4\].
\[2\].
