12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây.
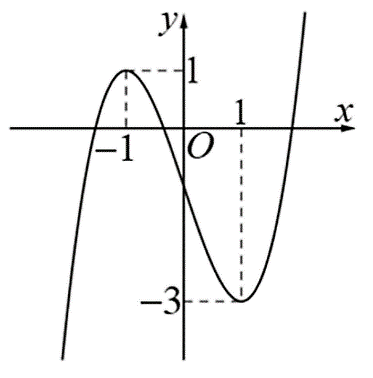
Điểm cực tiểu của đồ thị hàm số trên là
\(x = 1\).
\(N\left( { - 1;1} \right)\).
\(M\left( {1; - 3} \right)\).
\(x = - 1\).
Trong không gian \(Oxyz,\) cho tam giác \(ABC\) có \(A\left( {2; - 3;1} \right),B\left( {1;3; - 4} \right)\) và \(C\left( {3; - 3;6} \right).\) Trọng tâm của tam giác \(ABC\) có tọa độ là
\(\left( {2; - 1;1} \right)\).
\(\left( { - 6;3; - 3} \right)\).
\(\left( {6; - 3;3} \right)\).
\(\left( { - 2;1; - 1} \right)\).
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{{x - 3}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{2}.\)Điểm nào sau đây không thuộc đường thẳng \(d?\)
\(P\left( {5; - 3;1} \right)\).
\(N\left( {2; - 1; - 3} \right)\).
\(Q\left( { - 1;0; - 5} \right)\).
\(M\left( { - 3;1; - 7} \right)\).
Giải bất phương trình \({\log _2}\left( {3x - 1} \right) < 3\), ta được tập nghiệm là \(\left( {a;b} \right)\). Hãy tính giá trị của biểu thức \(S = a + b\).
\(S = 3\).
\(S = \frac{{10}}{3}\).
\(S = \frac{5}{3}\).
\(S = \frac{1}{3}\).
Họ tất cả nguyên hàm của hàm số \(f\left( x \right) = 4x + 3\) là
\(2{x^2} + C\).
\(2{x^2} + 3x + C\).
\(4{x^2} + C\).
\(4{x^2} + 3x + C\).
Một cửa hàng quần áo khảo sát một số khách hàng xem họ dự định mua quần áo cho trẻ em với mức giá nào (đơn vị: nghìn đồng). Kết quả khảo sát được ghi lại ở bảng sau:
|
Mức giá |
\(\left[ {60;90} \right)\) |
\(\left[ {90;120} \right)\) |
\(\left[ {120;150} \right)\) |
\(\left[ {150;180} \right)\) |
\(\left[ {180;210} \right)\) |
|
Số khách hàng |
20 |
75 |
48 |
25 |
12 |
Nửa khoảng \(\left[ {a;b} \right),{\rm{ }}\left( {a,b \in \mathbb{R}} \right)\) chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên. Tính tổng \(S = a + b\) được kết quả là
\(210\).
\(150\).
\(45\).
\(30\).
Có bao nhiêu nghiệm nguyên trong đoạn \(\left[ { - 5;5} \right]\) của bất phương trình \({\left( {\frac{1}{2}} \right)^{x + 2}} \le 2\).
\(3\).
\(8\).
\(10\).
\(9\).
Trong không gian \[Oxyz\], cho hai vectơ \[\overrightarrow u = \overrightarrow i + 3\overrightarrow j - 2\overrightarrow k \] và \[\overrightarrow v = \left( {2; - 1;1} \right)\]. Tích vô hướng \[\overrightarrow u \cdot \overrightarrow v \] bằng
\[ - 12\].
\[5\sqrt 2 \].
\[ - 3\].
\[2\sqrt {21} \].
Cho hàm số \(y = f\left( x \right)\) xác định với mọi \(x \ne 2\) có bảng biến thiên như hình vẽ.
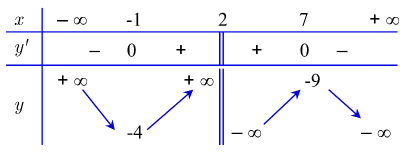
Hàm số đồng biến trên khoảng nào trong các khoảng sau?
\(\left( { - 1;7} \right)\).
\(\left( {2;7} \right)\).
\(\left( { - 1;7} \right)\backslash \left\{ 2 \right\}\).
\(\left( {2; + \infty } \right)\).
Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{{x - 4}}{{ - 3}} = \frac{{y + 1}}{{ - 2}} = \frac{{z - 3}}{{ - 5}}\). Phương trình tham số của đường thẳng \(d\) là
\(\left\{ \begin{array}{l}x = 4 - 3t\\y = - 1 - 2t\\z = 3 - 5t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = 3 + 4t\\y = 2 - t\\z = 5 + 3t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = - 3 + 4t\\y = - 2 - t\\z = - 5 + 3t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = 4 + 3t\\y = 1 + 2t\\z = 3 + 5t\end{array} \right.\).
Một trường học tổ chức trải nghiệm cho học sinh bằng cách tổ chức các trò chơi, trong đó có trò chơi sử dụng đồng xu để xếp thành một kim tự tháp. Yêu cầu mỗi nhóm học sinh sử dụng \(253\) đồng tiền xu để xếp một mô hình kim tự tháp. Biết rằng tầng dưới cùng có \(58\) đồng xu và cứ lên thêm một tầng thì số đồng xu giảm đi \(7\) đồng. Tập hợp số xu ở mỗi tầng tạo thành
một cấp số nhân với số hạng đầu và công bội lần lượt là \({u_1} = 58;q = 7\).
một cấp số cộng với số hạng đầu và công sai lần lượt là \({u_1} = 58;d = - 7\).
một cấp số cộng với số hạng đầu và công sai lần lượt là \({u_1} = 58;d = 7\).
một cấp số nhân với số hạng đầu và công bội lần lượt là \({u_1} = 58;q = - 7\).
Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = 3{x^2}\), \(y = - 2\), \(x = 0\) và \(x = 1\) được tính bởi công thức nào sau đây?
\(S = \int\limits_0^1 {\left( {3{x^2} + 2} \right){\rm{d}}x} \).
\(S = \int\limits_0^1 {\left( {3{x^2} - 2} \right){\rm{d}}x} \).
\(S = \pi \int\limits_0^1 {{{\left( {3{x^2} + 2} \right)}^2}{\rm{d}}x} \).
\(S = \pi \int\limits_0^1 {\left( {3{x^2} + 2} \right){\rm{d}}x} \).
