12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Tìm nguyên hàm của hàm số \[f\left( x \right) = \frac{1}{{5x - 12}}\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = \frac{1}{5}\ln \left| {12 - 5x} \right| + C\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = - \frac{1}{5}\ln \left| {5x - 12} \right| + C\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = 5\ln \left| {5x - 12} \right| + C\].
\[\int {\frac{{{\rm{d}}x}}{{5x - 12}}} = \ln \left| {5x - 12} \right| + C\].
Trong không gian \[Oxyz\], phương trình nào sau đây là phương trình chính tắc của đường thẳng \[d:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3t\\z = - 3 + t\end{array} \right.\]?
\[\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 3}}{{ - 2}}\].
\[\frac{{x - 1}}{1} = \frac{y}{3} = \frac{{z + 3}}{{ - 2}}\].
\[\frac{{x + 1}}{2} = \frac{{y - 3}}{3} = \frac{{z + 3}}{1}\].
\[\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z + 3}}{1}\].
Cho hình hộp \[ABCD.EFGH\] (minh họa hình dưới).

Kết quả của phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là
\[\overrightarrow {FH} \].
\[\overrightarrow {BH} \].
\[\overrightarrow {DB} \].
\[\overrightarrow {AE} \] .
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\left( {a,b,c,d \in \mathbb{R}} \right)\] có đồ thị là đường cong như hình vẽ dưới đây.
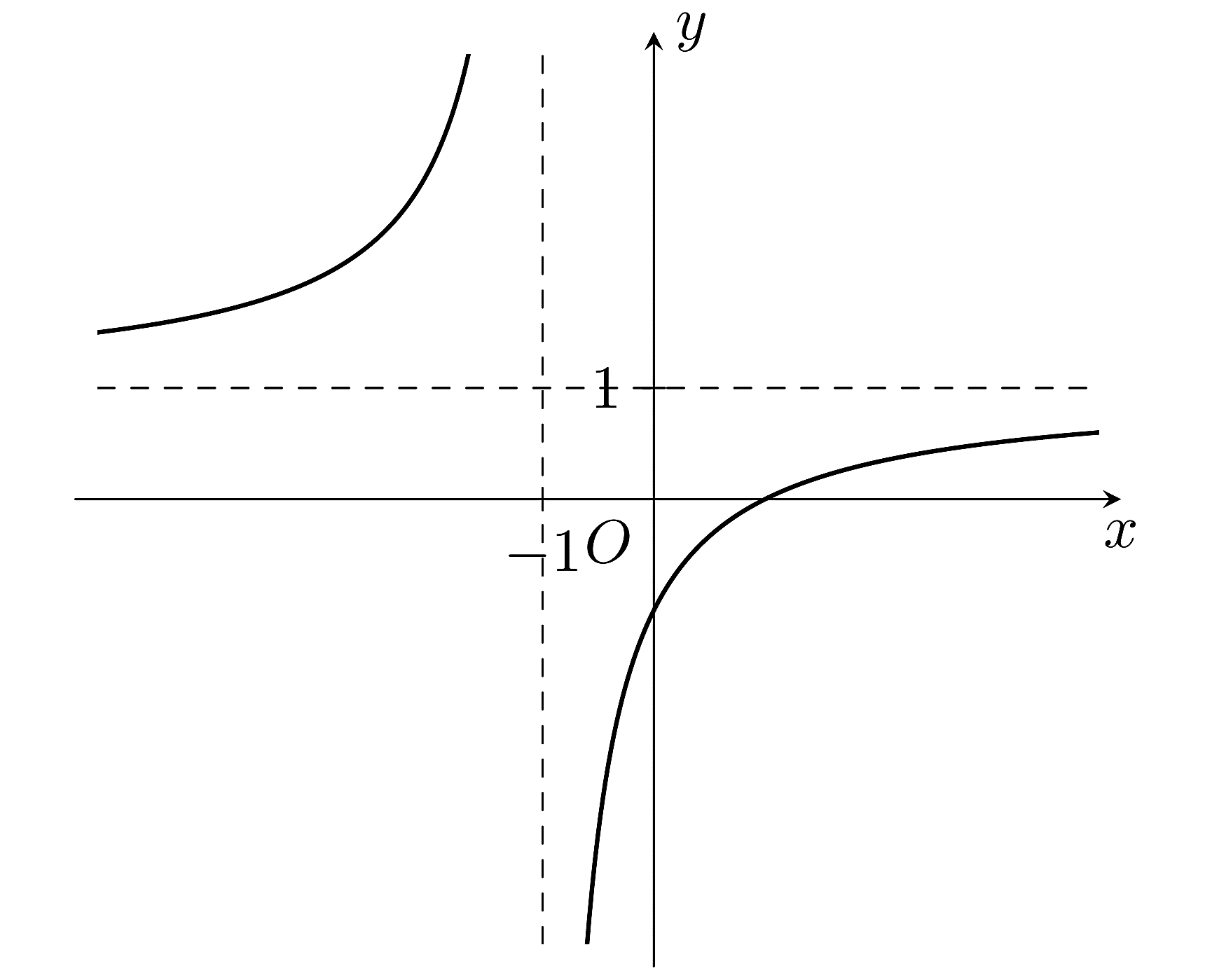
Toạ độ tâm đối xứng của đồ thị hàm số đã cho là:
\[\left( { - 1;1} \right)\].
\[\left( {1;1} \right)\].
\[\left( {1; - 1} \right)\].
\[\left( {0;1} \right)\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới.
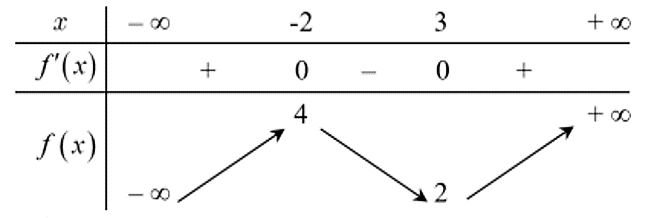
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( { - 1;2} \right)\).
\(\left( { - 8; - 3} \right)\).
\(\left( { - \infty ;4} \right)\).
\(\left( {2; + \infty } \right)\).
Cho hình chóp có diện tích mặt đáy là \(4{a^2}\)và chiều cao bằng \(3a\). Thể tích của khối chóp tương ứng bằng
\(4{a^3}\).
\(12{a^3}\).
\(2{a^3}\).
\(6{a^3}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 3,{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 5\). Gọi \(V\)là thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\)xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
\(V = \int\limits_0^5 {\left( {{x^2} + 3} \right)} \,{\rm{d}}x\).
\(V = \pi \int\limits_0^5 {{{\left( {{x^2} + 3} \right)}^2}} {\rm{d}}x\).
\(V = \int\limits_0^5 {{{\left( {{x^2} + 3} \right)}^2}} {\rm{d}}x\).
\(V = \pi \int\limits_0^5 {\left( {{x^2} + 3} \right)} \,{\rm{d}}x\).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {5; - 4;2} \right)\)và \(B\left( {1;2;4} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với đường thẳng \(AB\) là
\(2x - 3y - z - 20 = 0\).
\(3x - y + 3z - 25 = 0\).
\(3x - y + 3z - 13 = 0\).
\(2x - 3y - z + 8 = 0\).
Tập nghiệm của bất phương trình \(\log x \ge 1\) là:
\(\left[ {10; + \infty } \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( {10; + \infty } \right)\).
\(\left( { - \infty ;10} \right)\).
Khảo sát thời gian tự học ở nhà của học sinh khối 12 ở trường X, ta thu được bảng sau:
|
Thời gian (phút) |
\(\left[ {0;30} \right)\) |
\(\left[ {30;60} \right)\) |
\(\left[ {60;90} \right)\) |
\(\left[ {90;120} \right)\) |
\(\left[ {120;150} \right)\) |
|
Số học sinh tự học |
\(75\) |
\(125\) |
\(250\) |
\(82\) |
\(18\) |
Phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng đơn vị) là
\(874\).
\(872\).
\(873\).
\(875\).
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
\(y = {\log _{\frac{1}{2}}}x\).
\(y = {3^{ - x}}\).
\(y = {2025^x}\).
\(y = {2^x}\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội \(q = 2\). Giá trị của \({u_3}\) bằng
\(12\).
\(18\).
\(7\).
\(6\).
