Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 25)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh \(a\). Giá trị của \(\overrightarrow {AC'} \cdot \overrightarrow {B'D'} \) là:
\(0\).
\( - \frac{1}{2}{a^2}\).
\(\sqrt 6 {a^2}\).
\( - \frac{{\sqrt 2 }}{2}{a^2}\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sin x;y = \cos x\) và các đường thẳng \(x = 0\), \(x = 7\) được tính bằng công thức:
\(S = \int\limits_0^7 {\left( { - \sin x + \cos x} \right){\rm{d}}x} \).
\(S = \int\limits_0^7 {\left| {\sin x - \cos x} \right|{\rm{d}}x} \).
\(S = \int\limits_0^7 {\left( {\sin x - \cos x} \right){\rm{d}}x} \).
\(S = \int\limits_0^7 {\left( {\sin x + \cos x} \right){\rm{d}}x} \).
Khảo sát thời gian tự học của một số học sinh lớp 11 trong một ngày, người ta thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | \(\left[ {0;30} \right)\) | \(\left[ {30;60} \right)\) | \(\left[ {60;90} \right)\) | \(\left[ {90;120} \right)\) | \(\left[ {120;150} \right)\) |
Số học sinh | \(8\) | \(14\) | \(11\) | \(9\) | \(3\) |
Nhóm chứa trung vị của mẫu số liệu trên là
\(\left[ {60;90} \right)\).
\(\left[ {0;30} \right)\).
\(\left[ {30;60} \right)\).
\(\left[ {90;120} \right)\).
Trong không gian \(\left( {Oxyz} \right)\), mặt phẳng \(\left( {Oyz} \right)\) có một vectơ pháp tuyến là
\(\overrightarrow n = \left( {1;1;1} \right)\).
\(\overrightarrow n = \left( {0;0;0} \right)\).
\(\overrightarrow n = \left( {0;1;1} \right)\).
\(\overrightarrow n = \left( {1;0;0} \right)\).
Đồ thị hàm số \[y = - x + 2 + \frac{1}{x}\] có đường tiệm cận xiên là:
\[y = - x + 2\].
\[y = - \frac{1}{x}\].
\(y = x - 2\).
\(y = \frac{1}{x}\).
Tập nghiệm của bất phương trình \[{e^x} > 1\] là:
\[\left( {1\,; + \infty } \right)\].
\[\left( { - \infty \,;0} \right)\].
\[\left( { - \infty ; + \infty } \right)\].
\(\left( {0; + \infty } \right)\).
Tập nghiệm của phương trình \[{\log _4}x = 0\] là:
\[x = - 1\].
\[x = 1\].
\[x = 0\].
\(x = 4\).
Trong không gian với hệ tọa độ \[Oxyz\], phương trình của đường thẳng đi qua hai điểm \[E\left( { - 1;4;2} \right)\]và \[F\left( { - 5\,;0\,;3} \right)\]là:
\[\frac{{x + 1}}{{ - 4}} = \frac{{y - 4}}{{ - 4}} = \frac{{z - 2}}{1}\].
\[\frac{{x + 4}}{{ - 1}} = \frac{{y + 4}}{4} = \frac{{z - 1}}{2}\].
\[\frac{{x - 4}}{{ - 1}} = \frac{{y - 4}}{4} = \frac{{z + 1}}{2}\].
\[\frac{{x - 1}}{{ - 4}} = \frac{{y + 4}}{{ - 4}} = \frac{{z + 2}}{1}\].
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = {\rm{cos}}x + 1\) là:
\({\rm{sin}}x + C\).
\( - {\rm{sin}}x + x + C\).
\({\rm{cos}}x + x + C\).
\({\rm{sin}}x + x + C\).
Cho cấp số cộng \[\left( {{u_n}} \right)\]có \[{u_1} = 1\] và \[{u_2} = - 3\]. Số hạng \[{u_4}\] của cấp số cộng đã cho là
\[ - 11\].
\[ - 27\].
\[ - 7\].
\[ - 14\].
Cho hàm số \[y = {x^3} - 3{x^2} - 2025\]. Hàm số đã cho nghịch biến trên khoảng:
\[\left( {0;2} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( { - \infty ; + \infty } \right)\].
\[\left( {2; + \infty } \right)\].
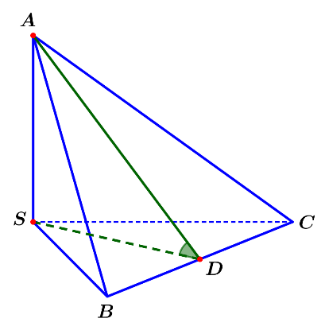
Cho tứ diện \[S.ABC\]có các cạnh \[SA,\,SB,\,SC\]đôi một vuông góc và \[SA = SB = SC = 1\] (minh họa như hình dưới). Gọi \[\alpha \]là góc phẳng nhị diện \[\left[ {S,BC,A} \right]\]. Tính \[\cos \alpha \].
\[\frac{2}{5}\].
\[\frac{{\sqrt 3 }}{3}\].
\[\frac{1}{3}\].
\[\frac{{2\sqrt 5 }}{5}\].
a)Tập xác định của hàm số \(f\left( x \right)\) là khoảng \(\left( { - \frac{1}{4}; + \infty } \right)\).
b)Đạo hàm của hàm số \(f\left( x \right)\) là \(f'\left( x \right) = \frac{{4 \cdot \ln 5}}{{4x + 1}}\).
c) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng xác định của nó.
d) Phương trình tiếp tuyến của đồ thị \(y = f\left( x \right)\) tại điểm \(x = 1\) là \(y = \frac{4}{{5\ln 5}}x - \frac{4}{{5\ln 5}} + 1\).
a) Đường thẳng \[BC\] nằm trong mặt phẳng \[\left( \alpha \right)\].
b) Mặt cầu tâm \[I\left( { - 4;4; - 1} \right)\] tiếp xúc với mặt phẳng \[\left( {ABC} \right)\] có bán kính bằng \[\frac{{26}}{{\sqrt 5 }}\].
c) Đường thẳng \[AB\] có phương trình tham số là \[\left\{ \begin{array}{l}x = 4 + t\\y = - 1 - 2t\\z = 2 - 3t\end{array} \right.\].
d) Với điểm \[M \in \left( \alpha \right)\] thì giá trị nhỏ nhất của biểu thức \[\left| {\overrightarrow {MA} - 4\overrightarrow {MB} - 3\overrightarrow {MC} } \right|\] bằng \[\frac{3}{{\sqrt {21} }}\].
a) \(P\left( A \right) = 0,7.\)
b) \(P\left( B \right) = 0,8.\)
c) \(P\left( C \right) = 0,04.\)
d) \(P\left( D \right) = 0,76.\)
a) Tốc độ gia tăng dân số của khu vực \[A\] với \[t = 4\] là 8 000.
b) Ta có \[{P'_A}\left( 0 \right) = 8\]và \[a = 8\].
c) Dân số khu vực \[A\] tăng thêm từ 0 đến 5 năm là 33 000 (người).
d) Phần diện tích tô đậm trong hình vẽ biểu diễn sự chênh lệch dân số tăng thêm giữa hai khu vực trong giai đoạn từ 0 đến 5 năm là 9 000 người.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Gọi \[M\left( {a;b} \right)\] là điểm thuộc đồ thị hàm số \[y = \frac{{2x + 1}}{{x + 2}}\] và có khoảng cách từ \[M\] đến đường thẳng \[d:y = 3x + 6\] nhỏ nhất. Tính giá trị của biểu thức \[T = 6{a^2} + 7{b^2}.\]
Thống kê thời gian tự học môn Toán của 400 học sinh lớp 12 trong một ngày ta được kết quả trong bảng ghép nhóm sau:
Thời gian (phút) | \[\left[ {0;20} \right)\] | \[\left[ {20;40} \right)\] | \[\left[ {40;60} \right)\] | \[\left[ {60;80} \right)\] | \[\left[ {80;100} \right)\] |
Số học sinh | \[x\] | 120 | \[y\] | 70 | 60 |
Biết rằng \[x,y\] là các số nguyên dương và khoảng tứ phân vị của mẫu số liệu bằng \[\frac{{845}}{{21}}\]. Khi đó, thời gian tự học trung bình của 400 học sinh (tính theo mẫu số liệu ghép nhóm trên) là bao nhiêu phút?
Chạy Marathon là môn thể thao chạy bộ đường dài mà tại đó, người chơi sẽ hoàn thành quãng đường 42,195 km trong khoảng thời gian nhất định. “FM sub 4” là một thuật ngữ phổ biến trong cộng đồng những người tham gia chạy Marathon, nó dùng để chỉ thành tích hoàn thành quãng đường 42,195 km dưới 4 giờ. Trong một câu lạc bộ Marathon, tỉ lệ thành viên nam là 72%, tỉ lệ thành viên nữ là 28%. Đối với nam, tỉ lệ người hoàn thành FM sub 4 là 32%; đối với nữ, tỉ lệ người hoàn thành FM sub 4 là 3%. Chọn ngẫu nhiên một người từ câu lạc bộ đó. Xác suất để người được chọn là nam bằng bao nhiêu (kết quả được làm tròn đến hàng phần trăm), biết rằng người được chọn đã hoàn thành FM sub 4?
Mộtbể bơi ban đầu có dạng hình hộp chữ nhật \(ABCD.A'B'C'D'\). Sau đó người ta làm lại mặt đáy như hình vẽ. Biết rằng \(A'B'MN\) và \(MNEF\) là các hình chữ nhật, \(\left( {MNFE} \right){\rm{//}}\left( {A'B'C'D'} \right)\), \(AB = 10\,{\rm{m}}\), \(AD = 30\,{\rm{m}}\), \(AA' = 20\,{\rm{m}}\), \(MF = DE = 17\,{\rm{m}}\).Tính tỉ số thể tích của bể sau khi làm lại mặt đáy với thể tích của bể lúc ban đầu (Kết quả làm tròn đến hàng phần trăm).
Trong giờ thể dục học về kỹ thuật chuyền bóng hơi, Bình và An tập chuyền bóng cho nhau. Ở một động tác Bình chuyền bóng cho An, quả bóng bay lên cao nhưng lại lệch sang bên trái của An và rơi xuống vị trí cách chỗ An đứng \[0,5\,{\rm{m}}\] và cách chỗ Bình \[4,5\,{\rm{m}}\]. Chọn hệ trục tọa độ \[Oxyz\] sao cho gốc tọa độ \[O\] tại vị trí của Bình, vị trí của An nằm trên tia \[Ox\] và mặt phẳng \[Oxy\] là mặt đất (tham khảo hình vẽ).
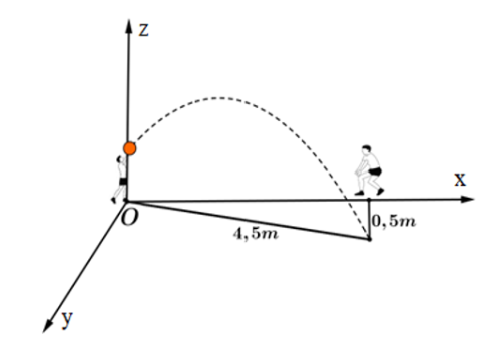
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng \[\left( \alpha \right):x + by + cz + d = 0\] và \[\left( \alpha \right)\] vuông góc với mặt đất. Khi đó, giá trị của \[ - 5{b^2} - {c^2} + 3{d^2}\] bằng bao nhiêu?
Nhằm thu hút du khách và khẳng định vị thế dẫn đầu, công viên nước Đầm Sen quyết định đầu tư xây dựng một đường trượt nước độc đáo có mặt cắt được gắn vào hệ trục \(Oxy\) (xem trục \(Ox\) là mặt đất) với đơn vị mỗi trục là \(1\,{\rm{m}}\) như hình vẽ dưới đây. Đường trượt được thiết kế theo hình dạng của một hàm bậc ba \(y = g\left( x \right)\), với mục tiêu tối ưu hóa trải nghiệm của người dùng , một phần đường trượt được đặt dưới mặt đất để tận dụng địa hình và tạo hiệu ứng bất ngờ. Điểm đầu của đường trượt là \(H\left( { - 3;a} \right)\) và điểm cuối là \(K\left( {8;0} \right)\) và ngay dưới điểm \(K\) là một bể bơi. Để tiếp cận đường trượt, một cầu thang cong có dạng parabol \(y = f\left( x \right)\) có đỉnh là điểm \(M\left( { - 8;0} \right)\) được xây dựng, đảm bảo độ dốc vừa phải và an toàn cho người sử dụng.
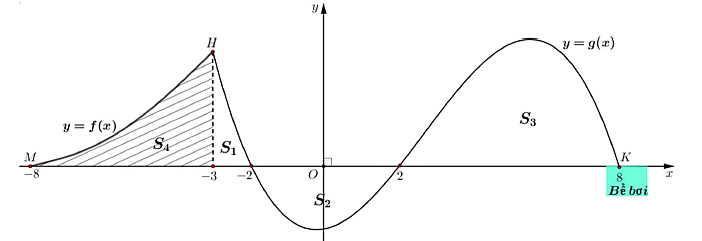
Các diện tích hình phẳng được tạo bởi các đồ thị \(y = f\left( x \right),y = g\left( x \right),x = - 3\) và trục hoành như hình vẽ. Để đảm bảo an toàn tuyệt đối cho người chơi và tính ổn định của công trình, các kỹ sư cần đặc biệt chú trọng đến phần đường trượt nằm dưới lòng đất. Hãy xác định độ cao lớn nhất mà đường trượt chìm xuống so với mặt đất (đơn vị: mét) biết rằng \({S_1} + {S_3} = {S_2} + {S_4} + \frac{{109}}{{12}}\) (làm tròn kết quả đến hàng phần trăm).




