Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 23)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) là hàm đa thức có đạo hàm \(f'\left( x \right) = x\left( {{x^2} - 1} \right){\left( {x - 2} \right)^2}\). Số điểm cực tiểu của đồ thị hàm số là:
\[1\].
\[4\].
\[3\].
\[2\].
Với \(a,b\) là các số thực dương tùy ý, gọi \(x = {\log _2}a,y = {\log _2}b,P = {\log _2}\left( {{a^2}{b^3}} \right)\). Khẳng định nào sau đây là đúng?
\(P = {x^2}{y^3}\).
\(P = {x^2} + {y^3}\).
\(P = 2x + 3y\).
\(P = 6xy\).
Các nghiệm của phương trình \[\cos 2x = 0\] là
\(x = \frac{\pi }{2} + k\pi \,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{8} + \frac{{k\pi }}{2}\,\left( {k \in \mathbb{Z}} \right)\).
\(x = k\frac{\pi }{2}\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k\frac{\pi }{2}\,\left( {k \in \mathbb{Z}} \right)\).
Trong không gian \[Oxyz\], cho đường thẳng \(d:\frac{{x - 3}}{2} = \frac{{y - 4}}{{ - 5}} = \frac{{z + 5}}{3}\). Điểm nào sau đây thuộc đường thẳng \(d\)?
\[M\left( {3;4; - 5} \right)\].
\[N\left( {2; - 5;3} \right)\].
\[P\left( { - 3; - 4;5} \right)\].
\[Q\left( {2;5; - 3} \right)\].
Tập nghiệm của bất phương trình \({\left( {\frac{3}{4}} \right)^{2x - 1}} \le {\left( {\frac{4}{3}} \right)^{ - 2 + x}}\) là:
\(S = \left( { - \infty ;1} \right]\).
\(S = \left( {1; + \infty } \right)\).
\(S = \left[ {1; + \infty } \right)\).
\(S = \left( { - \infty ;1} \right)\).
Bảng sau đây biểu diễn mẫu số liệu ghép nhóm thống kê về nhu cầu mức giá mua nhà (đơn vị triệu đồng\({\rm{/}}{{\rm{m}}^{\rm{2}}}\)) của khách hàng tại một công ty xây dựng:
Nhóm | \(\left[ {10;14} \right)\) | \(\left[ {14;18} \right)\) | \(\left[ {18;22} \right)\) | \(\left[ {22;26} \right)\) | \(\left[ {26;30} \right)\) |
Tần số | \[54\] | \(78\) | \(120\) | \(45\) | \(12\) |
Khoảng biến thiên của một số liệu ghép nhóm trên là:
\(9\).
\(4\).
\(20\).
\(108\).
Công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và 2 đường thẳng \(x = a,x = b\left( {a < b} \right)\), xung quanh trục \(Ox\) là:
\(V = \int\limits_a^b {{f^2}\left( x \right){\rm{d}}x} \).
\(V = \pi \int\limits_a^b {f\left( x \right){\rm{d}}x} \).
\(V = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \).
\(V = \pi \int\limits_a^b {{f^2}\left( x \right){\rm{d}}x} \).
Chohàm số có đồ thị như hình vẽ dưới đây.
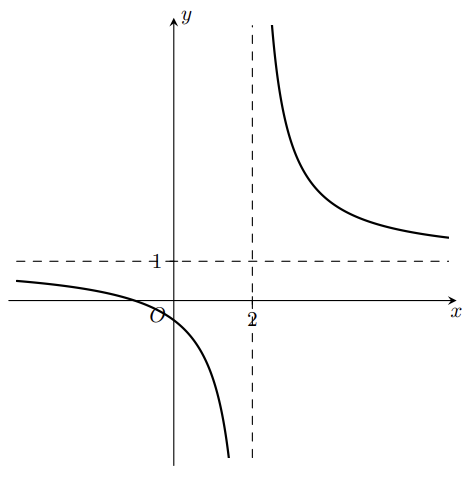
Đồ thị hàm số có tiệm cận ngang là:
\(y = 1\).
\(y = 2\).
\(x = 1\).
\(x = 2\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Góc giữa hai đường thẳng nào sau đây bằng \(90^\circ \)?
\(SA,SB\).
\(SB,AD\).
\(SA,BD\).
\(SA,SC\).
Trong không gian \[Oxyz\], mặt phẳng nào dưới đây nhận vectơ \(\overrightarrow n = \left( {3;1; - 7} \right)\) làm một vectơ pháp tuyến?
\(3x - y - 7z + 1 = 0\).
\(3x + z + 7 = 0\).
\(3x + y - 7z - 3 = 0\).
\(3x + y - 7 = 0\).
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Mệnh đề nào sau đây đúng?
\(\left| {\overrightarrow {BA} + \overrightarrow {B{B_1}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {B{D_1}} } \right|\).
\(\left| {\overrightarrow {A{A_1}} + \overrightarrow {{C_1}D} + \overrightarrow {{C_1}{D_1}} } \right| = 0\).
\(\left| {\overrightarrow {A{B_1}} - \overrightarrow {A{D_1}} } \right| = \left| {\overrightarrow {B{D_1}} } \right|\).
\(\left| {\overrightarrow {A{B_1}} + \overrightarrow {A{D_1}} } \right| = \left| {\overrightarrow {A{C_1}} } \right|\).
Biết \(\int\limits_1^3 {f\left( x \right){\rm{d}}x = 5} \) và \(\int\limits_1^3 {g\left( x \right){\rm{d}}x = - 7} \). Giá trị của \(\int\limits_1^3 {\left[ {3f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} \) bằng
\( - 31\).
\(29\).
\(1\).
\( - 29\).
a) Nồng độ khí \(C{O_2}\) trong phòng tại thời điểm \(t = 0\) là 400 \(\left( {{\rm{ppm}}} \right)\).
b) \(f'\left( t \right) = \frac{{ - 2000{t^2} - 10000}}{{{{\left( {{t^2} + 5} \right)}^2}}}\) với \(t \ge 0\).
c) Nghiệm của phương trình \[f'\left( t \right) = 0\] là \(t = 2\).
d) Nồng độ khí \(C{O_2}\) cao nhất đo được trong phòng thí nghiệm (làm tròn kết quả đến hàng đơn vị) là 947 \(\left( {{\rm{ppm}}} \right)\).
a) Hàm số \(V\left( t \right)\) là một nguyên hàm của hàm số \(f\left( t \right) = k \cdot \sqrt t \).
b) \(V\left( t \right) = \frac{{2k}}{3} \cdot t\sqrt t + C,\) với \(0 \le t \le 24\) và \(k,\,C\) là các hằng số.
c) Sau 16 giờ bơm liên tục, thể tích dầu trong bể đạt được là 148 000 lít.
d) Trong quá trình bơm dầu, nếu sau mỗi giờ lượng dầu bị rò rỉ đều đặn với tốc độ 500 lít/giờ, thì tại thời điểm \(t\) bằng 9 giờ, thể tích dầu trong bể là 72 000 lít.
a) Xác suất để người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \[\frac{{33}}{{50}}\].
b) Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[\frac{{13}}{{20}}\], biết rằng người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng.
c) Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[\frac{{33}}{{50}}\].
d) Để tạo bất ngờ cho người bốc thăm tiếp theo, sau khi người thứ nhất bốc thăm, người dẫn chương trình giữ lại vé và không công bố kết quả. Người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng. Xác suất để người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \[\frac{{65}}{{99}}\].
a) Phương trình đường thẳng \(AB\) là \(\left\{ \begin{array}{l}x = 4 - 3t\\y = - 5 + 7t\\z = 1 - t\end{array} \right.\).
b) Góc trượt (góc giữa đường bay \(AB\) và mặt đất là mặt phẳng nằm ngang \(\left( {Oxy} \right)\)) không nằm trong phạm vi cho phép từ \(2,5^\circ \) đến \(9^\circ \).
c) Có một lớp mây mô phỏng bởi mặt phẳng \(\left( P \right)\) đi qua ba điểm \(M\left( {5;0;0} \right),\,\,N\left( {0; - 1;0} \right),\)\(P\left( {0;0;2} \right)\). Máy bay xuyên qua đám mây tại điểm \(C\) có cao độ làm tròn đến hàng đơn vị là \(346\,{\rm{m}}\).
d) Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là \(800\,{\rm{m}}\). Sau khi ra khỏi đám mây, người phi công đạt được quy định an toàn bay là người phi công phải nhìn thấy điểm đầu \(E\left( {2;0,5;0} \right)\) của đường băng ở độ cao tối thiểu \(150\,{\rm{m}}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty trung bình bán được 600 chiếc máy lọc không khí mỗi tháng với giá 10 triệu đồng một chiếc. Một khảo sát cho thấy nếu giảm giá bán mỗi chiếc 400 nghìn đồng, thì số lượng bán ra tăng thêm khoảng 60 chiếc mỗi tháng. Gọi \(p\) (triệu đồng) là giá bán của mỗi máy, \(x\) là số máy bán ra. Khi đó, hàm cầu \(p = p\left( x \right)\)và hàm doanh thu là \(R\left( p \right) = px\). Hỏi công ty phải bán mỗi máy lọc không khí với số tiền bao nhiêu triệu đồng để doanh thu là lớn nhất?
Một tòa nhà có hình dạng là một hình chóp tứ giác đều có cạnh đáy là \(160\,{\rm{m}}\) và cạnh bên là \(140\,{\rm{m}}\). Giả sử, từ một mặt bên của tòa nhà ta cần thiết kế con đường ngắn nhất để di chuyển đến tâm của đáy tòa nhà, khi đó quãng đường ngắn nhất có độ dài khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?
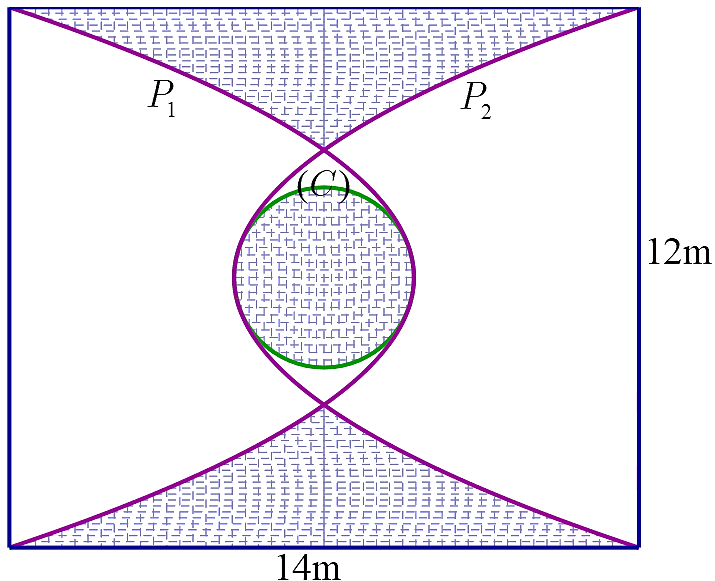
Người ta lát gạch trang trí một mảnh sân hình chữ nhật có kích thước \[14{\rm{m}} \times 12{\rm{m}}\] như hình vẽ dưới, trong đó \[\left( {{P_1}} \right),\,\,\left( {{P_2}} \right)\] là hai parabol đối xứng trục với nhau qua trục đối xứng vuông góc với chiều dài của mảnh sân, \[\left( C \right)\] là đường tròn có tâm trùng với tâm của mảnh sân và lần lượt có duy nhất một điểm chung với các parabol đó (tham khảo hình vẽ biết phần gạch đậm là phần lát gạch). Chi phí cho phần lát gạch là \[240\] nghìn đồng một mét vuông. Trong trường hợp hình tròn \[\left( C \right)\] có diện tích lớn nhất thì chi phí lát gạch là bao nhiêu triệu đồng? (kết quả làm tròn tới hàng phần chục).
Có hai người gọi điện thoại đến hai số điện thoại khác nhau nhưng đều quên mất chữ số cuối. Họ đều thử ngẫu nhiên các chữ số từ 0 đến 9 và không lặp lại các số đã thử. Tính xác suất để ít nhất một trong hai người đó gọi đúng số điện thoại đã quên mà không phải thử quá hai lần.
Trong không gian\[Oxyz\] (đơn vị trên mỗi trục tọa độ là mét), một ngôi nhà như hình vẽ dưới đây có sàn nhà nằm ngang trên mặt phẳng \[\left( \alpha \right):2x + y - 3z + 18 = 0\]. Hai mái nhà lần lượt nằm trên các mặt phẳng \[\left( P \right):x - y = 0\], \[\left( Q \right):x + y - 2z = 0\]. Hỏi chiều cao của ngôi nhà tính từ sàn nhà đến nóc nhà (điểm cao nhất của mái nhà) là bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?
Trong lần đầu tiên nuôi gà, một trang trại do thiếu kinh nghiệm nên dự tính lượng thức ăn cho gà hằng ngày là không đổi và đã dự trữ thức ăn đủ dùng trong \[50\] ngày. Nhưng thực tế, theo sự phát triển của gà, để đảm bảo chất lượng thì kể từ ngày thứ 2 trở đi lượng thức ăn nuôi gà mỗi ngày của trang trại đã tăng thêm \[1\% \] so với ngày trước đó. Hỏi lượng thức ăn mà trang trại dự trữ đủ dùng cho gà ăn tối đa bao nhiêu ngày mà vẫn đảm bảo chất lượng ăn mỗi ngày? (lấy kết quả số ngày là số nguyên).




