Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 22)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Trọng lượng của 20 củ sâm trong một lô củ sâm được thu hoạch sau sáu năm trồng tại một cơ sở trồng sâm có bảng tần số ghép nhóm sau (đơn vị: gam):
Nhóm | \(\left[ {40;45} \right)\) | \(\left[ {45;50} \right)\) | \(\left[ {50;55} \right)\) | \(\left[ {55;60} \right)\) |
Tần số | \(3\) | \(7\) | \(8\) | \(2\) |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:
\(3,3\).
\(9,5\).
\(6,7\).
\(8,6\).
Tập nghiệm của bất phương trình \({3^{x - 2}} > 9\) là:
\(\left( { - \infty ;2} \right)\).
\(\left( {4; + \infty } \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( {5; + \infty } \right)\).
Trong không gian \(Oxyz\), cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 - 2t}\\{y = 3 + t}\\{z = - 1 + 4t}\end{array}} \right.\). Điểm nào dưới đây thuộc đường thẳng \(d\)?
\(P\left( { - 1; - 3;1} \right)\).
\(M\left( {1;3; - 1} \right)\).
\(N\left( { - 2;2;4} \right)\).
\(Q\left( { - 1;1;2} \right)\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết hàm số \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) và \(F\left( 3 \right) = 5,F\left( 1 \right) = 1\). Tích phân \(\int\limits_1^3 {f\left( x \right){\rm{d}}x} \) bằng:
\( - 4\).
\(5\).
\(6\).
\(4\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong như hình vẽ dưới đây.
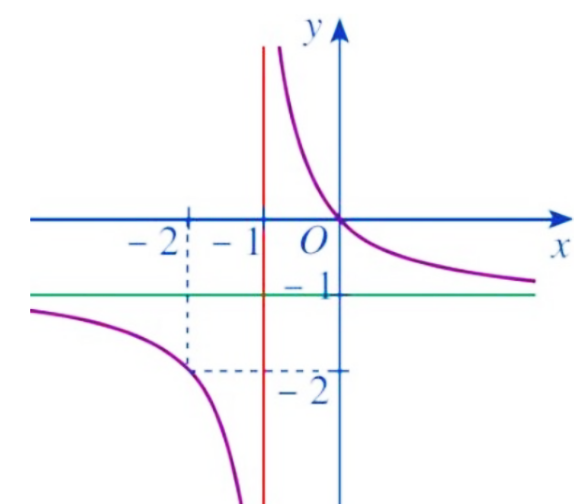
Hàm số nghịch biến trên khoảng (các khoảng) nào sau đây?
\(\left( { - 2;0} \right)\).
\(\left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
\(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
Nghiệm của phương trình\({\log _2}x = 3\) là
\(x = \frac{3}{2}\).
\(x = 8\).
\(x = 6\).
\(x = 5\).
Cho cấp số cộng \(\left( {{u_n}} \right)\)có \({u_1} = - 3,{u_6} = 27\). Công sai \(d\) của cấp số cộng đã cho là:
\[d = 8\].
\[d = 5\].
\[d = 7\].
\[d = 6\].
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\sqrt 2 \). Tam giác \(ABC\) vuông cân tại \(B\) và \(AB = a\). Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng
\(60^\circ \).
\(30^\circ \).
\(45^\circ \).
\(90^\circ \).
Cho đồ thị hàm số như hình dưới đây.
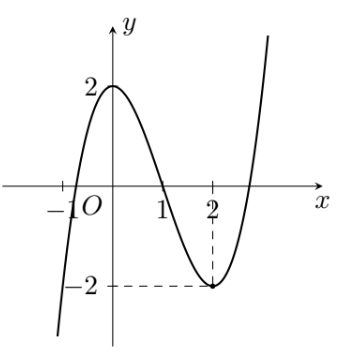
Hàm số đó là hàm số nào?
\(y = \frac{{x + 1}}{{x + 2}}\).
\(y = - {x^3} - 6x + 2\).
\(y = - {x^3} + 3{x^2} + 2\).
\(y = {x^3} - 3{x^2} + 2\).
Trong không gian \(Oxyz\), mặt cầu \(\left( S \right)\) có phương trình \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 4\) có bán kính bằng
\(16\).
\(8\).
\(2\).
\(4\).
Khẳng định nào dưới đây đúng?
\(\int {{{2025}^x}{\rm{d}}x} = \frac{{{{2025}^{x + 1}}}}{{x + 1}} + C\).
\(\int {{{2025}^x}{\rm{d}}x} = \frac{{{{2025}^{x + 1}}}}{{\ln 2025}} + C\).
\(\int {{{2025}^x}{\rm{d}}x} = {2025^x} \cdot \ln 2025 + C\).
\(\int {{{2025}^x}{\rm{d}}x} = \frac{{{{2025}^x}}}{{\ln 2025}} + C\).
Cho hình chóp có diện tích mặt đáy là \(3{a^2}\) và chiều cao bằng \(6a\). Thể tích của khối chóp bằng:
\(18{a^3}\).
\(6{a^3}\).
\(9{a^3}\).
\(3{a^3}\).
a) Đạo hàm của hàm số đã cho là \(y' = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
b) Đường thẳng \(AB\) có phương trình là \(y = 2x + 1\).
c) Hai điểm \(A\) và \(B\) nằm ở hai phía trục tung.
d) Hai điểm \(A,B\) đối xứng nhau qua đường thẳng \(\Delta \) có phương trình \(x + 2y + 4 = 0\).
a) Lợi nhuận khi bán được \(50\) sản phẩm đầu tiên là \(519\) triệu đồng.
b) Biết sự thay đổi của lợi nhuận khi doanh số tăng từ \(50\) lên \(a\) đơn vị sản phẩm lớn hơn \(517\) triệu đồng, khi đó giá trị nhỏ nhất của \(a\) là \(100\).
c) Lợi nhuận khi bán được \(x\) đơn vị sản phẩm được tính bằng công thức
\(P\left( x \right) = - 0,0008{x^2} + 10,4x\).
d) Sự thay đổi của lợi nhuận khi doanh số tăng từ \(50\) lên \(55\) đơn vị sản phẩm là \(51,79\) triệu đồng.
a) Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là 0,343.
b) Xác suất trong 3 sinh viên có ít nhất 1 sinh viên không dùng cà phê là 0,657.
c) Xác suất trong 3 sinh viên có đúng 1 sinh viên dùng cà phê là 0,189.
d) Xác suất trong 3 sinh viên có đúng 2 sinh viên dùng cà phê và 1 sinh viên không dùng cà phê lớn hơn 0,45.
a) Tọa độ của điểm \(A\left( {8;\,3;\,10} \right)\).
b) Phương trình đường thẳng đi qua vị trí của hai chiếc flycam tại \(A\) và \(B\) là \(\left\{ \begin{array}{l}x = 8 + 12t\\y = 3 + 8t\\z = 10 - 2t\end{array} \right.\).
c) Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua \(M\left( {1;\,2;\, - 1} \right)\).
d) Trên mặt đất người ta đặt một thiết bị phá sóng flycam sao cho có thể phá sóng hai chiếc flycam tại hai vị trí \(A,\,\,B\) cùng một lúc. Tổng khoảng cách ngắn nhất từ thiết bị đó đến hai chiếc flycam tại hai vị trí \(A\) và \(B\) (làm tròn kết quả đến hàng phần trăm) bằng \(25,46\,\,{\rm{(m)}}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Trong Vật lý, một dao động điều hòa là dao động có phương trình chuyển động \(x\left( t \right) = A\cos \left( {\omega t + \varphi } \right)\) trong đó \(A\) là biên độ của dao động, \(\omega \,\,\left( {{\rm{rad/s}}} \right)\) là tần số góc, \(\varphi \,\left( {{\rm{rad}}} \right)\) là pha ban đầu. Động năng (Tiếng Anh: Kinetic energy) của một vật là năng lượng nó có được từ chuyển động của nó, được xác định bởi công thức \(W = \frac{1}{2}m \cdot {v^2}\left( t \right)\) (đơn vị Jun (J)). Trong đó \(m\,\,\left( {{\rm{kg}}} \right)\) là khối lượng của vật, \(v\left( t \right)\,\,\left( {{\rm{m/s}}} \right)\) là vận tốc của vật tại thời điểm \(t\,\left( {\rm{s}} \right)\). Giả sử một vật có khối lượng \(m = 100\,\,{\rm{g}}\)dao động điều hòa với phương trình chuyển động \(x\left( t \right) = 40\cos \left( {200\pi t - \frac{\pi }{3}} \right)\,\,\left( {{\rm{cm}}} \right)\). Khi đó, động năng vật đó đạt giá trị lớn nhất bằng bao nhiêu Jun (làm tròn kết quả đến hàng đơn vị)?
Cho khối chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang vuông tại \[A\] và \[B,AB = BC = 1,\]\[AD = 2.\] Hình chiếu vuông góc của \[S\] lên mặt phẳng đáy trùng với trung điểm \[H\] của \[AD\] và \[SH = \frac{{\sqrt 6 }}{2}.\] Tính khoảng cách từ \[B\] đến mặt phẳng \[\left( {SCD} \right)\] (làm tròn kết quả đến hàng phần trăm).
Hai nhà máy sản xuất đặt tại các vị trí \(A\) và \(B\)cách nhau \(4\,\,{\rm{km}}\). Một nhà máy cung cấp nước được đặt ở vị trí \(C\) nằm trên đường trung trực của đoạn thẳng \(AB\), cách trung điểm \(M\)của đoạn thẳng \(AB\) một khoảng \(4\,\,{\rm{km}}\). Người ta muốn làm một đường ống dẫn nước từ nhà máy nước \(C\)đến một vị trí \(I\)nằm giữa đoạn thẳng \(MC\)sau đó chia ra hai nhánh dẫn tới hai nhà máy \(A\) và \(B\)(hình vẽ).
Tổng độ dài đường ống dẫn nước nhỏ nhất bằng bao nhiêu kilômét? (làm tròn kết quả đến hàng phần trăm).

Nam và ba người bạn lên kế hoạch cho một chuyến đi phượt xuyên Việt, ghé thăm 4 thành phố: A, B, C và D. Họ xuất phát từ A, đi qua tất cả các thành phố còn lại đúng một lần rồi quay về A. Bảng chi phí nhiên liệu (tính bằng lít xăng) giữa các thành phố như sau:
| A | B | C | D |
A | 0 | 40 | 90 | 110 |
B | 40 | 0 | 50 | 70 |
C | 90 | 50 | 0 | 30 |
D | 110 | 70 | 30 | 0 |
Xe của nhóm hiện đã có sẵn \(150\)lít xăng. Để hoàn thành hành trình, họ cần đổ thêm ít nhất bao nhiêu lít xăng?
Một căn bệnh có 1% dân số mắc phải. Một phương pháp chẩn đoán căn bệnh nói trên có tỉ lệ chính xác là 98% (với cả người bị bệnh và người không bị bệnh). Biết rằng nếu một người được sử dụng phương pháp trên để kiểm tra và cho kết quả dương tính (bị bệnh) thì xác suất người đó thực sự bị bệnh là \(\frac{y}{{148}},\)\(y\) là số tự nhiên. Hỏi \(y\) bằng bao nhiêu?
Trạm tàu cứu hộ được đặt tại vị trí \(A\left( {5;0;0} \right)\) trên một hòn đảo nhỏ trong không gian \(Oxyz\)(đơn vị trên mỗi trục được tính bằng km), được sử dụng làm trạm cứu hộ, cứu nạn trên biển. Tàu du lịch B đang di chuyển (vận tốc không đổi) trên tuyến đường được mô tả bởi đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1 + t{\rm{ }}}\\{y = 3 - 2t}\\{z = 0{\rm{ }}}\end{array}} \right.\). Tàu chở hàng C đang di chuyển (vận tốc không đổi) trên tuyến đường vận tải được mô tả bởi đường thẳng \({d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 - s}\\{y = 9 + s}\\{z = 0{\rm{ }}}\end{array}} \right.\). Do thời tiết xấu, nên tàu B và C gặp sự cố và cần được tiếp cận khẩn cấp. Trạm cứu hộ điều một tàu cứu hộ xuất phát từ A để lần lượt tiếp cận tàu du lịch B trước, sau đó đến tàu chở hàng C. Xét vị trí tối ưu của tàu du lịch B dừng lại và tàu chở hàng C dừng lại sao cho tổng quãng đường tàu cứu hộ cần đi \(P = AB + BC + CA\) là nhỏ nhất. Khi đó \({P_{\min }} = \sqrt a \) (km), hãy tính \(a + 2025?\)




