Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 21)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho cấp số nhân \[\left( {{u_n}} \right)\]với \[{u_1} = 3\] và công bội \[q = - 2\]. Giá trị của \[{u_4}\] bằng
\(24\).
\( - 12\).
\( - 24\).
\(12\).
Cho hàm số\[y = f\left( x \right)\] xác định trên \[\mathbb{R}\]và có bảng biến thiên như sau:
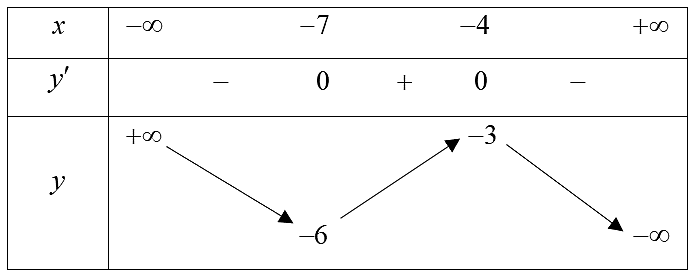
Điểm cực đại của hàm số \[y = f\left( x \right)\] là
\[x = - 7\].
\[x = - 6\].
\[x = - 3\].
\[x = - 4\].
Nguyên hàm \[F\left( x \right)\] của hàm số \[f\left( x \right) = \frac{1}{x} + e\] là
\[F\left( x \right) = - \frac{1}{{{x^2}}} + {e^x} + C\].
\[F\left( x \right) = \ln \left| x \right| + ex + C\].
\[F\left( x \right) = \ln \left| x \right| + {e^x} + C\].
\[F\left( x \right) = \ln x + e + C\].
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):2x + y - 1 = 0\) có một vectơ pháp tuyến là
\({\vec n_1} = \left( { - 2; - 1;1} \right)\).
\({\vec n_2} = \left( {2;1; - 1} \right)\).
\({\vec n_3} = \left( {1;2;0} \right)\).
\({\vec n_4} = \left( {2;1;0} \right)\).
Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau:
Lượng nước tiêu thụ (m3) | \(\left[ {3\,;\,6} \right)\) | \(\left[ {6\,;\,9} \right)\) | \(\left[ {9\,;\,12} \right)\) | \(\left[ {12\,;\,15} \right)\) | \(\left[ {15\,;\,18} \right)\) |
Số hộ gia đình | \(20\) | \(60\) | \(40\) | \(32\) | \(7\) |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
\[20\,\,{{\rm{m}}^{\rm{3}}}\].
\[18\,\,{{\rm{m}}^{\rm{3}}}\].
\[3\,\,{{\rm{m}}^{\rm{3}}}\].
\[15\,\,{{\rm{m}}^{\rm{3}}}\].
Cho hàm số \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\]. Biết \[F\left( 1 \right) = - 3,F\left( { - 2} \right) = 12\]. Tính \[I = \int\limits_{ - 2}^1 {f\left( x \right)} \,{\rm{d}}x\].
\[I = 9\].
\[I = 15\].
\[I = - 36\].
\[I = - 15\].
Cho hai biến cố độc lập \[A\] và \[B\]với \[P\left( A \right) = 0,7;\,P\left( B \right) = 0,2\]. Khi đó, \[P\left( {A|B} \right)\]bằng:
\(0,3\).
\[0,7\].
\(0,8\).
\(0,2\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {1;5} \right]\) và có đồ thị như hình vẽ sau:
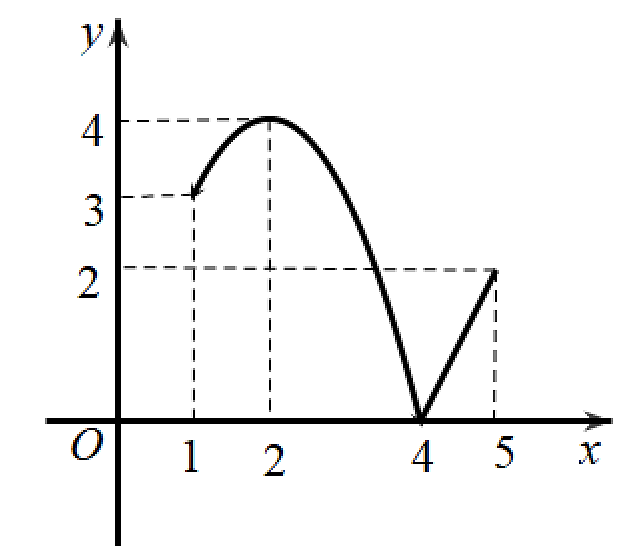
Trên đoạn \(\left[ {1;5} \right]\), hàm số đã cho đạt giá trị lớn nhất tại điểm
\(x = 4\).
\(x = 1\).
\(x = 2\).
\(x = 5\).
Tập nghiệm của bất phương trình \({\rm{lo}}{{\rm{g}}_{\frac{1}{2}}}\left( {x + 1} \right) > - 1\) là
\(\left( { - 1;1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( {0;3} \right)\).
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - 2x - 1}}{{x - 2}}\) là
\(y = - 2\).
\(y = 2\).
\(x = 2\).
\(x = - 2\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Cạnh \(SA\) vuông góc với mặt phẳng đáy và có độ dài là \(2a\). Thể tích khối chóp \(S.BCD\) bằng
\(\frac{{{a^3}}}{8}\).
\(\frac{{{a^3}}}{3}\).
\(\frac{{{a^3}}}{4}\).
\(\frac{{2{a^3}}}{3}\).
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) có phương trình \({x^2} + {y^2} + {z^2} = \frac{1}{4}\). Bán kính \(R\) của mặt cầu \(\left( S \right)\) bằng
\(R = \frac{1}{2}\).
\(R = \frac{1}{4}\).
\(R = 2\).
\(R = 4\).
a) Hàm số có 2 điểm cực trị.
b) Hàm số nghịch biến trên khoảng \[\left( {0\,;2} \right)\].
c) Đồ thị \[\left( C \right)\] có tiệm cận đứng là đường thẳng có phương trình \(x = 1\).
d) \[M\]là điểm bất kì thuộc đồ thị \[\left( C \right)\]. Tích khoảng cách từ \[M\]đến tiệm cận đứng và tiệm cận xiên của đồ thị \[\left( C \right)\] bằng \[\sqrt 2 \].
a) Phương trình parabol \[\left( P \right)\] là \[v\left( t \right) = 2{t^2} - 8t + 10\].
b) Quãng đường vật di chuyển được trong khoảng thời gian từ \(0\)giây đến \(5\) giây là \[\frac{{115}}{3}\,\,{\rm{(m)}}\].
c) Quãng đường vật di chuyển được trong khoảng thời gian từ giây thứ 5 đến giây thứ 10 là \[\frac{{385}}{2}\,\,{\rm{(m)}}\].
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[v\left( t \right),\]trục \[Ot\], và hai đường thẳng \[t = 0,t = 10\] là \[\frac{{395}}{6}\] (đvdt).
a) Xác suất để chọn được một nam là \(\frac{5}{9}\).
b) Xác suất để chọn được một người có việc làm là \(\frac{2}{3}\).
c) Tại địa phương này, nếu chỉ có bằng tốt nghiệp THPT thì tỉ lệ nữ thất nghiệp sẽ cao hơn nam. Khảo sát cho thấy xác suất để một người thất nghiệp khi người đó là nữ cao gấp 7 lần xác suất để một người thất nghiệp khi người đó là nam.
d) Biết rằng đã chọn được một người có việc làm, xác suất để người này là nữ là \(\frac{7}{{30}}\).
a) Radar không thể phát hiện UAV khi UAV ở vị trí \(A\).
b) Phương trình tham số của đường bay của \(UAV\) là \(\left\{ \begin{array}{l}x = 300 - 3t\\y = - 400 + 4t\\z = 0\end{array} \right.,\,\,t \in \mathbb{R}\).
c) Trong suốt quá trình bay, sẽ có thời điểm UAV gây nhiễu được radar.
d) Radar có thể theo dõi UAV trong khoảng thời gian \(30\) phút.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Lát cắt của một vùng đất được mô hình hóa bởi hàm bậc ba \[y = f\left( x \right)\]có đồ thị như hình vẽ dưới (đơn vị trên các trục là km). Biết khoảng cách \[OM = 2\,{\rm{km}}\]; độ rộng của núi \[MN = 3,5\,{\rm{km}}{\rm{.}}\] Độ sâu của hồ nước là 450 m. Chiều cao của ngọn núi là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều cạnh \[a,\] cạnh bên \[SA\] vuông góc với mặt đáy, \(SA = \frac{{a\sqrt 6 }}{2}.\) Biết khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {SBC} \right)\] là \[ma\] (với \[m\] là số thực dương). Khi đó giá trị của \[m\] bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
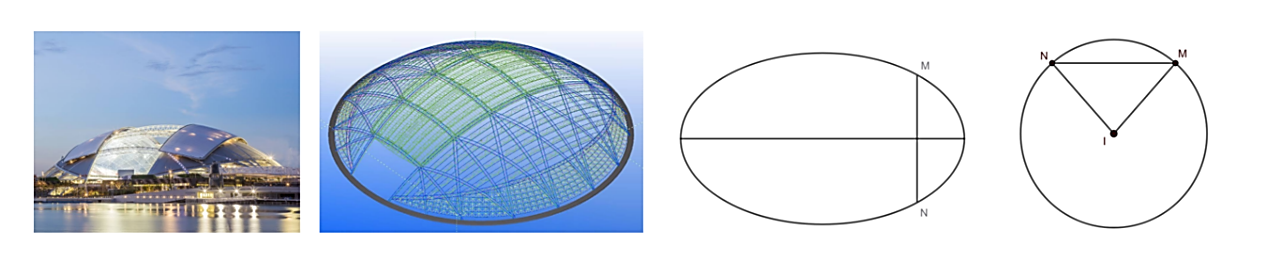
Sân vận động Sport Hub (Singapore) là sân có mái vòng kì vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm 2015. Nền sân là một elip \[\left( E \right)\] có trục lớn dài 150 m, trục bé dài 90 m. Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớp của \[\left( E \right)\] và cắt elip tại M, N thì ta được thiết diện luôn là một phần của hình tròn có tâm I (phần tô đậm) với MN là một dây cung và góc \[\widehat {MIN} = 90^\circ \]. Để lắp máy điều hòa không khí thì các kĩ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Biết rằng cách tính công suất cần đủ là 200 BTU/\[{{\rm{m}}^{\rm{3}}}\]. Hỏi cần ít nhất bao nhiêu chiếc điều hòa công suất 50 000 BTU?
Vào ngày 01/02/2023, ông An vay ngân hàng 200 triệu đồng với lãi suất 8%/năm. Ông dùng toàn bộ số tiền vay mua cổ phiếu mã SP với giá 50 nghìn đồng/1 cổ phiếu. Đúng sau một năm, để trả nợ ngân hàng ông An bán toàn bộ cổ phiếu đó với giá mỗi cổ phiếu là 55,6 nghìn đồng. Số tiền còn lại của ông An sau khi đã trả nợ cho ngân hàng là bao nhiêu triệu đồng?
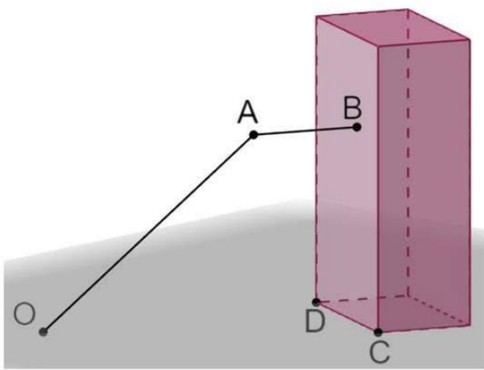
Một công ty logistics đang thử nghiệm hệ thống giao hàng tự động bằng máy bay không người lái (drone). Trong không gian \(Oxyz\), mỗi đơn vị trên các trục tương ứng với 1 mét trên thực tế. Mặt ngoài của một tòa nhà cao tầng được xem là một phần của mặt phẳng \(\left( P \right)\) thẳng đứng, đi qua hai điểm \(C\left( {10;50;0} \right)\) và \(D\left( {30;10;0} \right)\). Vị trí giao hàng là điểm \(B\) nằm trên mặt phẳng \(\left( P \right)\). Drone bắt đầu bay từ kho hàng tại gốc tọa độ \(O\left( {0;0;0} \right)\). Ban đầu, nó bay theo một đường thẳng đến vị trí \(A\left( {30;40;120} \right)\). Từ vị trí \(A\), drone thay đổi đường bay, di chuyển theo phương vuông góc với mặt phẳng \(\left( P \right)\) đến vị trí giao hàng \(B\). Tính khoảng cách từ \(O\) đến \(B\) (làm tròn kết quả đến hàng đơn vị).
Trong một đợt kiểm tra sức khỏe tại trường, có 200 học sinh được xét nghiệm một loại virus. Trong đó, biết rằng có 80 bạn thật sự bị nhiễm virus. Nếu một bạn bị nhiễm, thì xét nghiệm cho kết quả dương tính (tức là phát hiện đúng bệnh) với xác suất \(90\% \). Nếu một bạn không bị nhiễm, thì xét nghiệm vẫn có thể báo nhầm là dương tính (gọi là dương tính giả), với xác suất \(5\% \). Giả sử một bạn có kết quả xét nghiệm dương tính. Hỏi xác suất để bạn đó thật sự bị nhiễm virus là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?




