Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 24)
34 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Trong không gian \[Oxyz\], cho mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 9\]. Tọa độ tâm của mặt cầu \[\left( S \right)\] là
\[\left( {1; - 2; - 3} \right)\].
\[\left( {1;2; - 3} \right)\].
\[\left( {1; - 2;3} \right)\].
\[\left( {1;2;3} \right)\].
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = {x^2} - 4x\), trục hoành và hai đường thẳng \(x = 1\) và \(x = 3\). Khối tròn xoay được tạo thành khi quay hình phẳng \(\left( H \right)\) quanh trục \(Ox\) có thể tích là
\(V = \frac{{406}}{{15}}\).
\(V = \frac{{406}}{{15}}\pi \).
\(V = \frac{{22}}{3}\pi \).
\(V = \frac{{512}}{{15}}\pi \).
Cho cấp số nhân \[\left( {{u_n}} \right)\] có \[{u_1} = 1\] và \[{u_2} = 2\]. Số hạng \[{u_3}\] của cấp số nhân đó là
\[8\].
\[4\].
\[2\].
\[3\].
Mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) được cho trong bảng dưới đây.
Nhóm (đơn vị: triệu đồng) | \[\left[ {6;8} \right)\] | \[\left[ {8;10} \right)\] | \[\left[ {10;12} \right)\] | \[\left[ {12;14} \right)\] | \[\left[ {14;16} \right)\] |
|
Tần số | 6 | 14 | 18 | 10 | 2 | \[n = 50\] |
Tứ phân vị thứ nhất của mẫu số liệu đã cho (làm tròn đến hàng phần trăm) là
\[8,81\].
\[9,12\].
\[8,96\].
\[8,93\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây:
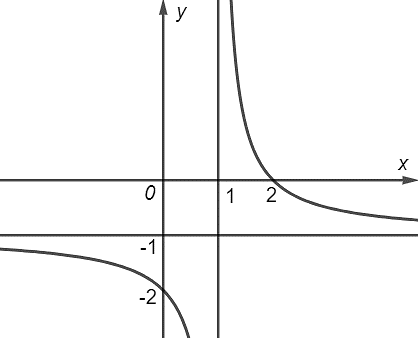
Đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng
\(x = 1\).
\(x = 0\).
\(x = - 1\).
\(y = - 1\).
Cho hình chóp \(S.ABCD\) có \[SA \bot \left( {ABCD} \right)\], \(ABCD\) là hình chữ nhật. Khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAD} \right)\) là độ dài đoạn thẳng nào dưới đây?
\(BD\).
\(AB\).
\(SA\).
\(AC\).
Cho hai biến cố \(A\) và \(B\) độc lập, \(P\left( A \right) = 0,4;\,P\left( B \right) = 0,3\). Khi đó \(P\left( {A \cap B} \right)\) bằng
\(0,3\).
\(0,7\).
\(0,12\).
\(0,4\).
Phương trình \({\log _2}\left( {x - 1} \right) = 2\) có nghiệm là
\(x = 4\).
\(x = 5\).
\(x = 2\).
\(x = 3\).
Trong không gian với hệ trục toạ độ \[Oxyz\], cho mặt phẳng \[\left( P \right):x + 2y - 3z + 1 = 0\]. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng \[\left( P \right)\]?
\[\overrightarrow {{n_1}} = \left( {1;2; - 3} \right)\].
\[\overrightarrow {{n_2}} = \left( {1;2;3} \right)\].
\[\overrightarrow {{n_3}} = \left( {1; - 2; - 3} \right)\].
\[\overrightarrow {{n_4}} = \left( {1; - 2;3} \right)\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\[\left( {0;1} \right)\].
\[\left( { - 1;0} \right)\].
\[\left( { - \infty ; - 1} \right)\].
\[\left( { - 1;1} \right)\].
Nguyên hàm của hàm số \[f\left( x \right) = \sin x\] là
\[\tan x + C\].
\[\cot x + C\].
\[\cos x + C\].
\[ - \cos x + C\].
Bất phương trình \[{3^{x + 1}} > 3\] có tập nghiệm là
\[\left( { - 1; + \infty } \right)\].
\[\left( {0; + \infty } \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( { - \infty ;1} \right)\].
a) Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
b) Hàm số \(f\left( x \right)\) có hai điểm cực trị.
c) Trên đoạn \(\left[ { - 2;2} \right]\), hàm số \(f\left( x \right)\) đạt giá trị lớn nhất bảng 2.
d) \(f\left( x \right) = {x^3} - 3x + 1\).
a) Nếu trời không mưa, khả năng An không đi xem đá bóng là \(30\% \).
b) Xác suất An đi xem đá bóng là 0,61.
c) Xác suất Bảo không đi xem đá bóng là 0,51.
d) Xác suất để ít nhất hai trong ba người bạn cùng đi xem trận bóng đá là 0,5612.
a) \(\int\limits_1^3 {3f\left( x \right)} \,{\rm{d}}x = 6\).
b) Nếu \(\int\limits_2^3 {f\left( x \right)} \,{\rm{d}}x = - 1\) thì \(\int\limits_1^2 {f\left( x \right)} \,{\rm{d}}x = 1\).
c) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {1;3} \right]\) thoả mãn \(F\left( 1 \right) = 3\) thì \(F\left( 3 \right) = 1\).
d) \(\int\limits_1^3 {\frac{{xf\left( x \right) + {x^2} - 1}}{x}} \,{\rm{d}}x = a + b\ln 3\;\,\left( {a \in \mathbb{R},b \in \mathbb{R}} \right)\). Ta có \(a + b = 5\).
a) \(\overrightarrow n = \left( {1; - 2; - 2} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).
b)\(A\left( {1; - 1;0} \right)\)là một điểm thuộc đường thẳng \(d\).
c) \(\cos \left( {d,\left( P \right)} \right) = \frac{{\sqrt 2 }}{3}\).
d)Phương trình mặt phẳng \(\left( Q \right)\) chứa đường thẳng \(d\) và vuông góc với \(\left( P \right)\) là
\(4x - 3y + 5z - 7 = 0\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được \(x\) mét vải lụa \(\left( {1 \le x \le 20} \right)\). Tổng chi phí sản xuất \(x\) mét vải lụa cho bởi hàm chi phí \(C\left( x \right) = \frac{{23}}{{36}}{x^3} + {x^2} + 200\) (tính bằng nghìn đồng). Giá của vải lụa tơ tằm là 300 nghìn đồng/mét và giả sử hộ luôn bán hết số sản phẩm làm ra trong một ngày. Để đạt lợi nhuận tối đa thì mỗi ngày hộ cần sản xuất bao nhiêu mét vải lụa?
Cho hình lăng trụ \[ABC.A'B'C'\] có đáy là tam giác đều cạnh \[2\,\,{\rm{dm}}\]. Hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( {ABC} \right)\] trùng với trọng tâm của tam giác \[ABC\]. Biết khoảng cách giữa hai đường \[AA'\] và \[BC\] bằng \[\frac{{\sqrt 3 }}{2}\,\,{\rm{dm}}\]. Tính thể tích \[V\left( {{\rm{d}}{{\rm{m}}^3}} \right)\] của khối lăng trụ \[ABC.A'B'C'\] (kết quả làm tròn đến hàng phần trăm).
Trong năm tới, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa: điều hòa hai chiều và điều hòa một chiều với số vốn ban đầu không vượt quá \(1,2\)tỉ đồng.
Biết rằng, giá mua vào và lợi nhuận dự kiến được cho bởi bảng sau:
| Điều hòa hai chiều | Điều hòa một chiều |
Giá mua vào | 20 triệu đồng/1 máy | 10 triệu đồng/1 máy |
Lợi nhuận dự kiến | 3,5 triệu đồng/1 máy | 2 triệu đồng/1 máy |
Cửa hàng ước tính rằng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Cửa hàng cần đầu tư kinh doanh \(x\) loại máy hai chiều và \(y\) loại máy một chiều thì lợi nhuận thu được là lớn nhất. Tổng \({x^2} + {y^2}\) bằng bao nhiêu?
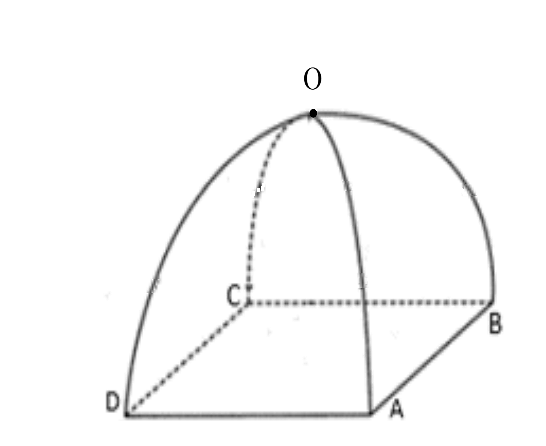
Một lều cắm trại có dạng như hình vẽ dưới, khung lều được tạo thành từ hai parabol giống nhau có chung đỉnh \[O\] và thuộc hai mặt phẳng vuông góc nhau (một parabol đi qua \[A,O,C\] và một parabol đi qua \[B,D,O\]), bốn chân tạo thành hình vuông \[ABCD\] có cạnh là \(2\sqrt 2 {\rm{ (m),}}\) chiều cao tính từ đỉnh lều là \(2{\rm{ (m)}}{\rm{.}}\) Biết mặt cắt của lều khi cắt bởi một mặt phẳng song song với mặt phẳng \(\left( {ABCD} \right)\) luôn là một hình vuông. Tính thể tích của lều (đơn vị là \({{\rm{m}}^3}\)).
Trạm kiểm soát không quân đang theo dõi hai máy bay chiến đấu Su-30 và MiG-31. Giả sử trong không gian với hệ trục tọa độ \[Oxyz,\] đơn vị đo mỗi trục là \[1\,\,{\rm{km}}\] và xem mặt phẳng \(\left( {Oxy} \right)\) là mặt đất, tại cùng một thời điểm theo dõi ban đầu: máy bay chiến đấu Su-30 ở tọa độ \(A\left( {0\,;35\,;10} \right)\) bay theo hướng vectơ \({\vec v_1} = \left( {3\,;4\,;0} \right)\) với tốc độ không đổi \[900{\rm{ (km/h)}}\] và máy bay chiến đấu MiG-31 ở tọa độ \[B\left( {31;10;11} \right),\] bay theo hướng \[{\vec v_2} = \left( {5\,;12\,;0} \right)\] với tốc độ không đổi \[910{\rm{ (km/h)}}\]. Khu vực này có gió mạnh thổi với vận tốc \(80{\rm{ (km/h)}}\) theo hướng vectơ \(\vec u = \left( { - 3\,;0\,;4} \right),\) gió ảnh hưởng đến cả hai máy bay trong quá trình bay. Một khu vực không phận bị hạn chế bay đã được một quốc gia khác thiết lập, có dạng hình trụ với tâm đáy tại \(C\left( {178\,;430\,;0} \right)\), bán kính đáy \[7\,{\rm{km,}}\] trục vuông góc với mặt đất và chiều cao \[43\,{\rm{km,}}\] máy bay MiG-31 có nhiệm vụ bay vào khu vực không phận bị hạn chế để thăm dò. Tại thời điểm máy bay chiến đấu MiG-31 bay ra khỏi khu vực không phận bị hạn chế thì khoảng cách của 2 máy bay chiến đấu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần chục).

Một thành phố có ba loại phương tiện giao thông công cộng: xe buýt, tàu điện ngầm và taxi. Tỉ lệ sử dụng mỗi loại phương tiện đối với xe buýt \(40\% \), tàu điện ngầm \(35\% \), taxi \(25\% \). Tỉ lệ trễ giờ của xe buýt, tàu điện ngầm và taxi trong một tháng lần lượt là: \(20\% \), \(10\% \), \(5\% \). Anh Lộc là một người dân trong thành phố. Trong tháng đầu tiên, anh Lộc chọn một trong ba loại phương tiện trên để đi làm, sao cho xác suất chọn mỗi loại phương tiện đúng bằng tỉ lệ sử dụng phương tiện đó của người dân trong thành phố. Từ tháng thứ hai trở đi, cách anh Lộc chọn phương tiện đi làm phụ thuộc vào việc anh có bị trễ giờ trong tháng trước hay không: Nếu tháng trước anh Lộc không bị trễ giờ: Anh ấy tiếp tục sử dụng loại phương tiện mà anh đã đi trong tháng đó. Nếu tháng trước anh Lộc bị trễ giờ: Anh ấy sẽ chọn ngẫu nhiên một trong hai loại phương tiện còn lại để đi làm trong tháng tiếp theo, với xác suất chọn mỗi loại là \(50\% \). Xác suất để anh Lộc sử dụng taxi trong tháng thứ ba có dạng \(\frac{a}{b}\) (là phân số tối giản). Tính \(b - 2a\)?




