12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh \(a\). Giá trị của \(\overrightarrow {AC'} \cdot \overrightarrow {B'D'} \) là:
\(0\).
\( - \frac{1}{2}{a^2}\).
\(\sqrt 6 {a^2}\).
\( - \frac{{\sqrt 2 }}{2}{a^2}\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sin x;y = \cos x\) và các đường thẳng \(x = 0\), \(x = 7\) được tính bằng công thức:
\(S = \int\limits_0^7 {\left( { - \sin x + \cos x} \right){\rm{d}}x} \).
\(S = \int\limits_0^7 {\left| {\sin x - \cos x} \right|{\rm{d}}x} \).
\(S = \int\limits_0^7 {\left( {\sin x - \cos x} \right){\rm{d}}x} \).
\(S = \int\limits_0^7 {\left( {\sin x + \cos x} \right){\rm{d}}x} \).
Khảo sát thời gian tự học của một số học sinh lớp 11 trong một ngày, người ta thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;30} \right)\) |
\(\left[ {30;60} \right)\) |
\(\left[ {60;90} \right)\) |
\(\left[ {90;120} \right)\) |
\(\left[ {120;150} \right)\) |
|
Số học sinh |
\(8\) |
\(14\) |
\(11\) |
\(9\) |
\(3\) |
Nhóm chứa trung vị của mẫu số liệu trên là
\(\left[ {60;90} \right)\).
\(\left[ {0;30} \right)\).
\(\left[ {30;60} \right)\).
\(\left[ {90;120} \right)\).
Trong không gian \(\left( {Oxyz} \right)\), mặt phẳng \(\left( {Oyz} \right)\) có một vectơ pháp tuyến là
\(\overrightarrow n = \left( {1;1;1} \right)\).
\(\overrightarrow n = \left( {0;0;0} \right)\).
\(\overrightarrow n = \left( {0;1;1} \right)\).
\(\overrightarrow n = \left( {1;0;0} \right)\).
Đồ thị hàm số \[y = - x + 2 + \frac{1}{x}\] có đường tiệm cận xiên là:
\[y = - x + 2\].
\[y = - \frac{1}{x}\].
\(y = x - 2\).
\(y = \frac{1}{x}\).
Tập nghiệm của bất phương trình \[{e^x} > 1\] là:
\[\left( {1\,; + \infty } \right)\].
\[\left( { - \infty \,;0} \right)\].
\[\left( { - \infty ; + \infty } \right)\].
\(\left( {0; + \infty } \right)\).
Tập nghiệm của phương trình \[{\log _4}x = 0\] là:
\[x = - 1\].
\[x = 1\].
\[x = 0\].
\(x = 4\).
Trong không gian với hệ tọa độ \[Oxyz\], phương trình của đường thẳng đi qua hai điểm \[E\left( { - 1;4;2} \right)\]và \[F\left( { - 5\,;0\,;3} \right)\]là:
\[\frac{{x + 1}}{{ - 4}} = \frac{{y - 4}}{{ - 4}} = \frac{{z - 2}}{1}\].
\[\frac{{x + 4}}{{ - 1}} = \frac{{y + 4}}{4} = \frac{{z - 1}}{2}\].
\[\frac{{x - 4}}{{ - 1}} = \frac{{y - 4}}{4} = \frac{{z + 1}}{2}\].
\[\frac{{x - 1}}{{ - 4}} = \frac{{y + 4}}{{ - 4}} = \frac{{z + 2}}{1}\].
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = {\rm{cos}}x + 1\) là:
\({\rm{sin}}x + C\).
\( - {\rm{sin}}x + x + C\).
\({\rm{cos}}x + x + C\).
\({\rm{sin}}x + x + C\).
Cho cấp số cộng \[\left( {{u_n}} \right)\]có \[{u_1} = 1\] và \[{u_2} = - 3\]. Số hạng \[{u_4}\] của cấp số cộng đã cho là
\[ - 11\].
\[ - 27\].
\[ - 7\].
\[ - 14\].
Cho hàm số \[y = {x^3} - 3{x^2} - 2025\]. Hàm số đã cho nghịch biến trên khoảng:
\[\left( {0;2} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( { - \infty ; + \infty } \right)\].
\[\left( {2; + \infty } \right)\].
Cho tứ diện \[S.ABC\]có các cạnh \[SA,\,SB,\,SC\]đôi một vuông góc và \[SA = SB = SC = 1\] (minh họa như hình dưới). Gọi \[\alpha \]là góc phẳng nhị diện \[\left[ {S,BC,A} \right]\]. Tính \[\cos \alpha \].
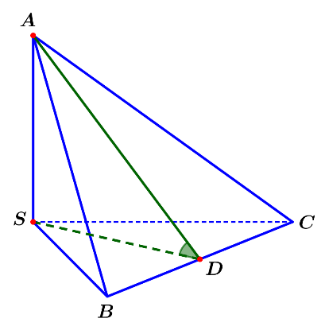
\[\frac{2}{5}\].
\[\frac{{\sqrt 3 }}{3}\].
\[\frac{1}{3}\].
\[\frac{{2\sqrt 5 }}{5}\].
