12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho cấp số nhân \[\left( {{u_n}} \right)\]với \[{u_1} = 3\] và công bội \[q = - 2\]. Giá trị của \[{u_4}\] bằng
\(24\).
\( - 12\).
\( - 24\).
\(12\).
Cho hàm số\[y = f\left( x \right)\] xác định trên \[\mathbb{R}\]và có bảng biến thiên như sau:
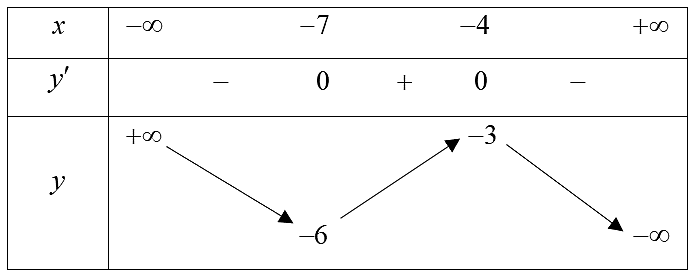
Điểm cực đại của hàm số \[y = f\left( x \right)\] là
\[x = - 7\].
\[x = - 6\].
\[x = - 3\].
\[x = - 4\].
Nguyên hàm \[F\left( x \right)\] của hàm số \[f\left( x \right) = \frac{1}{x} + e\] là
\[F\left( x \right) = - \frac{1}{{{x^2}}} + {e^x} + C\].
\[F\left( x \right) = \ln \left| x \right| + ex + C\].
\[F\left( x \right) = \ln \left| x \right| + {e^x} + C\].
\[F\left( x \right) = \ln x + e + C\].
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):2x + y - 1 = 0\) có một vectơ pháp tuyến là
\({\vec n_1} = \left( { - 2; - 1;1} \right)\).
\({\vec n_2} = \left( {2;1; - 1} \right)\).
\({\vec n_3} = \left( {1;2;0} \right)\).
\({\vec n_4} = \left( {2;1;0} \right)\).
Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau:
|
Lượng nước tiêu thụ (m3) |
\(\left[ {3\,;\,6} \right)\) |
\(\left[ {6\,;\,9} \right)\) |
\(\left[ {9\,;\,12} \right)\) |
\(\left[ {12\,;\,15} \right)\) |
\(\left[ {15\,;\,18} \right)\) |
|
Số hộ gia đình |
\(20\) |
\(60\) |
\(40\) |
\(32\) |
\(7\) |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
\[20\,\,{{\rm{m}}^{\rm{3}}}\].
\[18\,\,{{\rm{m}}^{\rm{3}}}\].
\[3\,\,{{\rm{m}}^{\rm{3}}}\].
\[15\,\,{{\rm{m}}^{\rm{3}}}\].
Cho hàm số \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\]. Biết \[F\left( 1 \right) = - 3,F\left( { - 2} \right) = 12\]. Tính \[I = \int\limits_{ - 2}^1 {f\left( x \right)} \,{\rm{d}}x\].
\[I = 9\].
\[I = 15\].
\[I = - 36\].
\[I = - 15\].
Cho hai biến cố độc lập \[A\] và \[B\]với \[P\left( A \right) = 0,7;\,P\left( B \right) = 0,2\]. Khi đó, \[P\left( {A|B} \right)\]bằng:
\(0,3\).
\[0,7\].
\(0,8\).
\(0,2\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {1;5} \right]\) và có đồ thị như hình vẽ sau:
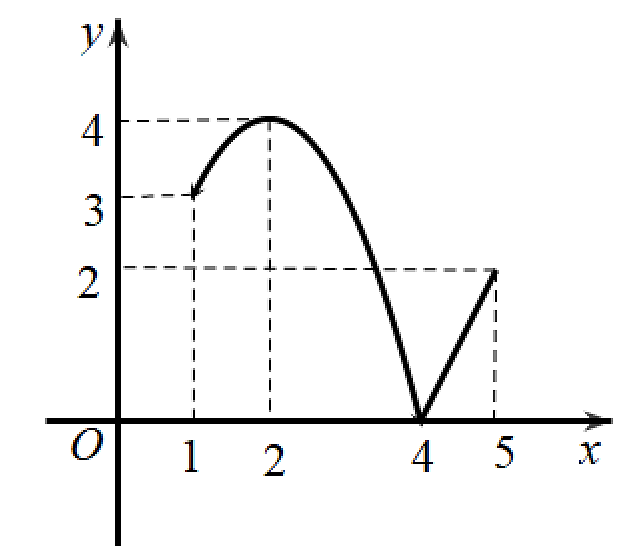
Trên đoạn \(\left[ {1;5} \right]\), hàm số đã cho đạt giá trị lớn nhất tại điểm
\(x = 4\).
\(x = 1\).
\(x = 2\).
\(x = 5\).
Tập nghiệm của bất phương trình \({\rm{lo}}{{\rm{g}}_{\frac{1}{2}}}\left( {x + 1} \right) > - 1\) là
\(\left( { - 1;1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( {0;3} \right)\).
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - 2x - 1}}{{x - 2}}\) là
\(y = - 2\).
\(y = 2\).
\(x = 2\).
\(x = - 2\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Cạnh \(SA\) vuông góc với mặt phẳng đáy và có độ dài là \(2a\). Thể tích khối chóp \(S.BCD\) bằng
\(\frac{{{a^3}}}{8}\).
\(\frac{{{a^3}}}{3}\).
\(\frac{{{a^3}}}{4}\).
\(\frac{{2{a^3}}}{3}\).
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) có phương trình \({x^2} + {y^2} + {z^2} = \frac{1}{4}\). Bán kính \(R\) của mặt cầu \(\left( S \right)\) bằng
\(R = \frac{1}{2}\).
\(R = \frac{1}{4}\).
\(R = 2\).
\(R = 4\).
