12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Trọng lượng của 20 củ sâm trong một lô củ sâm được thu hoạch sau sáu năm trồng tại một cơ sở trồng sâm có bảng tần số ghép nhóm sau (đơn vị: gam):
|
Nhóm |
\(\left[ {40;45} \right)\) |
\(\left[ {45;50} \right)\) |
\(\left[ {50;55} \right)\) |
\(\left[ {55;60} \right)\) |
|
Tần số |
\(3\) |
\(7\) |
\(8\) |
\(2\) |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:
\(3,3\).
\(9,5\).
\(6,7\).
\(8,6\).
Tập nghiệm của bất phương trình \({3^{x - 2}} > 9\) là:
\(\left( { - \infty ;2} \right)\).
\(\left( {4; + \infty } \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( {5; + \infty } \right)\).
Trong không gian \(Oxyz\), cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 - 2t}\\{y = 3 + t}\\{z = - 1 + 4t}\end{array}} \right.\). Điểm nào dưới đây thuộc đường thẳng \(d\)?
\(P\left( { - 1; - 3;1} \right)\).
\(M\left( {1;3; - 1} \right)\).
\(N\left( { - 2;2;4} \right)\).
\(Q\left( { - 1;1;2} \right)\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết hàm số \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) và \(F\left( 3 \right) = 5,F\left( 1 \right) = 1\). Tích phân \(\int\limits_1^3 {f\left( x \right){\rm{d}}x} \) bằng:
\( - 4\).
\(5\).
\(6\).
\(4\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong như hình vẽ dưới đây.
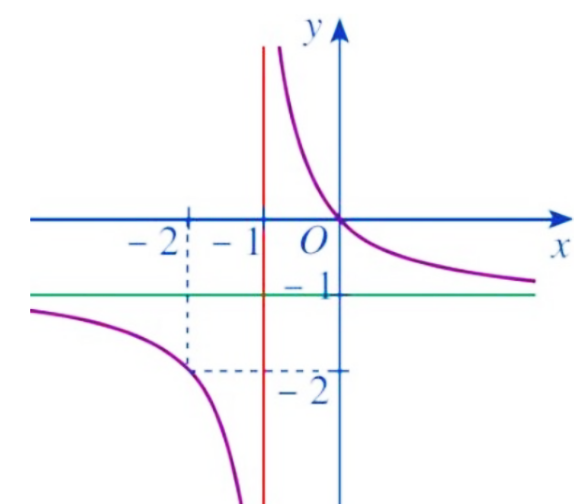
Hàm số nghịch biến trên khoảng (các khoảng) nào sau đây?
\(\left( { - 2;0} \right)\).
\(\left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
\(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
Nghiệm của phương trình\({\log _2}x = 3\) là
\(x = \frac{3}{2}\).
\(x = 8\).
\(x = 6\).
\(x = 5\).
Cho cấp số cộng \(\left( {{u_n}} \right)\)có \({u_1} = - 3,{u_6} = 27\). Công sai \(d\) của cấp số cộng đã cho là:
\[d = 8\].
\[d = 5\].
\[d = 7\].
\[d = 6\].
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\sqrt 2 \). Tam giác \(ABC\) vuông cân tại \(B\) và \(AB = a\). Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng
\(60^\circ \).
\(30^\circ \).
\(45^\circ \).
\(90^\circ \).
Cho đồ thị hàm số như hình dưới đây.
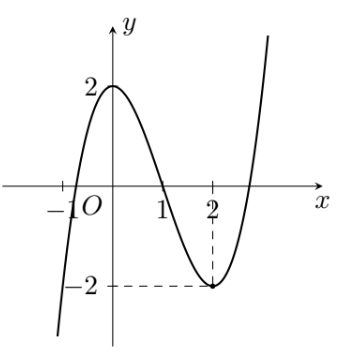
Hàm số đó là hàm số nào?
\(y = \frac{{x + 1}}{{x + 2}}\).
\(y = - {x^3} - 6x + 2\).
\(y = - {x^3} + 3{x^2} + 2\).
\(y = {x^3} - 3{x^2} + 2\).
Trong không gian \(Oxyz\), mặt cầu \(\left( S \right)\) có phương trình \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 4\) có bán kính bằng
\(16\).
\(8\).
\(2\).
\(4\).
Khẳng định nào dưới đây đúng?
\(\int {{{2025}^x}{\rm{d}}x} = \frac{{{{2025}^{x + 1}}}}{{x + 1}} + C\).
\(\int {{{2025}^x}{\rm{d}}x} = \frac{{{{2025}^{x + 1}}}}{{\ln 2025}} + C\).
\(\int {{{2025}^x}{\rm{d}}x} = {2025^x} \cdot \ln 2025 + C\).
\(\int {{{2025}^x}{\rm{d}}x} = \frac{{{{2025}^x}}}{{\ln 2025}} + C\).
Cho hình chóp có diện tích mặt đáy là \(3{a^2}\) và chiều cao bằng \(6a\). Thể tích của khối chóp bằng:
\(18{a^3}\).
\(6{a^3}\).
\(9{a^3}\).
\(3{a^3}\).
