12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) là hàm đa thức có đạo hàm \(f'\left( x \right) = x\left( {{x^2} - 1} \right){\left( {x - 2} \right)^2}\). Số điểm cực tiểu của đồ thị hàm số là:
\[1\].
\[4\].
\[3\].
\[2\].
Với \(a,b\) là các số thực dương tùy ý, gọi \(x = {\log _2}a,y = {\log _2}b,P = {\log _2}\left( {{a^2}{b^3}} \right)\). Khẳng định nào sau đây là đúng?
\(P = {x^2}{y^3}\).
\(P = {x^2} + {y^3}\).
\(P = 2x + 3y\).
\(P = 6xy\).
Các nghiệm của phương trình \[\cos 2x = 0\] là
\(x = \frac{\pi }{2} + k\pi \,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{8} + \frac{{k\pi }}{2}\,\left( {k \in \mathbb{Z}} \right)\).
\(x = k\frac{\pi }{2}\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k\frac{\pi }{2}\,\left( {k \in \mathbb{Z}} \right)\).
Trong không gian \[Oxyz\], cho đường thẳng \(d:\frac{{x - 3}}{2} = \frac{{y - 4}}{{ - 5}} = \frac{{z + 5}}{3}\). Điểm nào sau đây thuộc đường thẳng \(d\)?
\[M\left( {3;4; - 5} \right)\].
\[N\left( {2; - 5;3} \right)\].
\[P\left( { - 3; - 4;5} \right)\].
\[Q\left( {2;5; - 3} \right)\].
Tập nghiệm của bất phương trình \({\left( {\frac{3}{4}} \right)^{2x - 1}} \le {\left( {\frac{4}{3}} \right)^{ - 2 + x}}\) là:
\(S = \left( { - \infty ;1} \right]\).
\(S = \left( {1; + \infty } \right)\).
\(S = \left[ {1; + \infty } \right)\).
\(S = \left( { - \infty ;1} \right)\).
Bảng sau đây biểu diễn mẫu số liệu ghép nhóm thống kê về nhu cầu mức giá mua nhà (đơn vị triệu đồng\({\rm{/}}{{\rm{m}}^{\rm{2}}}\)) của khách hàng tại một công ty xây dựng:
|
Nhóm |
\(\left[ {10;14} \right)\) |
\(\left[ {14;18} \right)\) |
\(\left[ {18;22} \right)\) |
\(\left[ {22;26} \right)\) |
\(\left[ {26;30} \right)\) |
|
Tần số |
\[54\] |
\(78\) |
\(120\) |
\(45\) |
\(12\) |
Khoảng biến thiên của một số liệu ghép nhóm trên là:
\(9\).
\(4\).
\(20\).
\(108\).
Công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và 2 đường thẳng \(x = a,x = b\left( {a < b} \right)\), xung quanh trục \(Ox\) là:
\(V = \int\limits_a^b {{f^2}\left( x \right){\rm{d}}x} \).
\(V = \pi \int\limits_a^b {f\left( x \right){\rm{d}}x} \).
\(V = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \).
\(V = \pi \int\limits_a^b {{f^2}\left( x \right){\rm{d}}x} \).
Chohàm số có đồ thị như hình vẽ dưới đây.
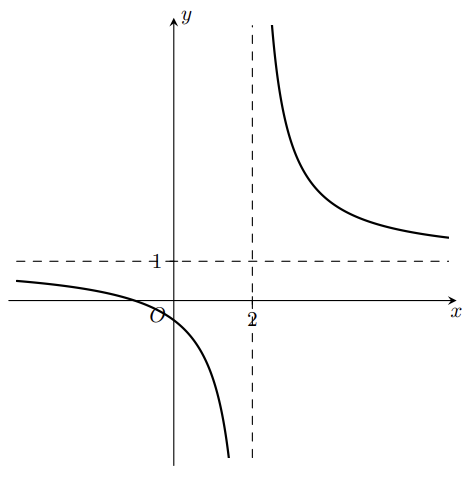
Đồ thị hàm số có tiệm cận ngang là:
\(y = 1\).
\(y = 2\).
\(x = 1\).
\(x = 2\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Góc giữa hai đường thẳng nào sau đây bằng \(90^\circ \)?
\(SA,SB\).
\(SB,AD\).
\(SA,BD\).
\(SA,SC\).
Trong không gian \[Oxyz\], mặt phẳng nào dưới đây nhận vectơ \(\overrightarrow n = \left( {3;1; - 7} \right)\) làm một vectơ pháp tuyến?
\(3x - y - 7z + 1 = 0\).
\(3x + z + 7 = 0\).
\(3x + y - 7z - 3 = 0\).
\(3x + y - 7 = 0\).
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Mệnh đề nào sau đây đúng?
\(\left| {\overrightarrow {BA} + \overrightarrow {B{B_1}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {B{D_1}} } \right|\).
\(\left| {\overrightarrow {A{A_1}} + \overrightarrow {{C_1}D} + \overrightarrow {{C_1}{D_1}} } \right| = 0\).
\(\left| {\overrightarrow {A{B_1}} - \overrightarrow {A{D_1}} } \right| = \left| {\overrightarrow {B{D_1}} } \right|\).
\(\left| {\overrightarrow {A{B_1}} + \overrightarrow {A{D_1}} } \right| = \left| {\overrightarrow {A{C_1}} } \right|\).
Biết \(\int\limits_1^3 {f\left( x \right){\rm{d}}x = 5} \) và \(\int\limits_1^3 {g\left( x \right){\rm{d}}x = - 7} \). Giá trị của \(\int\limits_1^3 {\left[ {3f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} \) bằng
\( - 31\).
\(29\).
\(1\).
\( - 29\).
