12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Trong không gian \[Oxyz\], cho mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 9\]. Tọa độ tâm của mặt cầu \[\left( S \right)\] là
\[\left( {1; - 2; - 3} \right)\].
\[\left( {1;2; - 3} \right)\].
\[\left( {1; - 2;3} \right)\].
\[\left( {1;2;3} \right)\].
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = {x^2} - 4x\), trục hoành và hai đường thẳng \(x = 1\) và \(x = 3\). Khối tròn xoay được tạo thành khi quay hình phẳng \(\left( H \right)\) quanh trục \(Ox\) có thể tích là
\(V = \frac{{406}}{{15}}\).
\(V = \frac{{406}}{{15}}\pi \).
\(V = \frac{{22}}{3}\pi \).
\(V = \frac{{512}}{{15}}\pi \).
Cho cấp số nhân \[\left( {{u_n}} \right)\] có \[{u_1} = 1\] và \[{u_2} = 2\]. Số hạng \[{u_3}\] của cấp số nhân đó là
\[8\].
\[4\].
\[2\].
\[3\].
Mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) được cho trong bảng dưới đây.
|
Nhóm (đơn vị: triệu đồng) |
\[\left[ {6;8} \right)\] |
\[\left[ {8;10} \right)\] |
\[\left[ {10;12} \right)\] |
\[\left[ {12;14} \right)\] |
\[\left[ {14;16} \right)\] |
|
|
Tần số |
6 |
14 |
18 |
10 |
2 |
\[n = 50\] |
Tứ phân vị thứ nhất của mẫu số liệu đã cho (làm tròn đến hàng phần trăm) là
\[8,81\].
\[9,12\].
\[8,96\].
\[8,93\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây:
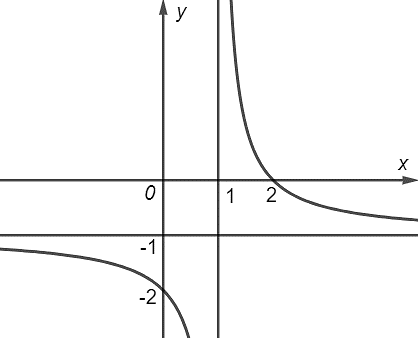
Đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng
\(x = 1\).
\(x = 0\).
\(x = - 1\).
\(y = - 1\).
Cho hình chóp \(S.ABCD\) có \[SA \bot \left( {ABCD} \right)\], \(ABCD\) là hình chữ nhật. Khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAD} \right)\) là độ dài đoạn thẳng nào dưới đây?
\(BD\).
\(AB\).
\(SA\).
\(AC\).
Cho hai biến cố \(A\) và \(B\) độc lập, \(P\left( A \right) = 0,4;\,P\left( B \right) = 0,3\). Khi đó \(P\left( {A \cap B} \right)\) bằng
\(0,3\).
\(0,7\).
\(0,12\).
\(0,4\).
Phương trình \({\log _2}\left( {x - 1} \right) = 2\) có nghiệm là
\(x = 4\).
\(x = 5\).
\(x = 2\).
\(x = 3\).
Trong không gian với hệ trục toạ độ \[Oxyz\], cho mặt phẳng \[\left( P \right):x + 2y - 3z + 1 = 0\]. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng \[\left( P \right)\]?
\[\overrightarrow {{n_1}} = \left( {1;2; - 3} \right)\].
\[\overrightarrow {{n_2}} = \left( {1;2;3} \right)\].
\[\overrightarrow {{n_3}} = \left( {1; - 2; - 3} \right)\].
\[\overrightarrow {{n_4}} = \left( {1; - 2;3} \right)\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\[\left( {0;1} \right)\].
\[\left( { - 1;0} \right)\].
\[\left( { - \infty ; - 1} \right)\].
\[\left( { - 1;1} \right)\].
Nguyên hàm của hàm số \[f\left( x \right) = \sin x\] là
\[\tan x + C\].
\[\cot x + C\].
\[\cos x + C\].
\[ - \cos x + C\].
Bất phương trình \[{3^{x + 1}} > 3\] có tập nghiệm là
\[\left( { - 1; + \infty } \right)\].
\[\left( {0; + \infty } \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( { - \infty ;1} \right)\].
