Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 3)
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho hàm số ![]() liên tục và có bảng biến thiên trên đoạn
liên tục và có bảng biến thiên trên đoạn ![]() như hình vẽ bên. Khẳng định nào sau đây là đúng?
như hình vẽ bên. Khẳng định nào sau đây là đúng?
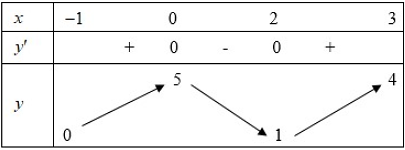
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Phương trình ![]() có nghiệm là:
có nghiệm là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có một nguyên hàm là
và có một nguyên hàm là ![]() . Biết rằng
. Biết rằng ![]() . Giá trị của biểu thức
. Giá trị của biểu thức 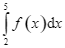 bằng:
bằng:
3.
–11.
7.
11.
Cho hình chóp ![]() có đáy
có đáy ![]() là tam giác vuông tại
là tam giác vuông tại ![]() với
với ![]() , cạnh
, cạnh ![]() vuông góc với
vuông góc với ![]() và
và ![]() . Tính thể tích khối chóp
. Tính thể tích khối chóp ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đồ thị hàm số ![]() có toạ độ điểm cực đại là
có toạ độ điểm cực đại là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() có đồ thị như hình vẽ dưới đây.
có đồ thị như hình vẽ dưới đây.
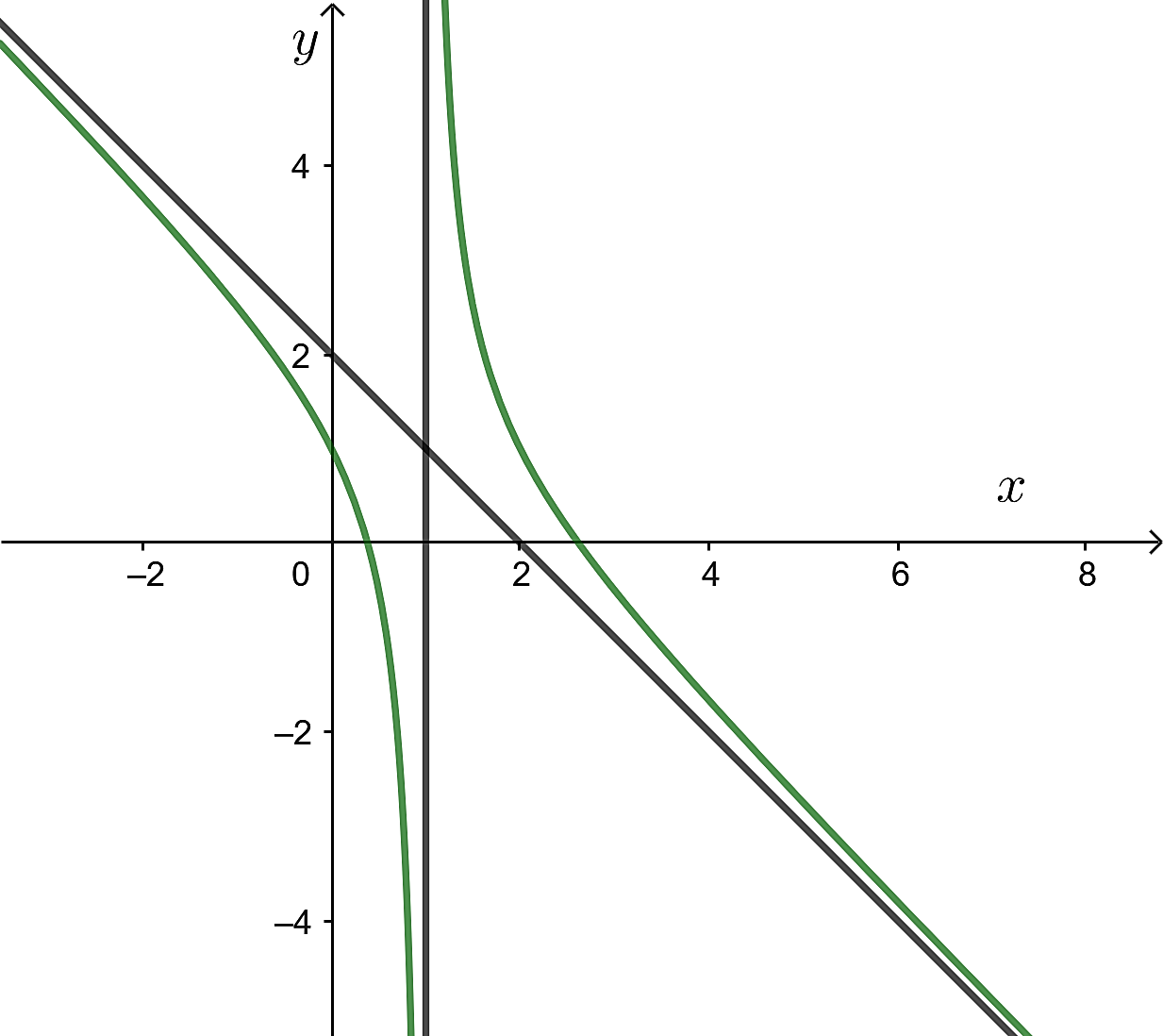
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Họ nguyên hàm của hàm số ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Một tổ có ![]() học sinh nữ và
học sinh nữ và ![]() học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học sinh của tổ đó đi trực nhật?
học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học sinh của tổ đó đi trực nhật?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho cấp số cộng ![]() . Xác định công sai
. Xác định công sai ![]() của cấp số cộng.
của cấp số cộng.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đồ thị sau đây là của hàm số nào?
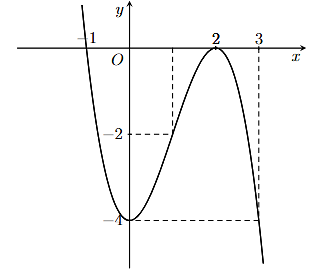
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tiệm cận ngang của đồ thị hàm số ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ tọa độ ![]() , phương trình của đường thẳng
, phương trình của đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Bác Lâm muốn gò một cái thùng bằng tôn dạng hình hộp chữ nhật không nắp có đáy là hình vuông và đựng đầy được 32 lít nước. Gọi độ dài cạnh đáy của thùng là ![]() , chiều cao của thùng là
, chiều cao của thùng là ![]() .
.
a) Thể tích của thùng là ![]() .
.
b) Tổng diện tích xung quanh và diện tích đáy của thùng là: ![]() .
.
c) Đạo hàm của hàm số ![]() là
là ![]() .
.
d) Để làm được cái thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là ![]()
Kết quả kiểm tra cân nặng của 20 học sinh nam lớp 12A (làm tròn kết quả đến hàng đơn vị của kilôgam) được cho bởi bảng dưới đây.
Nhóm | Giá trị đại diện | Tần số |
| 62 | 8 |
| 66 | 9 |
| 70 | 1 |
| 74 | 1 |
| 78 | 1 |
|
|
|
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đã cho là 20.
b) Số trung bình cộng của mẫu số liệu ghép nhóm đã cho được tính bằng công thức
![]() .
.
c) Phương sai của mẫu số liệu ghép nhóm đã cho là 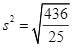 .
.
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến hàng phần mười của
kilôgam) là 4 kg.
Trong không gian tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng
![]() và
và ![]() .
.
a) Vectơ có tọa độ ![]() là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng ![]() .
.
b) Vectơ có toạ độ ![]() là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng ![]() .
.
c) Côsin của góc giữa hai vectơ ![]() và
và ![]() bằng
bằng ![]() .
.
d) Góc giữa hai mặt phẳng ![]() và
và ![]() bằng
bằng ![]() .
.
Hai chất điểm chuyển động ngược chiều nhau thì xảy ra va chạm, hai chất điểm tiếp tục di chuyển theo chiều ban đầu thêm một quãng đường nữa thì dừng hẳn. Biết rằng sau khi va chạm, một chất điểm di chuyển tiếp với vận tốc ![]()
![]() , chất điểm còn lại di chuyển với vận tốc
, chất điểm còn lại di chuyển với vận tốc ![]()
![]() .
.
a) Quãng đường chất điểm thứ nhất di chuyển sau khi va chạm được biểu diễn bởi hàm số![]() .
.
b) Quãng đường chất điểm thứ hai di chuyển sau khi va chạm được biểu diễn bởi hàm số![]() .
.
c) Quãng đường chất điểm thứ nhất di chuyển sau khi va chạm là ![]() .
.
d) Khoảng cách hai chất điểm khi đã dừng hẳn ![]() .
.
PHẦN III. Câu trắc nghiệm trả lời ngắn Giả sử ![]() với
với ![]() là các hằng số dương. Giá trị của biểu thức
là các hằng số dương. Giá trị của biểu thức ![]() bằng bao nhiêu?
bằng bao nhiêu?
Trong một khung lưới ô vuông gồm các hình lập phương, người ta đưa ra một cách kiểm tra bốn nút lưới (đỉnh hình lập phương) bất kì có đồng phẳng hay không bằng cách gắn hệ trục toạ độ ![]() vào khung lưới ô vuông và lập phương trình mặt phẳng đi qua ba nút lưới trong bốn nút lưới đã cho. Giả sử có ba nút lưới mà toạ độ lần lượt là
vào khung lưới ô vuông và lập phương trình mặt phẳng đi qua ba nút lưới trong bốn nút lưới đã cho. Giả sử có ba nút lưới mà toạ độ lần lượt là ![]() ,
, ![]() ,
,![]() và mặt phẳng đi qua ba nút lưới đó có phương trình
và mặt phẳng đi qua ba nút lưới đó có phương trình ![]() . Giá trị của
. Giá trị của ![]() là bao nhiêu?
là bao nhiêu?
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ ![]() là
là ![]() Nếu coi
Nếu coi ![]() là hàm số xác định trên đoạn
là hàm số xác định trên đoạn ![]() thì đạo hàm
thì đạo hàm ![]() được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm
được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm ![]() . Giả sử khoảng thời gian mà tốc độ truyền bệnh giảm là từ ngày thứ
. Giả sử khoảng thời gian mà tốc độ truyền bệnh giảm là từ ngày thứ ![]() đến ngày thứ
đến ngày thứ ![]() . Khi đó
. Khi đó ![]() bằng bao nhiêu?
bằng bao nhiêu?
Để nghiên cứu xác suất của một loại cây trồng mới phát triển bình thường, người ta trồng hạt giống của loại cây đó trên hai ô đất thí nghiệm ![]() ,
, ![]() khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất
khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các ô đất ![]() ,
, ![]() lần lượt là
lần lượt là ![]() và
và ![]() . Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xác suất của biến cố hạt giống chỉ phát triển bình thường trên một ô đất là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xác suất của biến cố hạt giống chỉ phát triển bình thường trên một ô đất là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Ông An đang ở trong rừng để đào vàng. Ông ta tìm thấy vàng ở điểm ![]() , cách điểm
, cách điểm ![]()
![]() Điểm
Điểm ![]() nằm trên đường bờ biển (đường bờ biển là đường thẳng). Trại của Ông An nằm ở
nằm trên đường bờ biển (đường bờ biển là đường thẳng). Trại của Ông An nằm ở ![]() , cách điểm
, cách điểm ![]()
![]() Điểm
Điểm ![]() cũng thuộc đường bờ biển. Biết rằng
cũng thuộc đường bờ biển. Biết rằng ![]() ,
,![]() và
và ![]() (Như hình vẽ)
(Như hình vẽ)
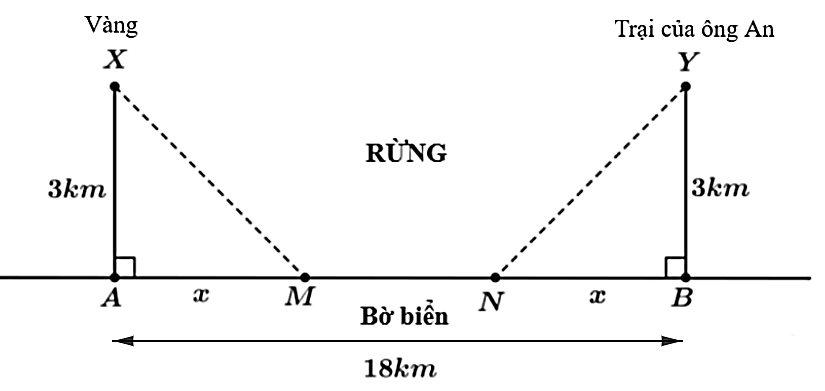
Khi đang đào vàng, ông An bị rắn cắn, chất độc lan vào máu. Sau khi bị cắn, nồng độ chất độc trong máu tăng theo thời gian được tính theo hàm số ![]() (mg/l), trong đó
(mg/l), trong đó ![]() là nồng độ,
là nồng độ, ![]() là thời gian tính bằng giờ sau khi bị rắn cắn. Ông An cần quay trở lại trại để lấy thuốc giải độc. Ông ấy chạy trong rừng với vận tốc
là thời gian tính bằng giờ sau khi bị rắn cắn. Ông An cần quay trở lại trại để lấy thuốc giải độc. Ông ấy chạy trong rừng với vận tốc ![]() và chạy trên đường bờ biển với vận tốc
và chạy trên đường bờ biển với vận tốc ![]() Để về đến trại ông An cần chạy từ trong rừng qua điểm
Để về đến trại ông An cần chạy từ trong rừng qua điểm ![]() trên đường bờ biển. Chọn điểm
trên đường bờ biển. Chọn điểm ![]() trên đường bờ biển sao cho khi ông An về đến trại nồng độ chất độc trong máu thấp nhất. Tính nồng độ chất độc trong máu thấp nhất khi ông An về đến trại (làm tròn đáp án đến hàng phần chục).
trên đường bờ biển sao cho khi ông An về đến trại nồng độ chất độc trong máu thấp nhất. Tính nồng độ chất độc trong máu thấp nhất khi ông An về đến trại (làm tròn đáp án đến hàng phần chục).
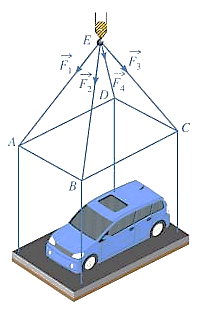
Một chiếc ô tô được đặt trên mặt đáy dưới một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình vuông ![]() , mặt phẳng
, mặt phẳng ![]() song song với mặt mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc
song song với mặt mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc ![]() của chiến cần cẩu sao cho các đoạn dây cáp
của chiến cần cẩu sao cho các đoạn dây cáp ![]() có độ dài bằng nhau và cùng tạo với mặt phẳng
có độ dài bằng nhau và cùng tạo với mặt phẳng ![]() một góc
một góc ![]() như hình vẽ. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết lực căng
như hình vẽ. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết lực căng ![]() , trọng lượng khung sắt là
, trọng lượng khung sắt là ![]() và trọng lượng của chiếc xe ô tô là
và trọng lượng của chiếc xe ô tô là ![]() . Tính cường độ lực căng của mỗi đoạn dây cáp (làm tròn kết quả đến hàng đơn vị).
. Tính cường độ lực căng của mỗi đoạn dây cáp (làm tròn kết quả đến hàng đơn vị).