Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 15)
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Hàm số nào dưới đây có đồ thị như hình sau?
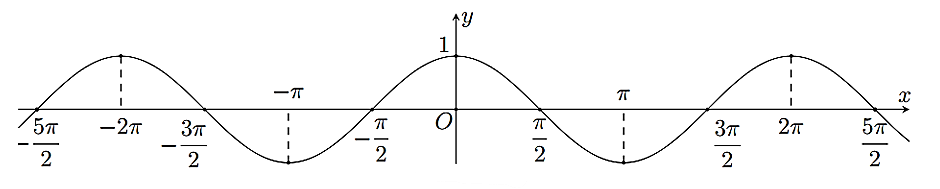
A.![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
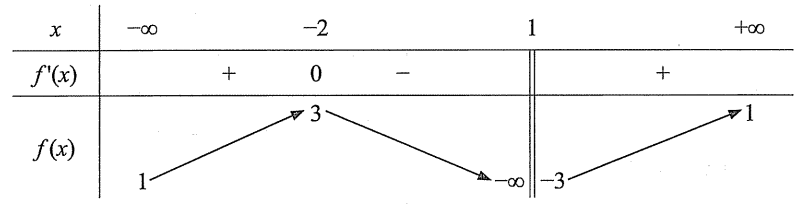
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tích phân 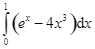 bằng:
bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
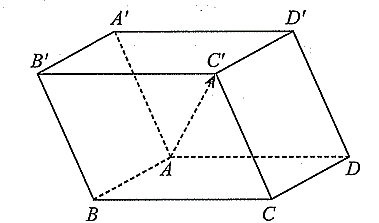
Cho hình hộp ![]() như hình bên.
như hình bên.
Phát biểu nào sau đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , đường thẳng
, đường thẳng ![]() có một vectơ chỉ phương là:
có một vectơ chỉ phương là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , phương trình nào sau đây là phương trình của mặt cầu có tâm
, phương trình nào sau đây là phương trình của mặt cầu có tâm ![]() và bán kính
và bán kính ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Nếu hàm số ![]() liên tục trên
liên tục trên ![]() thoả mãn
thoả mãn 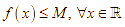 và tồn tại
và tồn tại ![]() sao cho
sao cho ![]() thì:
thì:
Hàm sốđạt giá trị lớn nhất bằng ![]() .
.
Hàm sốđạt giá trị cực tiểu bằng ![]() .
.
Hàm sốđạt giá trị nhỏ nhất bằng ![]() .
.
Hàm sốđạt giá trị cực đại bằng ![]() .
.
Trong không gian ![]() , toạ độ của vectơ
, toạ độ của vectơ ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tập nghiệm của bất phương trình ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , đường thẳng đi qua hai điểm
, đường thẳng đi qua hai điểm ![]() và
và ![]() có phương trình tham số là:
có phương trình tham số là:
A. 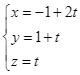 .
.
B. 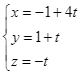 .
.
C. 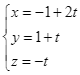 .
.
D. 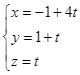 .
.
Một mẫu số liệu ghép nhóm về chiều cao của một lớp (đơn vị là centimét) có phương sai là ![]() . Độ lệch chuẩn của mẫu số liệu đó bằng:
. Độ lệch chuẩn của mẫu số liệu đó bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() thoả mãn
thoả mãn ![]() và
và ![]() . Phương trình tiếp tuyến của đồ thị hàm số
. Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm
tại điểm ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() .
.
a) Đạo hàm của hàm số đã cho là 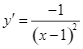 .
.
b) Đạo hàm của hàm số đã cho nhận giá trị âm với mọi ![]() .
.
c) Bảng biến thiên của hàm số đã cho là:
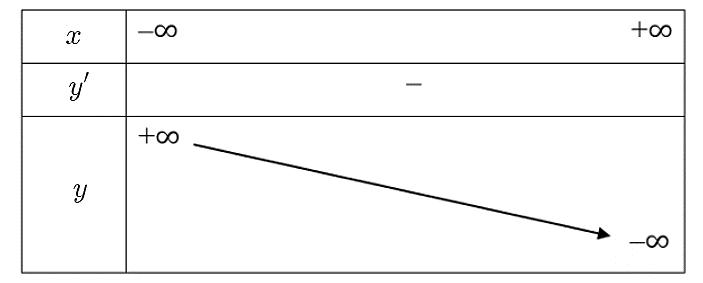
d) Đồ thị của hàm số đã cho như ở hình dưới đây.
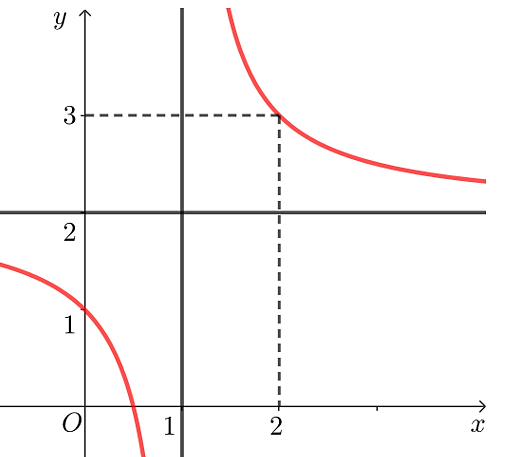
Trong không gian với hệ trục tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() đi qua hai điểm
đi qua hai điểm ![]() và
và ![]() , mặt phẳng
, mặt phẳng ![]() đi qua ba điểm
đi qua ba điểm ![]() .
.
a) Vectơ ![]() không là vectơ chỉ phương của đường thẳng
không là vectơ chỉ phương của đường thẳng ![]() .
.
b) ![]() ,
, ![]() .
.
c) Mặt phẳng ![]() có một vectơ pháp tuyến có tọa độ là
có một vectơ pháp tuyến có tọa độ là ![]() .
.
d) Góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() .
.
Cho hàm số 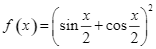 .
.
a) ![]() .
.
b) ![]() liên tục trên
liên tục trên ![]() .
.
c) ![]() .
.
d) ![]() .
.
Một két nước ngọt đựng 24 chai nước có khối lượng và hình thức bề ngoài như nhau, trong đó có 16 chai loại I và 8 chai loại II. Bác Tùng lần lượt lấy ra ngẫu nhiên hai chai (lấy không hoàn lại). Xét các biến cố:
A: “Lần thứ nhất lấy ra chai nước loại I”;
B: “Lần thứ hai lấy ra chai nước loại I”.
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
d) ![]() .
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Cho tứ diện đều ![]() cạnh 10 cm. Gọi
cạnh 10 cm. Gọi ![]() là các điểm lần lượt thuộc các cạnh
là các điểm lần lượt thuộc các cạnh ![]() sao cho
sao cho ![]() . Tính thể tích của khối chóp cụt đều
. Tính thể tích của khối chóp cụt đều ![]() (kết quả làm tròn đến hàng phần chục theo đơn vị centimét khối).
(kết quả làm tròn đến hàng phần chục theo đơn vị centimét khối).
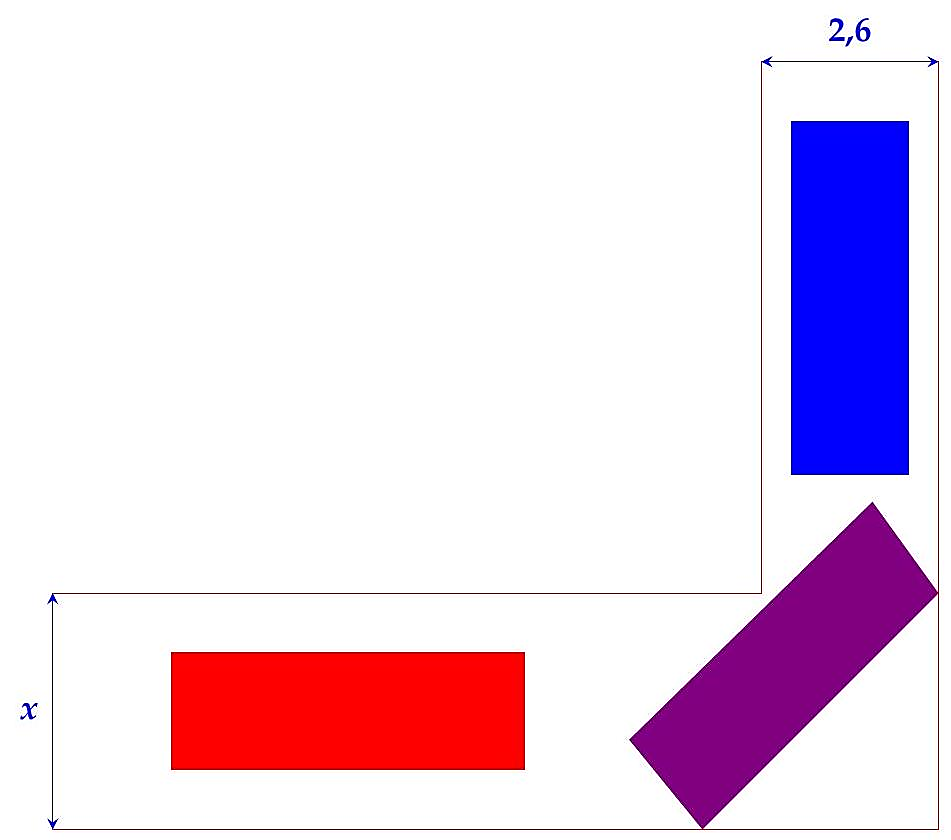
Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ô tô nhà thầy Anh. Đoạn đường đầu tiên có chiều rộng bằng ![]() , đoạn đường thẳng vào cổng GARA có chiều rộng
, đoạn đường thẳng vào cổng GARA có chiều rộng ![]() . Biết kích thước xe ô tô là
. Biết kích thước xe ô tô là ![]() . Để tính toán và thiết kế đường đi cho ô tô người ta coi ô tô như một khối hộp chữ nhật có kích thước chiều dài
. Để tính toán và thiết kế đường đi cho ô tô người ta coi ô tô như một khối hộp chữ nhật có kích thước chiều dài ![]() , chiều rộng
, chiều rộng ![]() . Hỏi chiều rộng nhỏ nhất của đoạn đường đầu tiên bằng bao nhiêu mét để ô tô có thể đi vào GARA được (làm tròn kết quả đến chữ số thập phân thứ nhất)?
. Hỏi chiều rộng nhỏ nhất của đoạn đường đầu tiên bằng bao nhiêu mét để ô tô có thể đi vào GARA được (làm tròn kết quả đến chữ số thập phân thứ nhất)?
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Cự li (m) |
|
|
|
|
|
Tần số | 13 | 45 | 24 | 12 | 6 |
Tính phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Một thùng dầu bị rò rỉ từ lúc 13 giờ với tốc độ rò rỉ là ![]() (lít/giờ), trong đó
(lít/giờ), trong đó ![]() (giờ) là thời gian tính từ khi bắt đầu bị rò rỉ. Khi đó
(giờ) là thời gian tính từ khi bắt đầu bị rò rỉ. Khi đó ![]() (lít) là thể tích dầu bị mất đi thỏa mãn
(lít) là thể tích dầu bị mất đi thỏa mãn ![]() . Giả sử
. Giả sử ![]() là thể tích dầu bị mất đi trong khoảng thời gian từ 13 giờ đến 16 giờ và
là thể tích dầu bị mất đi trong khoảng thời gian từ 13 giờ đến 16 giờ và ![]() là thể tích dầu bị mất đi trong khoảng thời gian từ 16 giờ đến 19 giờ. Tính
là thể tích dầu bị mất đi trong khoảng thời gian từ 16 giờ đến 19 giờ. Tính ![]() (theo đơn vị lít).
(theo đơn vị lít).
Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2 m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài ![]() ;
; ![]() ;
; ![]() . Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ (làm tròn kết quả đến hàng phần chục)?
. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ (làm tròn kết quả đến hàng phần chục)?
Một hãng sản xuất một loại tủ lạnh X ước tính rằng khoảng 80% số người dùng tủ lạnh có đọc quảng cáo tủ lạnh do hãng ấy sản xuất. Trong số những người đọc quảng cáo, có 30% mua loại tủ lạnh X; 10% không đọc quảng cáo cũng mua loại tủ lạnh X. Tính xác suất để một người tiêu dùng đã mua loại tủ lạnh X mà có đọc quảng cáo (làm tròn kết quả đến hàng phần mười).