Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 17)
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chọn một phương án.
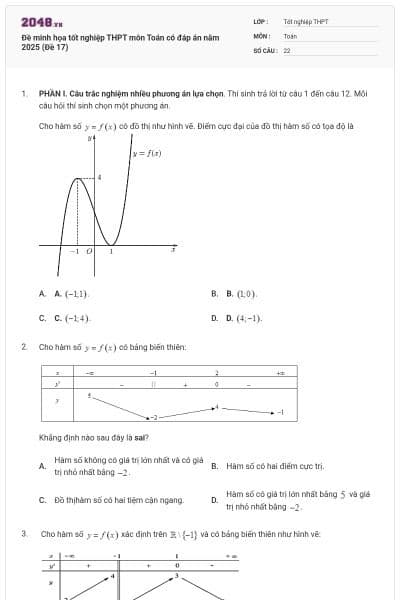
Cho hàm số ![]() có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số có tọa độ là
có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số có tọa độ là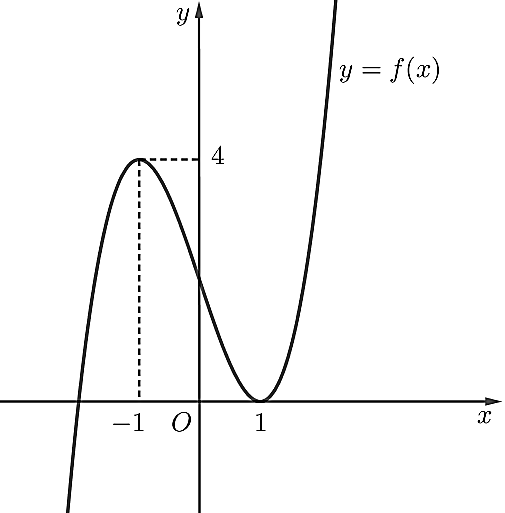
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() có bảng biến thiên:
có bảng biến thiên:
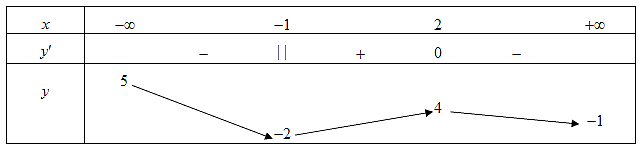
Khẳng định nào sau đây là sai?
Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng ![]() .
.
Hàm số có hai điểm cực trị.
Đồ thịhàm số có hai tiệm cận ngang.
Hàm số có giá trị lớn nhất bằng ![]() và giá trị nhỏ nhất bằng
và giá trị nhỏ nhất bằng ![]() .
.
Cho hàm số ![]() xác định trên
xác định trên ![]() và có bảng biến thiên như hình vẽ:
và có bảng biến thiên như hình vẽ:![]()
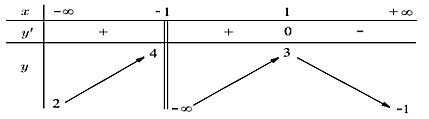
Tổng số tiệm đứng và tiệm cận ngang của đồ thị hàm số đã cho là
2.
0.
3.
1.
Đồ thị hàm số ![]() có tiệm cận xiên là đường thẳng
có tiệm cận xiên là đường thẳng
![]()
![]()
![]()
![]()
Họ tất cả các nguyên hàm của hàm số ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Giả sử 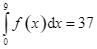 và
và 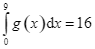 . Khi đó
. Khi đó 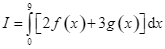 bằng
bằng
![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Bảng sau thống kê khối lượng một số quả măng cụt được lựa chọn ngẫu nhiên trong một thùng hàng.
Khối lượng (gam) |
|
|
|
|
|
Số quả |
|
|
|
|
|
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được cho ở bảng dưới đây.
Nhóm | Giá trị đại diện | Tần số |
| 42,5 | 4 |
| 47,5 | 14 |
| 52,5 | 8 |
| 57,5 | 10 |
| 62,5 | 6 |
| 67,5 | 2 |
|
|
|
Biết số trung bình của mẫu số liệu đã cho là ![]() . Phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười) là
. Phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười) là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ tọa độ ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() . Toạ độ vectơ
. Toạ độ vectơ ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ tọa độ ![]() phương trình mặt phẳng đi qua điểm
phương trình mặt phẳng đi qua điểm ![]() và có vectơ pháp tuyến
và có vectơ pháp tuyến ![]() là:
là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() . Vectơ nào dưới đây là một vectơ chỉ phương của
. Vectơ nào dưới đây là một vectơ chỉ phương của ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ tọa độ ![]() , phương trình nào sau đây là phương trình mặt cầu
, phương trình nào sau đây là phương trình mặt cầu ![]() tâm
tâm ![]() , đi qua điểm
, đi qua điểm ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Theo báo cáo của một cơ sở sản xuất nước tinh khiết, nếu mỗi ngày cơ sở này sản xuất ![]() nước tinh khiết thì phải trả chi phí các khoản sau: 3 triệu đồng chi phí cố định;
nước tinh khiết thì phải trả chi phí các khoản sau: 3 triệu đồng chi phí cố định; ![]() triệu đồng cho mỗi mét khối sản phẩm;
triệu đồng cho mỗi mét khối sản phẩm; ![]() triệu đồng chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là
triệu đồng chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là ![]() . Gọi
. Gọi ![]() là chi phí sản xuất
là chi phí sản xuất ![]() sản phẩm mỗi ngày và
sản phẩm mỗi ngày và ![]() là chi phí trung bình mỗi mét khối sản phẩm.
là chi phí trung bình mỗi mét khối sản phẩm.
a) ![]() (triệu đồng).
(triệu đồng).
b) Chi phí sản xuất ![]() nước tinh khiết là 20 triệu đồng.
nước tinh khiết là 20 triệu đồng.
c) ![]() (triệu đồng).
(triệu đồng).
d) Chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết sản xuất trong ngày là ![]() .
.
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là ![]() và khả năng thắng thầu của dự án 2 là
và khả năng thắng thầu của dự án 2 là ![]() . Khả năng thắng thầu cả 2 dự án là
. Khả năng thắng thầu cả 2 dự án là ![]() .
.
Gọi ![]() là biến cố: “Thắng thầu dự án 1”; gọi
là biến cố: “Thắng thầu dự án 1”; gọi ![]() là biến cố: “Thắng thầu dự án 2”.
là biến cố: “Thắng thầu dự án 2”.
a) ![]() và
và ![]() là hai biến cố độc lập.
là hai biến cố độc lập.
b) Xác suất để công ty thắng thầu đúng 1 dự án bằng ![]() .
.
c) Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là ![]() .
.
d) Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là ![]() .
.
Một chất điểm ![]() xuất phát từ
xuất phát từ ![]() , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật
, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật ![]() , trong đó
, trong đó ![]() (giây) là khoảng thời gian tính từ lúc
(giây) là khoảng thời gian tính từ lúc ![]() bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm ![]() cũng xuất phát từ
cũng xuất phát từ ![]() , chuyển động thẳng cùng hướng với
, chuyển động thẳng cùng hướng với ![]() nhưng chậm hơn 10 giây so với
nhưng chậm hơn 10 giây so với ![]() và có gia tốc bằng
và có gia tốc bằng ![]() (
(![]() là hằng số). Sau khi
là hằng số). Sau khi ![]() xuất phát được 15 giây thì đuổi kịp
xuất phát được 15 giây thì đuổi kịp ![]() .
.
a) Quãng đường chất điểm ![]() đi được cho đến khi hai chất điểm gặp nhau là
đi được cho đến khi hai chất điểm gặp nhau là ![]()
b) Vận tốc của chất điểm ![]() tại thời điểm
tại thời điểm ![]() tính từ lúc
tính từ lúc ![]() xuất phát là
xuất phát là ![]()
c) Quãng đường chất điểm ![]() đi được cho đến khi 2 chất điểm gặp nhau là
đi được cho đến khi 2 chất điểm gặp nhau là ![]()
d) Vận tốc của ![]() tại thời điểm đuổi kịp
tại thời điểm đuổi kịp ![]() là
là ![]()
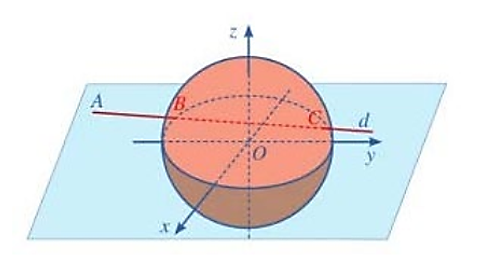
Trong không gian hệ trục tọa độ ![]() (đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu sân bay Cam Ranh – Khánh Hòa ở vị trí
(đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu sân bay Cam Ranh – Khánh Hòa ở vị trí ![]() và được thiết kế phát hiện máy bay ở khoảng cách tối đa 600 km.
và được thiết kế phát hiện máy bay ở khoảng cách tối đa 600 km.
Một máy bay của hãng Việt Nam Airlines đang chuyển động theo đường thẳng ![]() có phương trình
có phương trình 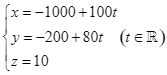 và hướng về đài kiểm soát không lưu (như hình vẽ).
và hướng về đài kiểm soát không lưu (như hình vẽ).
a) Phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phát sóng của đài kiểm soát không lưu trong không gian là ![]() .
.
b) Quãng đường mà máy bay nhận được tín hiệu của đài kiểm soát không lưu là ![]() km.
km.
c) Toạ độ vị trí mà máy bay bay gần đài kiểm soát không lưu nhất là ![]() .
.
d) Khoảng cách ngắn nhất giữa máy bay với đài kiểm soát không lưu xấp xỉ bằng ![]() km.
km.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Hai con tàu ![]() và
và ![]() đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu
đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu ![]() chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu
chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu ![]() chạy về vị trí hiện tại của tàu
chạy về vị trí hiện tại của tàu ![]() với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?
với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc ![]() và có độ lớn lần lượt là
và có độ lớn lần lượt là ![]() N và
N và ![]() N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn
N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn ![]() N. Tính độ lớn của hợp lực của ba lực trên (làm tròn kết quả đến hàng phần chục theo đơn vị Newton).
N. Tính độ lớn của hợp lực của ba lực trên (làm tròn kết quả đến hàng phần chục theo đơn vị Newton).
Cho hình chóp ![]() có đáy
có đáy ![]() là tam giác đều cạnh bằng 2,
là tam giác đều cạnh bằng 2, ![]() vuông góc với mặt phẳng
vuông góc với mặt phẳng ![]() . Góc giữa đường thẳng
. Góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() . Gọi
. Gọi ![]() là trung điểm của cạnh
là trung điểm của cạnh ![]() . Tính khoảng cách từ điểm
. Tính khoảng cách từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]() , kết quả làm tròn đến hàng phần trăm.
, kết quả làm tròn đến hàng phần trăm.
Một bể chứa ![]() lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ
lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ ![]() gam muối cho mỗi lít nước với tốc độ
gam muối cho mỗi lít nước với tốc độ ![]() lít/phút. Giả sử sau
lít/phút. Giả sử sau ![]() phút, nồng độ muối của nước trong bể (tỉ số giữa khối lượng muối trong bể và thể tích nước trong bể, đơn vị gam/lít) là một hàm số
phút, nồng độ muối của nước trong bể (tỉ số giữa khối lượng muối trong bể và thể tích nước trong bể, đơn vị gam/lít) là một hàm số ![]() . Khi lượng nước trong bể tăng theo thời gian đến vô hạn thì nồng độ muối của nước trong bể sẽ tăng dần đến giá trị nào?
. Khi lượng nước trong bể tăng theo thời gian đến vô hạn thì nồng độ muối của nước trong bể sẽ tăng dần đến giá trị nào?
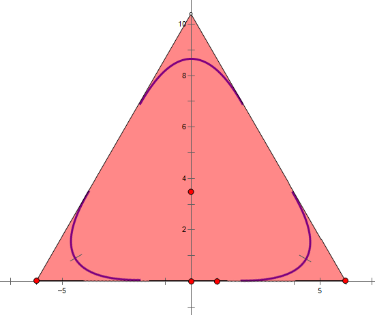
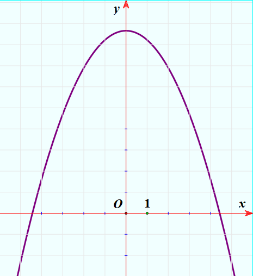
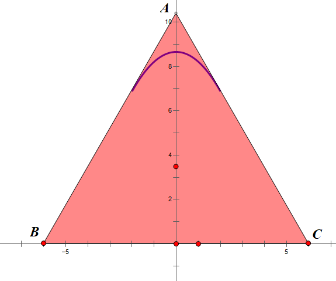
Một tấm kính làm mặt bàn (H1) có hình dáng tam giác đều với 3 đỉnh được làm cong (H2). Biết cạnh tấm kính tam giác ban đầu bằng 12 dm. Để cắt góc bàn được đẹp thì người ta cắt theo đường cong là đường Parabol ![]() (H3) có hai nhánh tiếp giáp với hai cạnh của tam giác (H4).
(H3) có hai nhánh tiếp giáp với hai cạnh của tam giác (H4).
|
|
|
|
H1 | H2 | H3 | H4 |
Khi đó, ta tính được diện tích mặt kính làm mặt bàn (H1) bằng ![]() . Xác định
. Xác định ![]() .
.
Trong một đợt kiểm tra sức khoẻ để khảo sát tình trạng bệnh xơ gan của người dân, tỉ lệ người dân bị bệnh xơ gan là ![]() và
và ![]() trong số đó bị dương tính với viêm gan B. Tuy nhiên, có
trong số đó bị dương tính với viêm gan B. Tuy nhiên, có ![]() những người không bị xơ gan mặc dù dương tính viêm gan B. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó dương tính với viêm gan B. Xác suất người đó bị mắc bệnh xơ gan là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
những người không bị xơ gan mặc dù dương tính viêm gan B. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó dương tính với viêm gan B. Xác suất người đó bị mắc bệnh xơ gan là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?