Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 13)
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
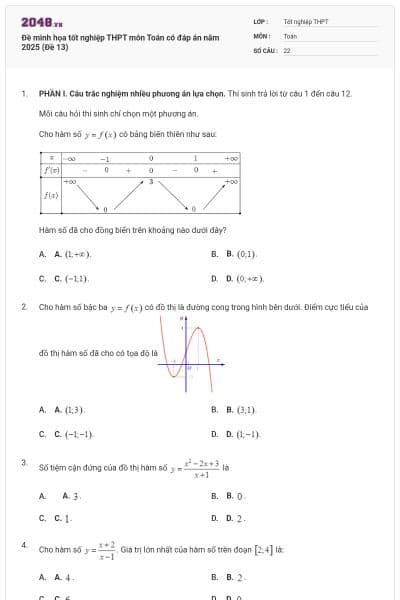
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
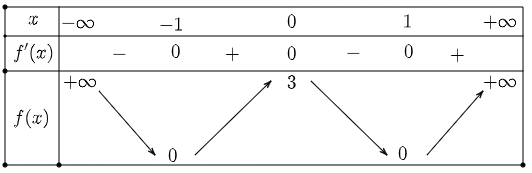
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
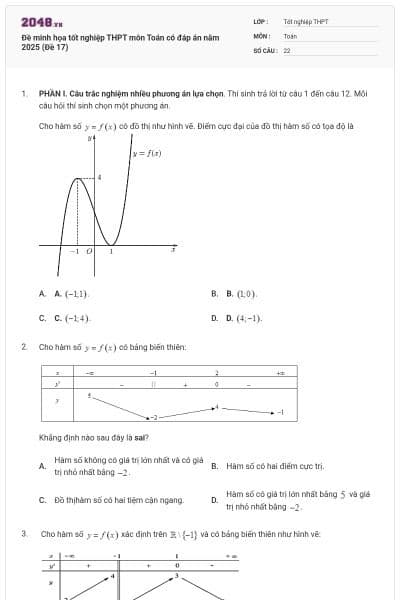
Cho hàm số bậc ba ![]() có đồ thị là đường cong trong hình bên dưới. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
có đồ thị là đường cong trong hình bên dưới. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là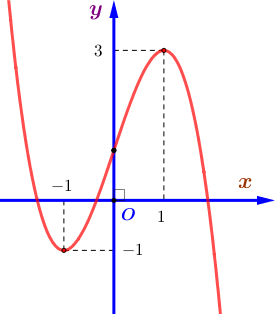
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Số tiệm cận đứng của đồ thị hàm số ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() . Giá trị lớn nhất của hàm số trên đoạn
. Giá trị lớn nhất của hàm số trên đoạn ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ trục tọa độ ![]() , cho
, cho ![]() . Tọa độ của vectơ
. Tọa độ của vectơ ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và nhận vectơ
và nhận vectơ ![]() làm vectơ pháp tuyến có phương trình là
làm vectơ pháp tuyến có phương trình là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , điểm nào dưới đây thuộc đường thẳng
, điểm nào dưới đây thuộc đường thẳng ![]() :
: 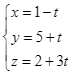 ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() (đơn vị của các trục tọa độ là kilômét), một trạm thu phát sóng điện thoại di động có đầu thu phát được đặt tại điểm
(đơn vị của các trục tọa độ là kilômét), một trạm thu phát sóng điện thoại di động có đầu thu phát được đặt tại điểm ![]() . Cho biết bán kính phủ sóng của trạm là
. Cho biết bán kính phủ sóng của trạm là ![]() . Người sử dụng điện thoại đứng ở điểm nào sau đây thì sử dụng được dịch vụ của trạm nói trên?
. Người sử dụng điện thoại đứng ở điểm nào sau đây thì sử dụng được dịch vụ của trạm nói trên?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là:
0,5.
0,333.
0,2.
0,667.
Thống kê điểm thi đánh giá năng lực của một trường THPT qua thang điểm ![]() đối với môn Toán được cho như bảng sau:
đối với môn Toán được cho như bảng sau:
Điểm |
|
|
|
|
|
Số học sinh |
|
|
|
|
|
Điểm trung bình của tất cả các học sinh tham gia dự thi thuộc đoạn nào sau đây?
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Tìm nguyên hàm của hàm số ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho 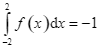 và
và 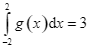 . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?
A. 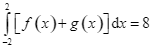 .
.
B. 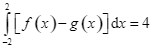 .
.
C. 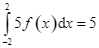 .
.
D. 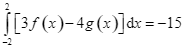 .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() .
.
a) ![]()
b) Đạo hàm của hàm số đã cho là ![]()
c) Nghiệm của phương trình ![]() trên đoạn
trên đoạn ![]() là
là ![]() .
.
d) Giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() là
là ![]() .
.
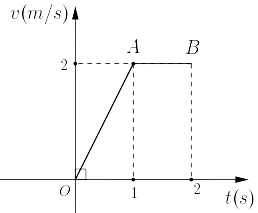
Một vật chuyển động với vận tốc được cho bởi đồ thị trong hình bên.
a) Vận tốc của vật tại thời điểm ![]() được xác định bởi hàm số
được xác định bởi hàm số
 .
.
b) Quãng đường vật đi được trong 1 giây đầu tiên được xác định bởi công thức 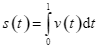 .
.
c) Quãng đường vật đi được trong khoảng thời gian từ 1 giây đến 2 giây được xác định bởi công thức 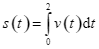 .
.
d) Quãng đường mà vật đi được trong 2 giây đầu tiên là ![]() .
.
Biểu đồ dưới đây biểu thị kết quả thu thập được về mức tiền (đơn vị: tỷ đồng) của một số khách hàng nợ ở hai ngân hàng A và B.
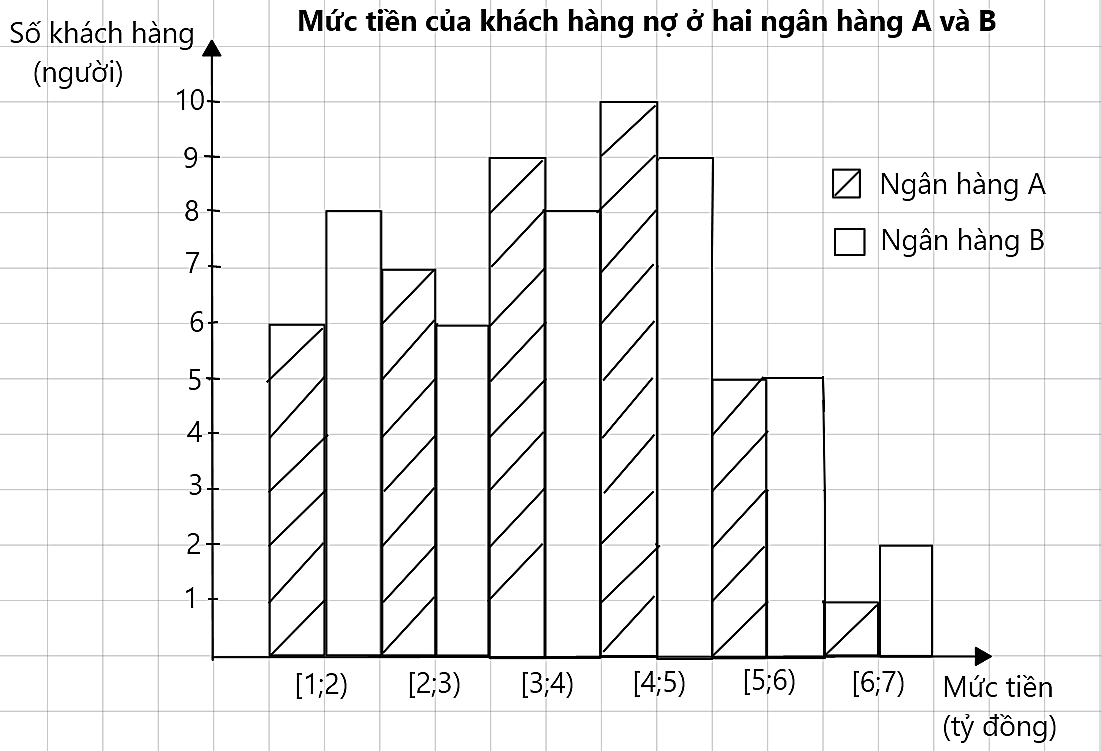
a) Bảng giá trị đại diện cho mỗi nhóm và bảng tần số ghép nhóm cho mẫu số liệu tương ứng với biểu đồ trên như sau:
Mức tiền (tỷ đồng) |
|
|
|
|
|
|
Mức tiền đại diện (tỷ đồng) |
|
|
|
|
|
|
Số khách hàng ngân hàng A |
|
|
|
|
|
|
Số khách hàng ngân hàng B |
|
|
|
|
|
|
b) Độ lệch chuẩn của mẫu số liệu ghép nhóm của ngân hàng A bằng ![]() .
.
c) Độ lệch chuẩn của mẫu số liệu ghép nhóm của ngân hàng B bằng ![]() .
.
d) Người ta dùng độ lệch chuẩn để so sánh mức độ rủi ro của số tiền khách hàng nợ ngân hàng. Ngân hàng nào có độ lệch chuẩn cao hơn thì có độ rủi ro lớn hơn. Theo quan điểm trên, độ rủi ro của ngân hàng A cao hơn ngân hàng B.
Trong không gian với hệ tọa độ ![]() , một cabin cáp treo xuất phát từ điểm
, một cabin cáp treo xuất phát từ điểm ![]() và chuyển động đều theo đường cáp có vectơ chỉ phương là
và chuyển động đều theo đường cáp có vectơ chỉ phương là ![]() với tốc độ là
với tốc độ là ![]() (đơn vị trên mỗi trục tọa độ là mét).
(đơn vị trên mỗi trục tọa độ là mét).
a) Phương trình tham số của đường cáp là: 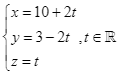 .
.
b) Giả sử sau thời gian ![]() kể từ lúc xuất phát
kể từ lúc xuất phát ![]() , cabin đến điểm
, cabin đến điểm ![]() . Khi đó tọa độ điểm
. Khi đó tọa độ điểm ![]() là
là ![]() .
.
c) Cabin dừng ở điểm ![]() có hoành độ
có hoành độ ![]() , phương trình mặt phẳng đi qua điểm
, phương trình mặt phẳng đi qua điểm ![]() và vuông góc với đường cáp là
và vuông góc với đường cáp là ![]() .
.
d) Đường cáp ![]() tạo với mặt phẳng
tạo với mặt phẳng ![]() một góc
một góc ![]() .
.
PHẦN III. Câu trắc nghiệm trả lời ngắn.Trong khoảng thời gian từ ngày 01/01/2024 đến hết ngày 30/09/2024 nhóm nghiên cứu đã quan sát sự phát triển của một quần thể sinh vật X. Kết quả nghiên cứu chỉ ra rằng, tại ngày thứ ![]() của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số
của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số ![]() (con),
(con), ![]() và ngày 26/09/2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với
và ngày 26/09/2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với ![]() con. Ngày 25/11/2014 số lượng cá thể sinh vật X được ước lượng khoảng bao nhiêu nghìn con (làm tròn kết quả đến hàng phần chục)?
con. Ngày 25/11/2014 số lượng cá thể sinh vật X được ước lượng khoảng bao nhiêu nghìn con (làm tròn kết quả đến hàng phần chục)?
Một bác thợ xây bơm nước vào bể chứa nước. Gọi ![]() là thể tích nước bơm được sau
là thể tích nước bơm được sau ![]() giây. Cho
giây. Cho ![]() và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là
và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là ![]() , sau
, sau ![]() giây thì thể tích nước trong bể là
giây thì thể tích nước trong bể là ![]() . Tính thể tích nước trong bể sau khi bơm được
. Tính thể tích nước trong bể sau khi bơm được ![]() giây (đơn vị: mét khối).
giây (đơn vị: mét khối).
Ba chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Nam ![]() và về phía Đông
và về phía Đông ![]() đồng thời cách mặt đất
đồng thời cách mặt đất ![]() . Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc
. Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc ![]() và về phía Tây
và về phía Tây ![]() đồng thời cách mặt đất
đồng thời cách mặt đất ![]() . Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng. Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó (kết quả làm tròn đến chữ số hàng phần chục theo đơn vị kilômét).
. Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng. Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó (kết quả làm tròn đến chữ số hàng phần chục theo đơn vị kilômét).
Tỉ lệ học sinh tiêm vắc xin phòng bệnh Thủy Đậu trong một trường ![]() là
là ![]() . Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là
. Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là ![]() , còn trong số học sinh chưa tiêm, tỉ lệ mắc bệnh là
, còn trong số học sinh chưa tiêm, tỉ lệ mắc bệnh là ![]() . Gặp ngẫu nhiên một học sinh ở trường đó. Biết học sinh đó bị bệnh Thủy Đậu. Tính xác suất học sinh đó không tiêm vắc xin phòng bệnh Thủy Đậu (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm).
. Gặp ngẫu nhiên một học sinh ở trường đó. Biết học sinh đó bị bệnh Thủy Đậu. Tính xác suất học sinh đó không tiêm vắc xin phòng bệnh Thủy Đậu (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm).
Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất là ![]() năm. Để có được số tiền cả gốc và lãi nhiều hơn 130 triệu đồng thì người đó phải gửi ít nhất bao nhiêu năm? Biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi.
năm. Để có được số tiền cả gốc và lãi nhiều hơn 130 triệu đồng thì người đó phải gửi ít nhất bao nhiêu năm? Biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi.
Trong Hoá học, cấu tạo của phân tử ammonia ![]() có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen
có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen ![]() và đáy là tam giác
và đáy là tam giác ![]() với
với ![]() là vị trí của ba nguyên tử hydrogen
là vị trí của ba nguyên tử hydrogen ![]() . Góc tạo bởi liên kết
. Góc tạo bởi liên kết ![]() , có hai cạnh là hai đoạn thẳng nối
, có hai cạnh là hai đoạn thẳng nối ![]() với hai trong ba điểm
với hai trong ba điểm ![]() (chẳng hạn như
(chẳng hạn như ![]() ), được gọi là góc liên kết của phân tử
), được gọi là góc liên kết của phân tử ![]() . Góc này xấp xỉ 107°. (Nguồn: https://en.wikipedia.org/wiki/Ammonia).
. Góc này xấp xỉ 107°. (Nguồn: https://en.wikipedia.org/wiki/Ammonia).
Trong không gian ![]() , cho một phân tử
, cho một phân tử ![]() được biểu diễn bởi hình chóp tam giác đều
được biểu diễn bởi hình chóp tam giác đều ![]() với
với ![]() là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm
là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm ![]() thuộc trục
thuộc trục ![]() , ba nguyên tử hydrogen ở các vị trí
, ba nguyên tử hydrogen ở các vị trí ![]() , trong đó
, trong đó ![]() và
và ![]() song song với trục
song song với trục ![]() (xem hình vẽ). Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen (làm tròn các kết quả tính toán đến hàng phần trăm).
(xem hình vẽ). Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen (làm tròn các kết quả tính toán đến hàng phần trăm).