Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 10)
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho ![]() và
và ![]() là hai biến cố đối nhau. Chọn câu đúng.
là hai biến cố đối nhau. Chọn câu đúng.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Một vật được phóng thẳng đứng lên trên từ mặt đất với tốc độ ban đầu là ![]() m/s (bỏ qua sức cản của không khí), độ cao (tính bằng mét) của vật sau
m/s (bỏ qua sức cản của không khí), độ cao (tính bằng mét) của vật sau ![]() giây được cho bởi công thức
giây được cho bởi công thức ![]() . Vận tốc của vật sau 3 giây bằng
. Vận tốc của vật sau 3 giây bằng
53,4 (m/s).
32,5 (m/s).
3,1 (m/s).
4,9 (m/s).
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
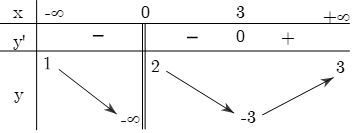
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
2.
3.
4.
1
Trong mặt phẳng tọa độ ![]() , cho
, cho ![]() ,
, ![]() , khi đó tọa độ
, khi đó tọa độ ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Mỗi ngày bà Minh đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bà Minh trong 20 ngày được thống kê lại ở bảng sau:
Quãng đường (km) |
|
|
|
|
|
Số ngày | 3 | 6 | 5 | 4 | 2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm là
1,5.
0,9.
0,6.
0,3.
Chọn khẳng định sai.
Phương sai của MSL ghép nhóm là giá trị xấp xỉ cho phương sai của MSL gốc.
Độ lệch chuẩn của MSL ghép nhóm cũng là giá trị xấp xỉ cho độ lệch chuẩn của MSL gốc.
Phương sai và độ lệch chuẩn càng nhỏ thì dữ liệu càng phân tán.
Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.
Cho hàm số ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() thỏa mãn
thỏa mãn ![]() . Tìm
. Tìm ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có
và có 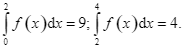 Tính
Tính 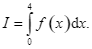
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Diện tích ![]() của hình phẳng giới hạn bởi các đường
của hình phẳng giới hạn bởi các đường ![]() ,
,![]() ,
, ![]() và
và ![]() được tính bởi công thức nào sau đây?
được tính bởi công thức nào sau đây?
A. 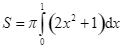 .
.
B. 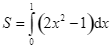 .
.
C. 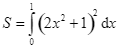 .
.
D. 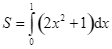 .
.
Trong không gian ![]() , cho mặt cầu
, cho mặt cầu ![]() . Tính bán kính
. Tính bán kính ![]() của mặt cầu
của mặt cầu ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Phương trình ![]() có nghiệm là
có nghiệm là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Nghiệm của phương trình ![]() là
là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() có đồ thị là
có đồ thị là ![]() .
.
a) Phương trình tiếp tuyến có hệ số góc nhỏ nhất của đồ thị ![]() đi qua điểm
đi qua điểm ![]() .
.
b) Trên đoạn ![]() thì giá trị lớn nhất của hàm số đạt được tại
thì giá trị lớn nhất của hàm số đạt được tại ![]() .
.
c) Tâm đối xứng của đồ thị hàm số có tọa độ là ![]() .
.
d) Đồ thị hàm số có 2 điểm cực trị.

Cho hình hộp chữ nhật ![]() có
có ![]() ,
, ![]() và đặt
và đặt ![]()
![]() . Lấy điểm
. Lấy điểm ![]() thỏa mãn
thỏa mãn ![]() và điểm
và điểm ![]() thỏa mãn
thỏa mãn ![]() (tham khảo hình vẽ bên).
(tham khảo hình vẽ bên).
a) ![]() .
.
b) ![]() .
.
c) ![]() với
với ![]() là các số thực.
là các số thực.
d) ![]() .
.
Trong không gian toạ độ ![]() cho đường thẳng
cho đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]()
a) Vectơ có toạ độ ![]() là một vectơ chỉ phương của
là một vectơ chỉ phương của ![]()
b) Vectơ có toạ độ ![]() là một vectơ pháp tuyến của
là một vectơ pháp tuyến của ![]()
c) Phương trình mặt phẳng ![]() đi qua
đi qua ![]() và vuông góc với
và vuông góc với ![]() là
là ![]() .
.
d) Góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() (làm tròn đến hàng đơn vị của độ) bằng
(làm tròn đến hàng đơn vị của độ) bằng ![]()
Ở huyện Đông Anh, Hà Nội, vào tháng 7, người ta đo được xác suất để có mưa vào thứ hai là ![]() . Nếu trời có mưa vào thứ hai thì xác suất để có mưa vào thứ ba là
. Nếu trời có mưa vào thứ hai thì xác suất để có mưa vào thứ ba là ![]() . Nếu thứ hai không có mưa thì xác suất để có mưa vào thứ ba là
. Nếu thứ hai không có mưa thì xác suất để có mưa vào thứ ba là ![]() .
.
a) Biểu thức theo biến ![]() cho biết xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là
cho biết xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là ![]()
b) Khả năng trời sẽ có mưa vào cả thứ hai và thứ ba là ![]() khi
khi ![]() .
.
c) Biểu thức theo biến ![]() , cho biết xác suất để trời sẽ mưa vào thứ ba là
, cho biết xác suất để trời sẽ mưa vào thứ ba là ![]() .
.
d) Xác suất để có mưa vào thứ hai với điều kiện của biến ![]() thỏa mãn xác suất trời sẽ mưa vào thứ ba lớn nhất bằng
thỏa mãn xác suất trời sẽ mưa vào thứ ba lớn nhất bằng ![]() .
.
PHẦN III. Câu trắc nghiệm trả lời ngắnMột đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu nghìn đồng để doanh thu từ tiền bán vé là lớn nhất?
Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là ![]() triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm
triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm ![]() đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận được sau ba năm làm việc cho công ty (đơn vị: triệu đồng).
đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận được sau ba năm làm việc cho công ty (đơn vị: triệu đồng).
Cho hình chóp ![]() có đáy là hình thoi cạnh bằng
có đáy là hình thoi cạnh bằng ![]() ,
, ![]() . Mặt bên
. Mặt bên ![]() là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Khoảng cách giữa hai đường thẳng
. Khoảng cách giữa hai đường thẳng ![]() và
và ![]() bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Có ![]() đội thi đấu bơi lội. Đội I có
đội thi đấu bơi lội. Đội I có ![]() vận động viên, đội II có
vận động viên, đội II có ![]() vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là
vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là ![]() và
và ![]() . Chọn ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I (làm tròn kết quả đến hàng phần trăm).
. Chọn ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I (làm tròn kết quả đến hàng phần trăm).
Một viên gạch hoa hình vuông cạnh ![]() . Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng
. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng ![]() , khi đó giá trị của biểu thức
, khi đó giá trị của biểu thức ![]() bằng bao nhiêu?
bằng bao nhiêu?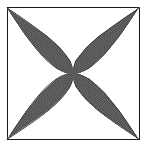
Trong không gian với hệ tọa độ ![]() (đơn vị đo lấy theo kilômét), một Radar phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm
(đơn vị đo lấy theo kilômét), một Radar phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm ![]() đến điểm
đến điểm ![]() trong 10 phút.
trong 10 phút.
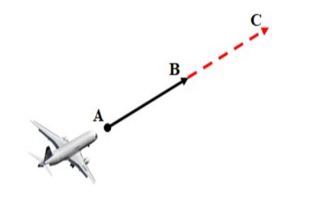
Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là ![]() . Khi đó
. Khi đó ![]() bằng bao nhiêu?
bằng bao nhiêu?