Đề kiểm tra Tích vô hướng của hai vectơ (có lời giải) - Đề 3

Cho hình vuông \(ABCD\) tâm \(O\). Hỏi mệnh đề nào sau đây sai?

Cho hình vuông \(ABCD\) cạnh \(a\). Hỏi mệnh đề nào sau đây sai?

Cho hình thang vuông \(ABCD\)có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\); \(I\) là trung điểm của \(AD\). Khi đó \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \) bằng :

Cho tam giác \(ABC\) vuông tại \(A\) có \(\hat B = {60^{\rm{o}}}\),\(AB = a\). Tính \(\overrightarrow {AC} .\overrightarrow {CB} \)

Cho 2 vectơ đơn vị \(\vec a\) và \(\vec b\) thỏa\(\left| {\vec a + \vec b} \right| = 2\). Hãy xác định \(\left( {3\vec a - 4\vec b} \right)\left( {2\vec a + 5\vec b} \right)\)

Cho hình thang vuông \(ABCD\)có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\).Tính \(\overrightarrow {DA} .\overrightarrow {BC} \)

Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 9\), \(BC = 5\). Tính \(\overrightarrow {AB} .\overrightarrow {AC} \)

Cho ba điểm \(A,B,C\) thỏa \(AB = 2{\mkern 1mu} {\mkern 1mu} {\rm{cm}},{\rm{ }}BC = 3{\mkern 1mu} {\mkern 1mu} {\rm{cm, }}CA = 5{\mkern 1mu} {\mkern 1mu} {\rm{cm}}\) Tính \(\overrightarrow {CA} .\overrightarrow {CB} \)

Cho tam giác \(ABC\) có \[BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c\] Tính \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {BC} \)

Cho hình vuông \[ABCD\] cạnh \[a\]. Tính \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right)\)

Cho tam giác \[ABC\] có \[BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c.\] Gọi \[M\] là trung điểm cạnh \[BC.\]Đẳng thức nào sau đây đúng?

Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = a,BC = 2a\). Khi đó:

a) $\widehat{ACB}={60}^{°}$

b) \(\overrightarrow {BA}  \cdot \overrightarrow {BC}  = {a^2}\)

c) \(\overrightarrow {BC}  \cdot \overrightarrow {CA}  = 3{a^2}.\)

d) \(\overrightarrow {AB}  \cdot \overrightarrow {BC}  + \overrightarrow {BC}  \cdot \overrightarrow {CA}  + \overrightarrow {CA}  \cdot \overrightarrow {AB}  =  - 4{a^2}\)

Cho hình vuông \(ABCD\) tâm \(O\), có cạnh \(a\). Biết \(M\) là trung điểm của \(AB,G\) là trọng tâm tam giác \(ADM\). Khi đó:

a) \(\overrightarrow {AB}  \cdot \overrightarrow {CA}  = {a^2}\)

b) \(\overrightarrow {AM}  \cdot \overrightarrow {AC}  = \frac{{{a^2}}}{3}\)

c) \(\overrightarrow {AD}  \cdot \overrightarrow {BD}  + \overrightarrow {OM}  \cdot \overrightarrow {AC}  = \frac{{{a^2}}}{2}\)

d) \((\overrightarrow {AB}  + \overrightarrow {AD} )(\overrightarrow {BD}  + \overrightarrow {BC} ) = {a^2}\)

Cho hình vuông \(ABCD\) tâm \(O\), cạnh bằng \(a\). Khi đó:

a) \(\overrightarrow {AB}  \cdot \overrightarrow {DC}  = 2{a^2}\);

b) \(\overrightarrow {AB}  \cdot \overrightarrow {OC}  = {a^2}\);

c) \(\overrightarrow {CA}  \cdot \overrightarrow {OC}  =  - {a^2}\);

d) \((\overrightarrow {AB}  + \overrightarrow {AD} ) \cdot (\overrightarrow {BC}  + \overrightarrow {BD} ) = {a^2}\)

Cho hình thang \(ABCD\) vuông tại \(A\) và \(B\), biết \(AD = a,BC = 3a\) và cạnh \(AB = 2a\). Khi đó:

a) \(\overrightarrow {AB}  \cdot \overrightarrow {BD}  =  - 4{a^2}\)

b) \(\overrightarrow {BC}  \cdot \overrightarrow {BD}  = 2{a^2}\)

c) \(\overrightarrow {AC}  \cdot \overrightarrow {BD}  =  - 2{a^2}\)

d) Gọi \(I,J\) lần lượt là trung điểm của \(AB,CD\). Khi đó\(\overrightarrow {AC}  \cdot \overrightarrow {IJ}  = 6{a^2}\)

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6

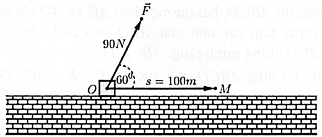
Một người dùng một lực \(\vec F\) có độ lớn \(90\;N\) làm một vật dịch chuyển một đoạn \(100\;m\). Biết lực \(\vec F\) hợp với hướng dịch chuyển một góc \({60^^\circ }\). Tính công sinh ra bởi lực \(\vec F\).

Cho tứ giác lồi \(ABCD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Gọi \(H\) và \(K\) lần lượt là trực tâm các tam giác \(ABO\) và \(CDO\). Gọi \(I,J\) lần lượt là trung điểm \(AD\) và \(BC\). Tính \(\overrightarrow {HK}  \cdot \overrightarrow {IJ} \)?

Cho hình chữ nhật \(ABCD\). Kẻ \(BK \bot AC,K \in AC\). Gọi \(M,N\) lần lượt là trung điểm của \(AK\) và \(CD\). Tìm số đo góc \(\widehat {BMN}\).

Cho đoạn \(AB = 20\). Tồn tại điểm \(M\) sao cho \(T = 3M{A^2} + 2M{B^2}\) đạt giá trị bé nhất \({T_{\min }}\). Tính giá trị \({T_{\min }}\)?

Một chiếc xe được kéo bởi một lực \(\vec F\) có độ lớn \(50\;N\), di chuyển theo quãng đường từ \(A\) đến \(B\) có chiều dài \(200\;m\). Cho biết góc hợp bởi lực \(\vec F\) và \(\overrightarrow {AB} \) bằng ${30}^{°}$ và lực \(\vec F\) được phân tích thành hai lực \({\vec F_1},{\vec F_2}\). Tính công sinh ra bởi các lực \(\vec F,{\vec F_1},\overrightarrow {{F_2}} \)?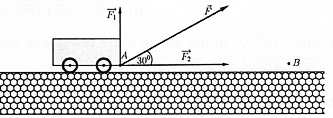

Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AC = 7\;cm\) và \(BC = 14\;cm\).

Tính côsin của góc giữa hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \).