Đề kiểm tra Tích vô hướng của hai vectơ (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
\(\alpha = {180^{\rm{o}}}\).
\(\alpha = {0^{\rm{o}}}\).
\(\alpha = {90^{\rm{o}}}\).
\(\alpha = {45^{\rm{o}}}\).
Cho hai vectơ \(\vec a\) và \(\vec b\) thỏa mãn \(\left| {\vec a} \right| = 3,\)\(\left| {\vec b} \right| = 2\) và \(\vec a.\vec b = - 3.\) Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b.\)
\(\alpha = {30^{\rm{o}}}\).
\(\alpha = {45^{\rm{o}}}\).
\(\alpha = {60^{\rm{o}}}\).
\(\alpha = {120^{\rm{o}}}\).
Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} .\)
\(\overrightarrow {AB} .\overrightarrow {AC} = 2{a^2}.\)
\(\overrightarrow {AB} .\overrightarrow {AC} = - \frac{{{a^2}\sqrt 3 }}{2}\)
\(\overrightarrow {AB} .\overrightarrow {AC} = - \frac{{{a^2}}}{2}\)
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\)
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
\(\overrightarrow a .\overrightarrow b = 0\).
\(\overrightarrow a .\overrightarrow b = - 1\).
\(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
Tam giác \(ABC\) vuông ở \(A\) và có góc \(\widehat B = {50^{\rm{o}}}\). Hệ thức nào sau đây là sai?
\(\left( {\overrightarrow {AB} ,{\rm{ }}\overrightarrow {BC} } \right) = {130^{\rm{o}}}\).
\(\left( {\overrightarrow {BC} ,{\rm{ }}\overrightarrow {AC} } \right) = {40^{\rm{o}}}\).
\(\left( {\overrightarrow {AB} ,{\rm{ }}\overrightarrow {CB} } \right) = {50^{\rm{o}}}\).
\(\left( {\overrightarrow {AC} ,{\rm{ }}\overrightarrow {CB} } \right) = {120^{\rm{o}}}\)
Cho hình vuông \(ABCD\), tính \[{\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right)\]
\(\frac{1}{2}\).
\( - \frac{1}{2}\).
\(\frac{{\sqrt 2 }}{2}\).
\( - \frac{{\sqrt 2 }}{2}\).
Cho tam giác\(ABC\) vuông cân tại \(A\) có \(BC = a\sqrt 2 \).Tính \(\overrightarrow {CA} .\overrightarrow {CB} \)
\(\overrightarrow {CA} .\overrightarrow {CB} = {a^2}\).
\(\overrightarrow {CA} .\overrightarrow {CB} = a\).
\(\overrightarrow {CA} .\overrightarrow {CB} = \frac{{a\sqrt 2 }}{2}\).
\(\overrightarrow {CA} .\overrightarrow {CB} = a\sqrt 2 \).
Cho hình vuông \(ABCD\) có cạnh \(a\). Tính \[\overrightarrow {AB} .\overrightarrow {AD} \,\,\,\]
\[0\].
\(a\).
\(\frac{{{\user2{a}^2}}}{2}\).
\({a^2}\).
Cho hai vectơ \(\overrightarrow a \)và \(\vec b\). Biết \(\left| {\vec a} \right|\) =2, \(\left| {\vec b} \right|\)= \(\sqrt 3 \) và \(\left( {\vec a,\vec b} \right) = {120^{\rm{o}}}\).Tính\(\left| {\vec a + \vec b} \right|\)
\(\sqrt {7 + \sqrt 3 } \).
\(\sqrt {7 - \sqrt 3 } \).
\(\sqrt {7 - 2\sqrt 3 } \).
\(\sqrt {7 + 2\sqrt 3 } \).
Cho hai điểm \(B,C\) phân biệt. Tập hợp những điểm \(M\)thỏa mãn \(\overrightarrow {CM} .\overrightarrow {CB} = {\overrightarrow {CM} ^2}\) là :
Đường tròn đường kính\(BC\).
Đường tròn\(\left( {B;BC} \right)\).
Đường tròn \(\left( {C;CB} \right)\).
Một đường khác.
Cho ba điểm \(A,B,C\) phân biệt. Tập hợp những điểm \(M\) mà \(\overrightarrow {CM} .\overrightarrow {CB} = \overrightarrow {CA} .\overrightarrow {CB} \)là :
Đường tròn đường kính\(AB\).
Đường thẳng đi qua \(A\) và vuông góc với\(BC\).
Đường thẳng đi qua \(B\) và vuông góc với\(AC\).
Đường thẳng đi qua \(C\) và vuông góc với\(AB\).
Cho hai điểm \(A\left( {2,2} \right)\), \(B\left( {5, - 2} \right)\). Tìm \(M\) trên tia \(Ox\) sao cho \(\widehat {AMB{\rm{ }}} = {\rm{ }}{90^{\rm{o}}}\)
\(M\left( {1,6} \right)\).
\(M\left( {6,0} \right)\).
\(M\left( {1,0} \right)\) hay \(M\left( {6,0} \right)\).
\(M\left( {0,1} \right)\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong mặt phẳng tọa độ \(Oxy\), cho các vectơ \(\vec a = ( - 2;3),\vec b = (4;1)\). Khi đó:
a) \(\vec a(\vec a - \vec b) = 12\)
b) \((\vec a + \vec b)(2\vec a - \vec b) = 4\)
c) Vectơ \(\vec c = m\vec i + \vec j\) vuông góc với \(\vec a\) khi \(m = \frac{3}{2}\)
d) Tọa độ vectơ \(\vec d\) sao cho \(\vec a.\vec d = 4,\vec b.\vec d = - 2\) bằng \(\left( { - \frac{5}{7};\frac{6}{7}} \right)\)
Trong mặt phẳng tọa độ \(Oxy\), cho các vectơ \(\vec a = (2;5),\vec b = (3; - 7)\), \(\vec c = (1;1)\). Khi đó:
a) \(\overrightarrow a .\overrightarrow b = 29\)
b) \((\vec a,\vec b) = 15^\circ \)
c) \((\vec a,\vec c) \approx 23,1986^\circ \)
d) Để \(\vec d = (4x + 1)\vec i + (x + 4)\vec j\) tạo với vectơ \(\vec c\) một góc \(45^\circ \) thì \(x = - \frac{1}{4}.\)
Cho hình chữ nhật \(ABCD,AB = 4a,AD = 3a\). Gọi \(M\) là trung điểm của \(AB,G\) là trọng tâm tam giác \(ACM\) (Hình).
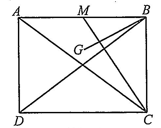
a) \(\overrightarrow {CM} = \frac{1}{2}\overrightarrow {BA} - 3\overrightarrow {BC} \)
b) \(\overrightarrow {BG} = \frac{3}{2}\overrightarrow {BA} + \frac{1}{3}\overrightarrow {BC} .\)
c) \(\overrightarrow {BC} \cdot \overrightarrow {BA} = 0\)
d) \(\overrightarrow {BG} \cdot \overrightarrow {CM} = - {a^2}.\)
Cho hai vectơ . Khi đó:
a) \(\vec a \cdot \vec b = - 6\sqrt 3 \)
b) \((\vec a + \vec b) \cdot (\vec a - \vec b) = 7.\)
c) \((3\vec a + \vec b) \cdot (\vec a - 2\vec b) = - 5 + 30\sqrt 3 \)
d) \((3\vec a + \vec b) \cdot (\vec a - 2\vec b) = 5 + 30\sqrt 3 \)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho hình thang vuông \(ABCD\) có đáy lớn \(AB = 8a\); đáy nhỏ \(CD = 4a\); đường cao \(AD = 6a\); \[I\] là trung điểm của \(AD\). Tính \((\overrightarrow {IA} + \overrightarrow {IB} ) \cdot \overrightarrow {ID} \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = a,AC = 2\sqrt 3 a\) và \(AM\) là trung tuyến. Tính tích vô hướng \(\overrightarrow {BA} \cdot \overrightarrow {AM} \).
Cho \(A(1;2)\) và \(B( - 1;3)\). Cho điểm \(P(0,b)\). Tính \(\cos APB\) theo tung độ của \(P\).
Cho tam giác \(ABC\), trung tuyến \(AM\). Khi đó \(\overrightarrow {AB} \cdot \overrightarrow {AC} = A{M^2} - kB{C^2}.\) Vậy \(k = ?\)
Cho hình vuông \(ABCD\); \(E\) là trung điểm của \(AB,F\) là điểm sao cho \(\overrightarrow {AF} = \frac{1}{3}\overrightarrow {AD} \). Xác định vị trí của điểm \(M\) trên đường thẳng \(BC\) sao cho \(\widehat {EFM} = {90^^\circ }\).
Cho tam giác \(ABC\) cân tại \(A;M\) là trung điểm của \(BC,H\) là hình chiếu của \(M\) trên \(AC;E\) là trung điểm của \(MH\). Tính \(\overrightarrow {AE} .\overrightarrow {BH} \)








