Đề kiểm tra Tích vô hướng của hai vectơ (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hình vuông \[ABCD\] cạnh \[a.\] Đẳng thức nào sau đây đúng?
\(\overrightarrow {AB} .\overrightarrow {AC} = {a^2}\)
\(\overrightarrow {AB} .\overrightarrow {AC} = {a^2}\sqrt 2 \)
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{\sqrt 2 }}{2}{a^2}\)
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}\)
Cho hình vuông \[ABCD\] cạnh \[a\]. Gọi \[E\] là điểm đối xứng của \[D\] qua \[C.\] Đẳng thức nào sau đây đúng?
\(\overrightarrow {AE} .\overrightarrow {AB} = 2{a^2}.\)
\(\overrightarrow {AE} .\overrightarrow {AB} = \sqrt 3 {a^2}.\)
\(\overrightarrow {AE} .\overrightarrow {AB} = \sqrt 5 {a^2}.\)
\(\overrightarrow {AE} .\overrightarrow {AB} = 5{a^2}.\)
Cho tam giác \(ABC\). Tập hợp các điểm \(M\) thỏa mãn \(\overrightarrow {MA} .\overrightarrow {BC} = 0\) là:
một điểm.
đường thẳng.
đoạn thẳng.
đường tròn.
Cho tam giác đều \(ABC\) cạnh \(a = 2\). Hỏi mệnh đề nào sau đây sai?
\(\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)\overrightarrow {BC} = 2\overrightarrow {BC} \).
\(\overrightarrow {BC} .\overrightarrow {CA} = - 2\).
\(\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right).\overrightarrow {AC} = - 4\).
\(\left( {\overrightarrow {BC} - \overrightarrow {AC} } \right).\overrightarrow {BA} = 2\).
Cho \(M\) là trung điểm \(AB\), tìm biểu thức sai:
\[\overrightarrow {MA} .\overrightarrow {AB} = - MA.AB\].
\[\overrightarrow {MA} .\overrightarrow {MB} = - MA.MB\].
\[\overrightarrow {AM} .\overrightarrow {AB} = AM.AB\].
\[\overrightarrow {MA} .\overrightarrow {MB} = MA.MB\].
Cho tam giác đều \(ABC\) cạnh bằng \(a\) và \(H\) là trung điểm \(BC\). Tính \(\overrightarrow {AH} .\overrightarrow {CA} \)
\(\frac{{3{a^2}}}{4}\).
\(\frac{{ - 3{a^2}}}{4}\).
\(\frac{{3{a^2}}}{2}\).
\(\frac{{ - 3{a^2}}}{2}\).
Biết\(\vec a\), \(\vec b\)\( \ne \vec 0\) và \(\vec a.\vec b = - \left| {\vec a} \right|.\left| {\vec b} \right|\). Câu nào sau đây đúng
\(\overrightarrow a \)và \(\overrightarrow b \) cùng hướng.
\(\overrightarrow a \)và \(\overrightarrow b \)nằm trên hai dường thẳng hợp với nhau một góc \({120^{\rm{o}}}\).
\(\overrightarrow a \)và \(\overrightarrow b \) ngược hướng.
A, B, C đều sai.
Cho 2 vectơ \(\vec a\) và \(\vec b\) có \(\left| {\vec a} \right| = 4\), \(\left| {\vec b} \right| = 5\) và \(\left( {\vec a,\vec b} \right) = {120^{\rm{o}}}\).Tính \(\left| {\vec a + \vec b} \right|\)
\(\sqrt {21} \).
\(\sqrt {61} \).
\(21\).
\(61\).
Cho hai vectơ \(\vec a\) và \(\overrightarrow b \). Đẳng thức nào sau đây sai?
\(\vec a.\overrightarrow b = \frac{1}{2}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} - {{\left| {\vec a} \right|}^2} - {{\left| {\overrightarrow b } \right|}^2}} \right)\)
\(\vec a.\overrightarrow b = \frac{1}{2}\left( {{{\left| {\vec a} \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - {{\left| {\vec a - \overrightarrow b } \right|}^2}} \right)\)
\(\vec a.\overrightarrow b = \frac{1}{2}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} - {{\left| {\vec a - \overrightarrow b } \right|}^2}} \right)\)
\(\vec a.\overrightarrow b = \frac{1}{4}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} - {{\left| {\vec a - \overrightarrow b } \right|}^2}} \right)\)
Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {BC} .\)
\(\overrightarrow {AB} .\overrightarrow {BC} = {a^2}\)
\(\overrightarrow {AB} .\overrightarrow {BC} = \frac{{{a^2}\sqrt 3 }}{2}\)
\(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
\(\overrightarrow {AB} .\overrightarrow {BC} = \frac{{{a^2}}}{2}\)
Cho tam giác đều \(ABC\) có cạnh bằng \(a\) và chiều cao \(AH\). Mệnh đề nào sau đây là sai?
\(\overrightarrow {AH} .\overrightarrow {BC} = 0\)
\(\left( {\overrightarrow {AB} ,\overrightarrow {HA} } \right) = {150^0}\)
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\)
\(\overrightarrow {AC} .\overrightarrow {CB} = \frac{{{a^2}}}{2}\)
Cho tam giác \(ABC\) vuông tại \(A\) và có \(AB = c,{\rm{ }}AC = b.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} .\)
\(\overrightarrow {BA} .\overrightarrow {BC} = {b^2}\)
\(\overrightarrow {BA} .\overrightarrow {BC} = {c^2}\)
\(\overrightarrow {BA} .\overrightarrow {BC} = {b^2} + {c^2}\)
\(\overrightarrow {BA} .\overrightarrow {BC} = {b^2} - {c^2}\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình vuông \(ABCD\) cạnh \(a\). Lấy \(E\) là trung điểm của \(BC\), điểm \(F\) thoả mãn \(\overrightarrow {BF} = \frac{3}{4}\overrightarrow {BD} \) Khi đó:
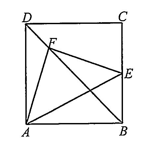
a) \(\overrightarrow {AE} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
b) \(\overrightarrow {AF} = \frac{1}{4}\overrightarrow {AB} + \frac{5}{4}\overrightarrow {AD} .\)
c) \(\overrightarrow {EF} = \frac{{ - 3}}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AD} .\)
d) Tam giác \(AEF\)vuông cân.
Cho tam giác \(ABC\) có . Gọi \(D\) là trung điểm của đoạn thẳng \(BC\). Điểm \(E\) thoả mãn \(\overrightarrow {AE} = k\overrightarrow {AC} (k \in \mathbb{R})\) (Hình). Khi đó:
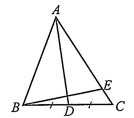
a) \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 20\)
b) \(\overrightarrow {AD} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
c) \(BC = 3\sqrt 5 \)
d) \(AD \bot BE\) khi \(k = \frac{{14}}{{15}}\).
Cho tam giác \(ABC\) đều, đường cao \(AH\). Khi đó:
a) \((\overrightarrow {AB} ,\overrightarrow {AC} ) = 30^\circ \)
b)
c) \((\overrightarrow {CA} ,\overrightarrow {BC} ) = 120^\circ \)
d) \((\overrightarrow {AH} ,\overrightarrow {BA} ) = 130^\circ \)
Cho hình thoi \(ABCD\) có cạnh bằng 2 và góc \(B\) bằng . Khi đó:
a)
b)
c) \(\overrightarrow {DA} \cdot \overrightarrow {DC} = 3\)
d) \(\overrightarrow {OB} \cdot \overrightarrow {BA} = - 3\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho tam giác \(ABC\) có \(BC = a,CA = b,AB = c\). Biết \(M\) là trung điểm của \(BC\). Tính \({\overrightarrow {AM} ^2}\)?
Cho nửa đường tròn đường kính \(AB\). Biết rằng \(AC\) và \(BD\) là hai dây thuộc nửa đường tròn cắt nhau tại \(E\). Tính \(\overrightarrow {AE} \cdot \overrightarrow {AC} + \overrightarrow {BE} \cdot \overrightarrow {BD} \) biết \(AB = 2\).
Cho hình vuông \(ABCD\), điểm \(M\) nằm trên đoạn thẳng \(AC\) sao cho \(AM = \frac{{AC}}{4}\). Gọi \(N\) là trung điểm \(CD\). Khi đó \(BMN\) là tam giác vuông cân tại đỉnh nào?
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(H\) là trung điểm của \(BC,D\) là hình chiếu của \(H\) trên \(AC,M\) là trung điểm của \(HD\). Tính \(\overrightarrow {AM} \cdot \overrightarrow {BD} \)
Cho hai điểm \(A,B\) cố định có khoảng cách bằng \(a\). Tập hợp điểm \(M\) sao cho:
\(\overrightarrow {MA} \cdot \overrightarrow {MB} = \frac{{3{a^2}}}{4}\) là đường tròn có bán kính bằng bao nhiêu?
Cho hình vuông \(ABCD\) cạnh \(a\) và số thực \(k\). Tập hợp điểm \(M\) sao cho \(\overrightarrow {MA} \cdot \overrightarrow {MC} + \overrightarrow {MB} \cdot \overrightarrow {MD} = k\) là đường tròn có bán kính bằng bao nhiêu?








