Đề kiểm tra Tích của một vecto với một số (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tam giác \(ABC\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC\). Trong các mệnh đề sau, tìm mệnh đề sai?
\(\overrightarrow {AB} = 2\overrightarrow {AM} \)
\(\overrightarrow {AC} = 2\overrightarrow {CN} \)
\(\overrightarrow {BC} = - 2\overrightarrow {NM} \)
\(\overrightarrow {CN} = - \frac{1}{2}\overrightarrow {AC} \)
Cho \(\overrightarrow a \ne \overrightarrow 0 \) và điểm \(O\). Gọi \(M,N\) lần lượt là hai điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow a \) và \(\overrightarrow {ON} = - 4\overrightarrow a \). Khi đó:
\(\overrightarrow {MN} = 7\overrightarrow a \)
\(\overrightarrow {MN} = - 5\overrightarrow a \)
\(\overrightarrow {MN} = - 7\overrightarrow a \)
\(\overrightarrow {MN} = - 5\overrightarrow a \)
Tìm giá trị của \(m\) sao cho \(\overrightarrow a = m\overrightarrow b \), biết rằng \(\overrightarrow a ,\overrightarrow b \) ngược hướng và \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 15\)
\(m = 3\)
\(m = - \frac{1}{3}\)
\(m = \frac{1}{3}\)
\(m = - 3\)
Cho tam giác \(ABC\). Gọi \(I\) là trung điểm của \(AB\). Tìm điểm \(M\) thỏa mãn hệ thức \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
\(M\) là trung điểm của \(BC\)
\(M\)là trung điểm của \(IC\)
\(M\) là trung điểm của \(IA\)
\(M\) là điểm trên cạnh \(IC\) sao cho \(IM = 2MC\)
Cho \(\Delta ABC\) có trọng tâm G. Gọi \({A_1},{B_1},{C_1}\) lần lượt là trung điểm của BC, CA, AB. Chọn đẳng thức sai.
\(\overrightarrow {G{A_1}} + \overrightarrow {G{B_1}} + \overrightarrow {G{C_1}} = \overrightarrow 0 \)
\(\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 \)
\(\overrightarrow {A{A_1}} + \overrightarrow {B{B_1}} + \overrightarrow {C{C_1}} = \overrightarrow 0 \)
\(\overrightarrow {GC} = 2\overrightarrow {G{C_1}} \)
Cho \(\Delta ABC\) với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp trọng tâm. Hệ thức nào sau đây là đúng?
\(\overrightarrow {OH} = \frac{3}{2}\overrightarrow {OG} \)
\(\overrightarrow {HO} = 3\overrightarrow {OG} \)
\(\overrightarrow {OG} = \frac{1}{2}\overrightarrow {GH} \)
\(2\overrightarrow {GO} = - 3\overrightarrow {OH} \)
Cho 4 điểm A, B, C,D. Gọi I, J lần lượt là trung điểm của AB và CD. Đẳng thức nào sau đây là sai?
\(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {IJ} \)
\(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {IJ} \)
\(\overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {IJ} \)
\(2\overrightarrow {IJ} + \overrightarrow {DB} + \overrightarrow {CA} = \overrightarrow 0 \)
Cho \(\Delta ABC\), M là một điểm trên cạnh BC. Khi đó đẳng thức nào sau đây là đúng?
\(\overrightarrow {AM} = \frac{{MC}}{{BC}}.\overrightarrow {AB} + \frac{{MB}}{{BC}}.\overrightarrow {AC} \)
\(\overrightarrow {BM} = \frac{{MA}}{{AB}}.\overrightarrow {AC} + \frac{{MB}}{{AB}}.\overrightarrow {BC} \)
\(3\overrightarrow {CM} = \frac{{MB}}{{AC}}.\overrightarrow {AB} + \frac{{MA}}{{AB}}.\overrightarrow {AC} \)
\(2\overrightarrow {AM} = \frac{{MC}}{{BC}}.\overrightarrow {AB} + \frac{{MB}}{{BC}}.\overrightarrow {AC} \)
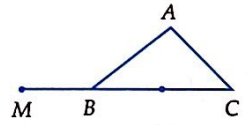
Cho \(\Delta ABC\). Trên đường thẳng BC lấy điểm M sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} \). Điểm M được vẽ đúng trong hình nào sau đây?
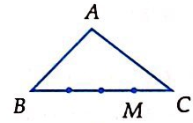
B. 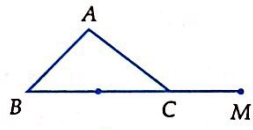
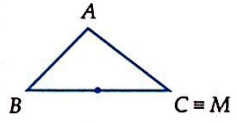
Cho \(\Delta ABC\) có G là trọng tâm. Xác định điểm M sao cho: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
Điểm M là trung điểm cạnh AC.
Điểm M là trung điểm cạnh GC.
Điểm M chia đoạn AB theo tỉ số 4.
Điểm M chia đoạn GC thỏa mãn \(\overrightarrow {GC} = 4\overrightarrow {GM} \).
Cho \(\Delta ABC\), I là trung điểm của AC. Vị trí điểm N thỏa mãn \(\overrightarrow {NA} + 2\overrightarrow {NB} = \overrightarrow {CB} \) xác định bởi hệ thức:
\(\overrightarrow {BN} = \frac{1}{3}\overrightarrow {BI} \)
\(\overrightarrow {BN} = 2\overrightarrow {BI} \)
\(\overrightarrow {BN} = \frac{2}{3}\overrightarrow {BI} \)
\(\overrightarrow {BN} = 3\overrightarrow {BI} \)
Cho 2 điểm A, B là hai số thực a, b sao cho \(a + b \ne 0\). Xét các mệnh đề:
(I) Tồn tại duy nhất một điểm M thỏa mãn \(a\overrightarrow {MA} + b\overrightarrow {MB} = \overrightarrow 0 \).
(II) \(\overrightarrow {MA} = - \frac{b}{{a + b}}\overrightarrow {AB} \).
(III) M là điểm nằm trên đường thẳng AB.
Trong các mệnh đề trên thì:
(I) và (III) tương đương nhau
(II) và (III) tương đương nhau
(I) và (II) tương đương nhau
(I), (II), (III) tương đương nhau
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác \(ABC\) có hai đường trung tuyến \(BN,CP\). Khi đó:
a) \(G\) là trọng tâm của tam giác \(ABC\), ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0\)
b) \(\overrightarrow {BA} + \overrightarrow {BC} = 3\overrightarrow {BN} \)
c) \(\overrightarrow {AB} = - \frac{2}{3} \cdot \overrightarrow {BN} - \frac{2}{3}\overrightarrow {CP} \)
d) \(\overrightarrow {BC} = - \frac{2}{3}\overrightarrow {CP} + \frac{2}{3}\overrightarrow {BN} {\rm{. }}\)
Cho hình bình hành \(ABCD\) có tâm \(O,M\) là một điểm bất kỳ. Khi đó:
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) \(\overrightarrow {AB} + 5\overrightarrow {AC} + \overrightarrow {AD} = 6\overrightarrow {AC} \)
c) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MO} \)
d) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
Cho tứ giác \(OABC\). Gọi \(M,N\) lần lượt là trung điểm của \(OB\) và \(OC\). Khi đó:
a) \(\overrightarrow {AM} = \overrightarrow {AO} + \overrightarrow {AB} \)
b) \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} \);
c) \(\overrightarrow {BN} = \frac{1}{3}\overrightarrow {OC} - \overrightarrow {OB} \);
d) \(\overrightarrow {MN} = \frac{1}{2}(\overrightarrow {OC} - \overrightarrow {OB} )\).
Cho \(\Delta ABC\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,AC\). Khi đó:
a) \[2\overrightarrow {CM} = \overrightarrow {CB} + \overrightarrow {CA} \]
b) \(\overrightarrow {AB} = - \frac{2}{3}\overrightarrow {CM} - \frac{4}{3}\overrightarrow {BN} \)
c) \(\overrightarrow {AC} = \frac{4}{3}\overrightarrow {CM} + \frac{2}{3}\overrightarrow {BN} \)
d) \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {BN} - \frac{1}{3}\overrightarrow {CM} \).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
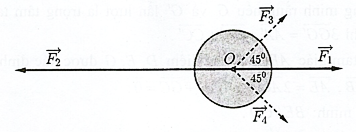
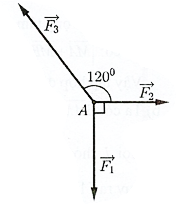
Một chất điểm A chịu tác dụng của ba lực \(\overrightarrow {{F_1},} \overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) như hình vẽ biết chất điểm \(A\) đang ở trạng thái cân bằng. Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) biết rằng lực \(\overrightarrow {{F_1}} \) có độ lớn 12N
Cho tam giác \(ABC\). Gọi \(M\) là một điểm trên cạnh \(BC\) sao cho \(MB = 2MC\). Phân tích \(\overrightarrow {AM} \) theo \(\overrightarrow {AB} ,\,\overrightarrow {AC} \).
Cho tứ giác \(ABCD\). Gọi \(I,J\) lần lượt là trung điểm của \(AC\) và \(BD\). Biết \(\overrightarrow {AB} + \overrightarrow {CD} = k\overrightarrow {IJ} \), khi đó \(k = ?\)
Cho \(\Delta ABC\) có trọng tâm \(G\). Các điểm \(D,E,F\) lần lượt là trung điểm của các cạnh \(BC,CA,AB\) và \(I\) là giao điểm của \(AD\) và \(EF\). Đặt \(\vec u = \overrightarrow {AE} ,\vec v = \overrightarrow {AF} \). Hãy phân tích các vectơ \(\overrightarrow {AI} \) theo hai vectơ \(\vec u\) và \(\vec v\).
Nếu \(G\) và \({G^\prime }\) lần lượt là trọng tâm tam giác \(ABC\) và \({A^\prime }{B^\prime }{C^\prime }\) thì \(k\overrightarrow {G{G^\prime }} = \overrightarrow {A{A^\prime }} + \overrightarrow {B{B^\prime }} + \overrightarrow {C{C^\prime }} \), khi đó \(k = ?\)
Một vật đang ở vị trí \(O\) chịu hai lực tác dụng ngược chiều nhau là \({\vec F_1}\) và \(\overrightarrow {{F_2}} \), trong đó độ lớn lực \({\vec F_2}\) lớn gấp đôi độ lớn lực \({\vec F_1}\). Người ta muốn vật dừng lại nên cần tác dụng vào vật hai lực \({\vec F_3},{\vec F_4}\) có phương hợp với lực \({\vec F_1}\) các góc 450 như hình vẽ, chúng có độ lớn bằng nhau và bằng \(20\;N\). Tìm độ lớn của mỗi lực \({\vec F_1},\overrightarrow {{F_2}} \).