Đề kiểm tra Tích của một vecto với một số (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Khẳng định nào sai?
\(1.\overrightarrow a = \overrightarrow a \)
\(k\overrightarrow a \) và \(\overrightarrow a \) cùng hướng khi \(k > 0\)
\(k\overrightarrow a \) và \(\overrightarrow a \) cùng hướng khi \(k < 0\)
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \ne \overrightarrow 0 \) cùng phương khi có một số \(k\) để \(\overrightarrow a = k\overrightarrow b \)
Trên đường thẳng \(MN\) lấy điểm \(P\) sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm \(P\) được xác định đúng trong hình vẽ nào sau đây: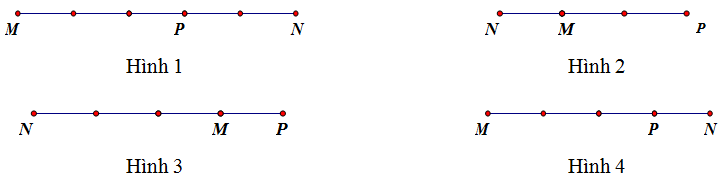
Hình 3
Hình 4
Hình 1
Hình 2
Cho ba điểm phân biệt \(A,B,C\). Nếu \(\overrightarrow {AB} = - 3\overrightarrow {AC} \) thì đẳng thức nào dưới đây đúng?
\(\overrightarrow {BC} = - 4\overrightarrow {AC} \)
\(\overrightarrow {BC} = - 2\overrightarrow {AC} \)
\(\overrightarrow {BC} = 2\overrightarrow {AC} \)
\(\overrightarrow {BC} = 4\overrightarrow {AC} \)
Cho tam giác \(ABC\). Gọi \(I\) là trung điểm của \(BC\).Khẳng định nào sau đây đúng
\(\overrightarrow {BI} = \overrightarrow {IC} \)
\(3\overrightarrow {BI} = 2\overrightarrow {IC} \)
\(\overrightarrow {BI} = \overrightarrow {2IC} \)
\(\overrightarrow {2BI} = \overrightarrow {IC} \)
Cho hai tam giác \(\Delta ABC\) và \(\Delta A'B'C'\) có trọng tâm lần lượt là G và \(G'\). Đẳng thức nào sau đây đúng?
\(\overrightarrow {A'A} + \overrightarrow {B'B} + \overrightarrow {C'C} = 3\overrightarrow {GG'} \)
\(\overrightarrow {AB'} + \overrightarrow {BC'} + \overrightarrow {CA'} = 3\overrightarrow {GG'} \)
\(\overrightarrow {AC'} + \overrightarrow {BA'} + \overrightarrow {CB'} = 3\overrightarrow {GG'} \)
\(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = 3\overrightarrow {GG'} \)
Cho 5 điểm A, B C, D, E. Đẳng thức nào sau đây là đúng?
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = 2\left( {\overrightarrow {CB} + \overrightarrow {ED} } \right)\)
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = \frac{1}{2}\left( {\overrightarrow {CB} + \overrightarrow {ED} } \right)\)
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = \frac{3}{2}\left( {\overrightarrow {CB} + \overrightarrow {ED} } \right)\)
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = \overrightarrow {CB} + \overrightarrow {ED} \)
Cho \(\Delta ABC\) và một điểm M tùy ý. Chọn hệ thức đúng?
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = \overrightarrow {AC} + 2\overrightarrow {BC} \)
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = 2\overrightarrow {AC} + \overrightarrow {BC} \)
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = 2\overrightarrow {CA} + \overrightarrow {CB} \)
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = 2\overrightarrow {CB} - \overrightarrow {CA} \)
Cho hình chữ nhật ABCD, I, K lần lượt là trung điểm của BC và CD. Chọn đẳng thức đúng.
\(\overrightarrow {AI} + \overrightarrow {AK} = 2\overrightarrow {AC} \)
\(\overrightarrow {AI} + \overrightarrow {AK} = \overrightarrow {AB} + \overrightarrow {AD} \)
\(\overrightarrow {AI} + \overrightarrow {AK} = \overrightarrow {IK} \)
\(\overrightarrow {AI} + \overrightarrow {AK} = \frac{3}{2}\overrightarrow {AC} \)
Cho hai điểm A và B. Tìm điểm I sao cho \(\overrightarrow {IA} + 2\overrightarrow {IB} = \overrightarrow 0 \).
Điểm I ngoài đoạn AB sao cho \(IB = \frac{1}{3}AB\)
Điểm I thuộc đoạn AB sao cho \(IB = \frac{1}{3}AB\)
Điểm I là trung điểm đoạn AB
Điểm I nằm khác phía với B đối với A và \(IB = \frac{1}{3}AB\).
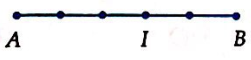
Cho đoạn thẳng AB. Hình nào sau đây biểu diễn điểm I sao cho \(\overrightarrow {AI} = - \frac{3}{5}\overrightarrow {BA} \).
A. ![]()


Trên đường thẳng MN lấy điểm P sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Hình vẽ nào sau đây xác định đúng vị trí điểm M.
![]()
B. ![]()
C. ![]()
![]()
Cho đoạn thẳng AB và điểm M là một điểm trong đoạn AB sao cho \(AM = \frac{1}{5}AB\). Tìm k để \(\overrightarrow {MA} = k\overrightarrow {MB} \).
\(k = \frac{1}{4}\)
\(k = 4\)
\(k = - \frac{1}{4}\)
\(k = - 4\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình bình hành \(ABCD\) và các điểm \(M,N,P\) thoả mãn \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN} = \frac{1}{6}\overrightarrow {AC} ,\overrightarrow {AP} = \frac{1}{4}\overrightarrow {AD} \). Khi đó:
a) \(\overrightarrow {AN} = \frac{1}{6}(\overrightarrow {AB} + \overrightarrow {AD} )\)
b) \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AD} .\)
c) \(\overrightarrow {MP} = \frac{1}{3}\overrightarrow {AD} - \frac{1}{2}\overrightarrow {AB} \)
d) Ba điểm \(M,N,P\) thẳng hàng.
Cho ngũ giác ABCDE. Các điểm M,N,P,Q,R,S theo thứ tự là trung điểm của các đoạn EA,AB,BC,CD,MP,NQ. Khi đó:
a) \(\overrightarrow {RS} = \frac{1}{2}(\overrightarrow {MN} + \overrightarrow {PQ} )\)
b) \(\overrightarrow {RS} = \frac{1}{3}\overrightarrow {ED} .\)
c) \(RS\)cắt \(ED\)
d) \(RS = \frac{1}{4}ED\)
Cho bốn điểm A,B,C,D có M,N là trung điểm của AB,CD. Khi đó:
a) \(\overrightarrow {MA} + \overrightarrow {MB} = \vec 0\)
b) \(\overrightarrow {NC} + \overrightarrow {ND} = \vec 0{\rm{. }}\)
c) \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} \)
d) \(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} {\rm{. }}\)
Cho tam giác \(ABC\) có \(G\) là trọng tâm. Gọi \(D\) là điểm đối xứng của \(B\) qua \(G,M\) là trung điểm của \(BC\). Khi đó:
a) \(\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {GD} \)
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BN} \)
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} {\rm{. }}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho \(\Delta ABC\) vuông tại \(B\) có . Gọi \(I\) là trung điểm của \(AC\). Hãy tính:\(|\overrightarrow {BA} + \overrightarrow {BC} |\)
Cho \(\Delta ABC\) vuông tại \(B\) có \(\hat A = {30^^\circ },AB = a\). Gọi \(I\) là trung điểm của \(AC\). Hãy tính:
\(|\overrightarrow {AB} + \overrightarrow {AC} |\).
Cho tứ giác \(ABCD\). Gọi \(I,J\) theo thứ tự là trung điểm của \(AB,CD\) và \(IJ = \frac{5}{4}\).
Gọi \(M,N\) theo thứ tự là trung điểm của \(BC,AC\). Tính \(|\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CI} |\)?
Cho tam giác \(ABC\) và một điểm \(M\) tùy ý, \(G\) là trọng tâm tam giác \(ABC\). Điểm \(N\) thỏa mãn \(\overrightarrow {MN} = 4\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \). Đường thẳng \(MN\) luôn qua một điểm cố định. Khi đó điểm cố định đó là điểm nào?
Cho tam giác \(ABC\) và một điểm \(M\) tùy ý không thuộc các đường thẳng \(AB,BC,AC\). Gọi \({A^\prime },{B^\prime },{C^\prime }\) theo thứ tự là các điểm đối xứng của \(M\) qua các trung điểm \(J,K,I\) của cạnh \(BC,AC,AB\).
Biết ba đường thẳng \(A{A^\prime },B{B^\prime },C{C^\prime }\) đồng quy tại một điểm (đặt điểm đó là \(N\)).
Khi đó \(MN\) luôn đi qua một điểm cố định khi \(M\) di động. Vậy điểm cố định đó là điểm nào?
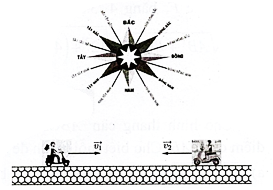
Một người đi xe máy từ Tây sang hướng Đông với vận tốc 40 km/h được biểu thị bởi vectơ \(\overrightarrow {{v_1}} \), một người khác đi xe máy từ hướng Đông sang hướng Tây với vận tốc 60 km/h được biểu thị bởi vectơ \(\overrightarrow {{v_2}} \). Hãy biểu diễn vectơ \(\overrightarrow {{v_2}} \) theo \(\overrightarrow {{v_1}} \).