Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) - Đề 5
22 câu hỏi
Cho hình hộp ABCD.A'B'C'D'. Vectơ \[\overrightarrow u = \overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} \] bằng vectơ nào dưới đây?
\(\overrightarrow {BD} \).
\(\overrightarrow {BD'} \).
\(\overrightarrow {BC} \).
\(\overrightarrow {BA'} \).
Cho tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ?
\({60^0}\).
\[{45^0}\].
\[{90^0}\].
\[{120^0}\].
Cho điểm \(M\) thỏa mãn \(\overrightarrow {OM} = 2\overrightarrow i + 3\overrightarrow j - \overrightarrow k \). Tọa độ của điểm \(M\)là
\(\left( {2;3;1} \right)\).
\(\left( { - 2; - 3;1} \right)\).
\(\left( {2; - 1;3} \right)\).
\(\left( {2;3; - 1} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho vectơ \[\overrightarrow u = 2\overrightarrow i - \frac{1}{2}\overrightarrow j + 4\overrightarrow k \]. Tọa độ của vectơ \[\overrightarrow u \] là:
\(\left( {2; - \frac{1}{2};4} \right)\).
\(\left( {2;\frac{1}{2};4} \right)\).
\(\left( {2;1;4} \right)\).
\(\left( {\frac{1}{2}; - 2;\frac{1}{4}} \right)\).
Trong không gian với hệ tọa độ Oxyz , cho hai véctơ ![]() và
và ![]() . Tìm tọa độ của véc tơ
. Tìm tọa độ của véc tơ ![]() .
.
\[\overrightarrow a \left( { - 8;9; - 1} \right)\].
\[\overrightarrow a \left( {8;9; - 1} \right)\].
\[\overrightarrow a \left( { - 8; - 9;1} \right)\].
\[\overrightarrow a \left( { - 8; - 9; - 1} \right)\].
Trong không gian với hệ toạ độ Oxyz, cho vectơ \(\overrightarrow a = \left( { - 1;4;2} \right)\). Toạ độ của vectơ \( - 2\overrightarrow a \) là
\(\left( { - 2;8;4} \right)\).
\(\left( {2; - 8; - 4} \right)\).
\(\left( { - 2; - 8; - 4} \right)\).
\(\left( {2;8;4} \right)\).
Trong không gian với hệ tọa độ Oxyz, độ dài của vectơ \(\overrightarrow u = \left( {2; - 1;2} \right)\) là
\(\sqrt 7 \).
\(3\).
\(9\).
\(2\).
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow u = \left( { - 2;1;5} \right)\) và \(\overrightarrow v = \left( {0; - 3;1} \right)\). Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là
\(\sqrt {30} .\sqrt {10} \).
\( - \sqrt {30} .\sqrt {10} \).
\(2\).
\( - 2\).
Trong không gian Oxyz cho hai điểm \[A\left( {2; - 4;3} \right),\,\,B\left( {2;2;7} \right)\]. Trung điểm của \(AB\) có toạ độ là
\(\left( {2;6;4} \right)\)
\[\left( {1;3;2} \right)\]
\(\left( {4; - 2;10} \right)\).
\[\left( {2; - 1;5} \right)\]
Cho hai điểm \(A\left( {2\,;\,3\,;\, - 4} \right)\) và \(B\left( {0\,;\,1\,;\,6} \right)\). Trung điểm \(M\) của đoạn thẳng \(AB\) có tọa độ là:
\(M\)\(\left( { - 2\,;\, - 2\,;\,10} \right)\).
\(M\)\(\left( {1\,;\,2\,;\,2} \right)\).
\(M\)\(\left( {1\,;\,2\,;\,1} \right)\).
\(M\)\(\left( {2\,;\,2\,;\, - 10} \right)\).
Cho tam giác MNP có \(M\left( {1;1} \right),N\left( { - 1;0} \right),P\left( {3; - 7} \right).\)Trọng tâm \(G\) của tam giác MNP có tọa độ là
\(\left( {1; - 2} \right).\)
\(\left( { - 1;2} \right).\)
\(\left( {1;2} \right).\)
\(\left( {3; - 6} \right).\)
Trong không gian, xét hệ tọa độ Oxyz có gốc \(O\) trùng với vị trí của một giàn khoan trên biển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục \[Oy\]hướng về phía nam và trục \(Oz\) hướng thẳng đứng lên trời (H.2.52). Đơn vị đo trong không gian \[Oxyz\] lấy theo kilômét. Một chiếc ra đa đặt tại giàn khoan và một chiếc tàu thám hiểm có tọa độ là \(\left( {30;25; - 15} \right)\). Khoảng cách theo đơn vị kilômét từ chiếc ra đa và một chiếc tàu thám hiểm. ( Kết quả làm tròn lấy một chữ số thập phân)
\(41,8km\).
\(31,8km\).
\(41,9km\).
\(31,9km\).
PHẦN 2. CÂU HỎI ĐÚNG SAI (4 CÂU)
Cho hình chóp ABCD có AB,AC,AD đôi một vuông góc, cạnh AB = AC = a ,\[M\] là trung điểm của \[CB\],\[H\] là trung điểm của \[MD\]. Các mệnh đề dưới đây đúng hay sai?
a) \(\overrightarrow {DM} = \frac{{\overrightarrow {BD} + \overrightarrow {{\rm{CD}}} }}{{ - 2}}\)
b) \(\overrightarrow {AH} = \frac{{\overrightarrow {AD} }}{2} + \frac{{\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} }}{4}\)
c)\(\overrightarrow {AB} .\overrightarrow {AH} = \frac{{{a^2}}}{4}\).
d) Góc giữa vectơ \[\overrightarrow {AH} \] và \(\overrightarrow {BC} \) bằng \(60^\circ \).
Trong không gian hệ tọa độ Oxyz cho hai điểm \(M( - 4;3; - 1)\)và \(N(2; - 1; - 3)\)
a) Tìm tọa độ vectơ \(\overrightarrow {OM} ( - 4;3; - 1)\)
b) Cho vectơ \(\overrightarrow v = \overrightarrow i + \overrightarrow {2j} - 3\overrightarrow k \)và \(\overrightarrow {AM} = \overrightarrow v \). Tọa độ vủa điểm \[A\] là: \(A(5;1;2)\)
c) Gọi \(G\) là trọng tâm của \(\Delta OMN\). Tọa độ hình chiếu của \(G\) trên \(Oxy\) là \(\left( {0;\,0;\, - \frac{4}{3}} \right)\)
d) I là trung điểm của đoạn \[MN\]. Tọa độ của vectơ \[\overrightarrow w = 3\overrightarrow i + 2\overrightarrow {ON} - \frac{1}{2}\overrightarrow {OI} \]là \[\left( {\frac{9}{2};\frac{{ - 5}}{2}; - 7} \right)\]
Trong không gian Oxyz, cho \(\Delta ABC\)với \(A\left( {1\,;\,2\,;\,3} \right)\), \(B\left( {4\,;\,5\,;\,6} \right)\), \(C\left( {2\,;\,7\,;\,4} \right)\)
a) Tọa độ trung điểm của cạnh \(AB\) là \(M\left( {\frac{5}{2}\,;\,\frac{7}{2}\,;\,\frac{9}{2}} \right)\).
b) Tọa độ trọng tâm \(G\) của \(\Delta ABC\) là \(G\left( {\frac{7}{3};\,\frac{{14}}{3}\,;\,\frac{{13}}{3}} \right)\).
c) Tích vô hướng của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là 31.
d) Chu vi và diện tích của \(\Delta ABC\) lần lượt là \(8\sqrt 3 \) và \(6\sqrt 2 \,\).
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm điểm \(A\left( {0\,;\,\, - 2\,;\,\,1} \right);\,\)\(B\left( {1\,;\,\,0\,;\,\, - 2} \right)\); \(C\left( {\,3\,;\,\,1\,;\,\, - 2} \right)\) và \(\,D\left( { - 2;\, - 2;\, - 1} \right)\).
a) Ba điểm \(A,\,B,D\) thẳng hàng
b) Tam giác \[ACD\] là tam giác vuông tại \(A\).
c) Góc giữa hai véctơ\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là góc tù.
d) Bốn điểm \(A,\,B,\,C,\,D\) không đồng phẳng.
PHẦN 3. CÂU HỎI TRẢ LỜI NGẮN (6 CÂU)
(1,0 điểm) . Cho tứ diện ABCD có AB = AC = AD = a \[\widehat {BAC} = \widehat {BAD} = 60^\circ ,\,\] \[\widehat {CAD} = 90^\circ \]. Gọi \(I\) là điểm trên cạnh \(AB\) sao cho \(AI = 3IB\) và \(J\) là trung điểm của \(CD\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \)?
Trong không gian với hệ toạ độ Oxyz, cho hình hộp ABCD.A'B'C'D' có \[A\left( {0;\,\,0;\,\,0} \right)\],\[B\left( {3;\,\,0;\,\,0} \right)\],\[D\left( {0;\,\,3;\,\,0} \right)\],\[D'\left( {0;\,\,3;\,\, - 3} \right)\]. Tìm tọa độ các đỉnh \(C\) và \(A'\) của hình hộp?
Trong không gian Oxyz, cho tứ diện ABCD có \(A(0\,;\,1\,;\, - 1)\), \(B(1\,;\,1\,;\,2)\), \(C(1\,;\, - 1\,;\,0)\), \(D(0\,;\,0\,;\,1)\). Tìm một vectơ khác \(\overrightarrow 0 \) vuông góc với cả hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \)?
Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm \[A\left( {800;500;7} \right)\] đến điểm \[B\left( {940;550;9} \right)\] trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là \(C(x;y;z)\). Tính \(x + y + z\).
Một tấm gỗ tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không giãn xuất phát từ điểm \(O\) trên trần nhà và lần lượt buộc vào ba điểm \(A,B,C\) trên tấm gỗ tròn sao cho các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) lần lượt trên mỗi dây \(OA,OB,OC\) đôi một vuông góc với nhau và có độ lớn \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 10\left( N \right)\) (xem hình vẽ).
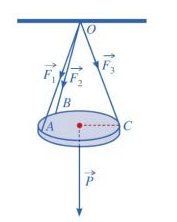
Tính trọng lượng \(P\) của tấm gỗ tròn đó.
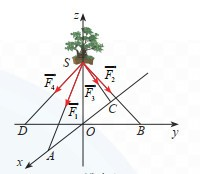
(1,0 điểm) Một chậu cây được đặt trên một giá đỡ có bốn chân với điểm đặt \(S\left( {0;0;30} \right)\) và các điểm chạm mặt đất của bốn chân lần lượt là \(A\left( {30;0;0} \right),B\left( {0;20;0} \right),C\left( { - 20;0;0} \right),D\left( {0; - 20;0} \right)\) (đơn vị cm). Cho biết trọng lực tác dụng lên chậu cây có độ lớn \(60N\)và được phân bố thành bốn lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \) có độ lớn bằng nhau như hình vẽ. Tính \(\left| {\overrightarrow {{F_1}} + 2\overrightarrow {{F_2}} + 3\overrightarrow {{F_3}} + 4\overrightarrow {{F_4}} } \right|\) (kết quả làm tròn đến hàng đơn vị)