Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỈ chọn một phương án.
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây đúng?
\[\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AB} \].
\[\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \].
\[\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AC} + \overrightarrow {AD'} \].
\[\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AD'} + \overrightarrow {AA'} \].
Nếu một vật có khối lượng \[m(kg)\] thì lực hấp dẫn \[\overrightarrow P \]của trái đất tác dụng lên vật được xác định theo công thức \[\overrightarrow p = m\,\overrightarrow g \], trong đó \[\overrightarrow g \] là gia tốc rơi tự do có độ lớn \[g = 9,8\left( {m/{s^2}} \right)\]. Độ lớn của lực trái đát tác dụng lên một quả lê có khối lượng \[105g\]là
\[102,9N\].
\[1029N.\].
\[1,029N\].
\[10,29N\].
Cho biết máy bay \[A\]đang bay với vận tốc \[\overrightarrow u = \left( {300;200;400} \right)\]( đơn vị:\[km/h)\]Máy bay \[B\]ngược hướng và có tốc độ gấp 2 lần tốc độ của máy bay \[A\]. Tọa độ vectơ vận tốc \[\overrightarrow v \]của máy bay \[B\]là
\[\overrightarrow v = \left( {600;400;800} \right)\].
\[\overrightarrow v = \left( {150;100;200} \right)\].
\[\overrightarrow v = \left( { - 600; - 400; - 800} \right)\].
\[\overrightarrow v = \left( { - 150; - 100; - 200} \right)\].
Cho hai điểm \[A\left( { - 3;2; - 1} \right),\,B\left( { - 1;0;5} \right)\]. Tọa độ trung điểm \[I\] của đoạn thẳng \[AB\] là
\[I\left( { - 1;1;2} \right)\]
\[I\left( {2;1; - 2} \right)\].
\[I\left( { - 2; - 1;2} \right)\]
\[I\left( { - 2;1;2} \right)\].
Trong không gian Oxyz, biết \(\overrightarrow {OM} = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k \). Toạ độ của điểm \(M\) là
\(\left( { - 2;3; - 1} \right)\).
\(\left( {2; - 3;1} \right)\).
\(\left( { - 3;2;1} \right)\).
\(\left( {2;1; - 3} \right)\).
Trong không gian Oxyz, cho hai điểm \(A\left( { - 2;2;1} \right),B\left( {0;1;3} \right)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là
\(\overrightarrow {AB} = \left( {2; - 1;2} \right)\).
\(\overrightarrow {AB} = \left( { - 2;3;4} \right)\).
\(\overrightarrow {AB} = \left( { - 2;1; - 2} \right)\).
\(\overrightarrow {AB} = \left( { - 2;2;3} \right)\).
Cho tứ diện đều ABCD có cạnh bằng \(2\). Tính \(\overrightarrow {AB} .\overrightarrow {CD} \).
\(\overrightarrow {AB} .\overrightarrow {CD} = - 4\).
\(\overrightarrow {AB} .\overrightarrow {CD} = 2\).
\(\overrightarrow {AB} .\overrightarrow {CD} = 1\).
\(\overrightarrow {AB} .\overrightarrow {CD} = 0\).
Trong không gian Oxyz, cho hai điểm \(M\left( { - 5;2;3} \right),I\left( {2;3;1} \right)\). Gọi \(N\) là điểm đối xứng với \(M\) qua \(I\). Tính độ dài đoạn \(ON\).
\(ON = 6\sqrt 2 \).
\(ON = 5\sqrt 2 \).
\(ON = 7\sqrt 2 \).
\(ON = 3\sqrt 2 \).
Trong không gian với hệ trục tọa độ Oxyz, cho hai vec tơ \(\overrightarrow a \left( {1;\,\, - 2;\,\,0} \right)\) và \(\overrightarrow b \left( { - 2;\,\,3;\,\,1} \right)\). Cho các mệnh đề sau.
a) \(\overrightarrow a .\overrightarrow b = - 8\).
b) \(2\overrightarrow a = \left( {2;\,\, - 4;\,\,1} \right)\).
c) \(\overrightarrow a + \overrightarrow b = \left( { - 1;\,\,0;\,\, - 1} \right)\).
d) \(\left| {\overrightarrow b } \right| = 14\).
Số mệnh đề ĐÚNG là:
1.
3
2.
4.
Trong không gian với hệ trục tọa độ Oxyz cho \(\overrightarrow a = \left( {1; - 2;3} \right)\) và \(\overrightarrow b = \left( {2; - 1; - 1} \right)\).Cho các mệnh đề sau. Mệnh đề nào là mệnh đề SAI?
Vec tơ cùng vuông góc với vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) có tọa độ bằng \(\left( { - 5; - 7; - 3} \right)\).
Vectơ \(\overrightarrow a \) không cùng phương với vectơ \(\overrightarrow b \).
Vectơ \(\overrightarrow a \) không vuông góc với vectơ \(\overrightarrow b \).
\(\left| {\overrightarrow a } \right| = 14\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm \(O\). Trong các mệnh đề sau mệnh đề nào là mệnh đề SAI?
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \).
\(\overrightarrow {SA} - \overrightarrow {SB} + \overrightarrow {SC} - \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
Một chiếc đèn chùm treo có khối lượng m = 5kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA,SB,SC,SD sao cho S.ABCD là hình chóp tứ giác đều có (Hình).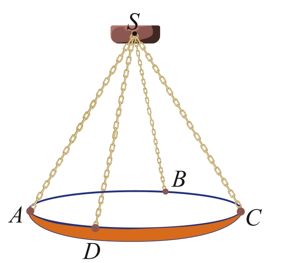
Biết \(\vec P = m\vec g\) trong đó \(\vec g\) là vectơ gia tốc rơi tự do có độ lớn \(10\;m/{s^2}\), \(\vec P\) là trọng lực tác động vật có đơn bị là \(N\), \(m\) là khối lượng của vật có đơn vị \(kg\). Cho các kết luận dưới đây.
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vec tơ đồng phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|.\)
c) Độ lớn của trọng lực \(\vec P\) tác động lên chiếc đèn chùm bằng \(50\;N.\)
d) Độ lớn của lực căng cho mỗi sợi xích bằng \(\frac{{25\sqrt 3 }}{6}\;N.\)
Số kết luận ĐÚNG là:
1.
2.
3.
0.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ tọa độ Oxyz,cho hai vectơ \(\overrightarrow a = \left( {1;2; - 2} \right)\)và \(\overrightarrow b = \left( { - 1; - 1;0} \right)\). Các mệnh đề dưới đây đúng hay sai ?
a)\(\left| {\overrightarrow a } \right| = 9\)
b)\(\overrightarrow a + \overrightarrow b = \left( {0;1; - 2} \right)\)
c)\(\overrightarrow a \) và \(\overrightarrow b \) cùng phương.
d)\(\left( {\overrightarrow a ,\overrightarrow b } \right) = 135^\circ \)
Cho 4 điểm \(A(1;2;0);B(5;1;4);C(7; - 2; - 2);D(3;m;2)\)
a) Độ dài đoạn \(AB\) lớn hơn độ dài đoạn \(AC\).
b) \(m = \frac{3}{2}\) thì \(D\) là trung điểm của \(AB\).
c) \(m = 5\) thì \(AB \bot AD\).
d) \(m = - 1\) thì \(AB\)//\(CD\).
Trong không gian Oxyz, cho các điểm \(A\left( {8;9;2} \right)\), \(B\left( {3;5;1} \right)\) và \(C\left( {11;10;4} \right)\).
a) Điểm \(D\) thỏa mãn \(ABCD\) là hình bình hành có tọa độ là \(D\left( {6;6;3} \right)\)
b) Độ dài trung tuyến \(AM\) bằng \(\frac{{\sqrt {14} }}{2}\).
c) \(\widehat {BAC} = {30^ \circ }\).
d) Điểm \(N\) thuộc mp\(\left( {Oxy} \right)\) sao cho ba điểm \(A\), \(B\), \(N\) thẳng hàng có tọa độ là \(N\left( { - 2;1;0} \right)\).
Cho hình hộp ABCD.A'B'C'D'; Các điểm \(M,\,N\)lần lượt thuộc các đường thẳng CA và \(DC'\)sao cho \(\overrightarrow {MC} = m\overrightarrow {MA} ;\,\,\overrightarrow {ND} = m\overrightarrow {NC'} \). Đặt \[\overrightarrow {BA} = \overrightarrow a \,;\,\,\overrightarrow {BB'} = \overrightarrow b ;\,\overrightarrow {BC} = \overrightarrow c \]
a)\(\overrightarrow {BD'} = \overrightarrow a + \overrightarrow b - \overrightarrow c \).
b)\(\overrightarrow {BM} = \frac{{\overrightarrow c - m\overrightarrow a }}{{1 - m}}\).
c) \(\overrightarrow {BN} = \frac{1}{{1 - m}}\overrightarrow a - \frac{m}{{1 - m}}\overrightarrow b + \overrightarrow c \).
d) \(m = \frac{1}{2}\) thì \(MN\)//\(BD'\)
Phần III. Câu hỏi trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\left( {1;\,0;\,3} \right)\), \(B\left( {2;\,3;\, - 4} \right)\), \(C\left( { - 3;\,1;\,2} \right)\). Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.
Trong không gian với hệ tọa độ Oxyz, cho hình vuông . Biết đỉnh \(A\) thuộc mặt phẳng \(\left( {Oxy} \right)\) và có tọa độ là những số nguyên, khi đó \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right|\) bằng:
Trong không gian \[{\rm{O}}xyz\] cho hai vec tơ \[\overrightarrow a = (1; - 2;0),\,\,\overrightarrow b = (1;3; - 2)\]. Góc giữa hai vec tơ \[\overrightarrow a \] và \[\,\,\overrightarrow b \] bằng bao nhiêu ( tính theo độ làm tròn đến hàng phần chục)
Trong một phòng học được thiết kế dạng hình hộp chữ nhật, với chiều dài \[8m\], chiều rộng \[6m\] và chiều cao \[3m\]. Hai bạn An và Bình làm nhiệm vụ trực nhật, mạng nhện cần quét ở góc ngoài cùng trên trần nhà, An bảo không nên đứng ngay vị trí đó ở nền nhà quét vì sẽ bụi rơi xuông người mình, An lại đố bạn Bình ‘nếu mình đứng ở giữa nhà quét thì mình phải kéo chối quét nhà dài ra mấy mét ( làm tròn đến hàng phần trăm) để quét được vị trí mạng nhên, biết An cầm chổi cao \[1,5m\]’. Bình trả lời đứng vị trí đó chổi dài \[5m\] cũng không tới. Hỏi Bình đã tính được bao nhiêu?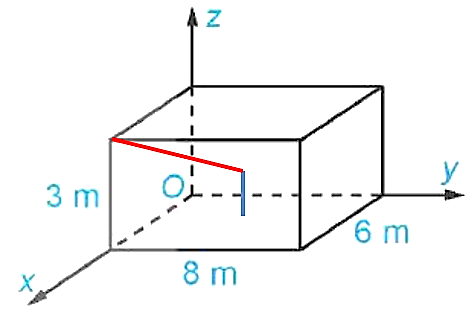
Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng \(\left( {Oxy} \right)\)là mặt nước, trục \(Oz\) hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước \(2m\), cách mặt phẳng \(\left( {Oxz} \right),\,\left( {Oyz} \right)\) lần lượt là \(3m\) và \(1m\) phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước \(50\,cm\), cách mặt phẳng \(\left( {Oxz} \right),\,\left( {Oyz} \right)\) lần lượt là \(1m\) và \(1,5\,m\)Tìm tọa độ điểm \(B\) lúc chim bói cá vừa tiếp xúc với mặt nước.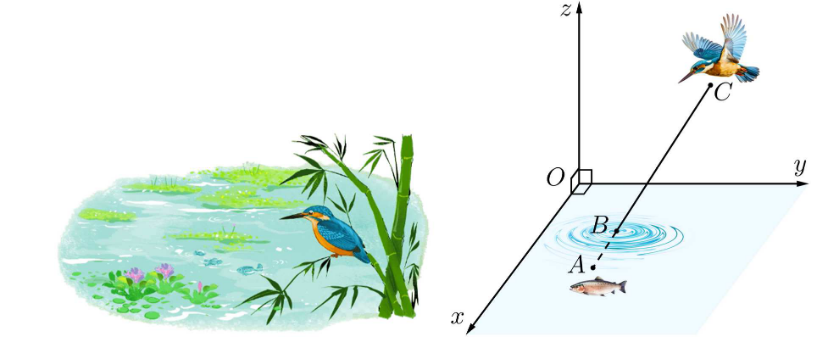
Một căn phòng dạng hình hộp chữ nhật với chiều dài \(8m\), rộng\(6m\)và cao\(4m\)có hai chiếc quạt treo tường. Chiếc quạt A treo chính giữa bức tường \(8m\)và cách trần\(1m\), chiếc quạt B treo chính giữa bức tường \(6m\)và cách trần \(1,5m\). Hỏi khoảng cách giữa hai chiếc quạt AB cách nhau bao nhiêu m ( làm tròn đến hàng phần nghìn)





