Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) - Đề 1
22 câu hỏi
Cho tứ diện \[ABCD\]. Gọi \[G\] là trọng tâm tam giác \[BCD\] và điểm \[M\] thuộc cạnh \[AB\] sao cho \[AM = 2BM\]. Đẳng thức nào sau đây là đúng?
\(\overrightarrow {MG} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
\(\overrightarrow {MG} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AD} \).
\(\overrightarrow {MG} = - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AD} \).
\(\overrightarrow {MG} = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AD} \).
Cho hình lập phương \[ABCD.EFGH\]. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và\(\overrightarrow {EG} \)?
\({60^0}\).
\[{45^0}\].
\[{90^0}\].
\[{120^0}\].
Trong không gian với hệ tọa độ \[Oxyz\], cho điểm \(A\left( {2;3; - 2} \right)\). Gọi \({A_1}\) là hình chiếu vuông góc của điểm\(A\)lên mặt phẳng \(\left( {Oyz} \right)\). Khi đó tọa độ của điểm \({A_1}\) là
\(\left( {2;3;0} \right)\).
\(\left( {2;0;0} \right)\).
\(\left( { - 2;3; - 2} \right)\).
\(\left( {0;3; - 2} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho vectơ \[\overrightarrow a = \left( {2;\frac{1}{3}; - 5} \right)\] và điểm \(M\left( {2;3;4} \right)\). Tọa độ điểm \(N\) thỏa mãn \(\overrightarrow {MN} = \vec a\) là:
\(\left( {2;\frac{5}{3}; - \frac{1}{2}} \right)\).
\(\left( {0;\frac{8}{3};9} \right)\).
\(\left( {4;\frac{{10}}{3}; - 1} \right)\).
\[\left( {0; - \frac{8}{3}; - 9} \right)\].
Trong không gian tọa độ Oxyz, cho các vectơ ![]() và
và ![]() . Toạ độ của vectơ
. Toạ độ của vectơ ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ toạ độ Oxyz, cho điểm \(M\left( {4;1; - 2} \right)\) và vectơ \(\overrightarrow u = \left( {4; - 2;6} \right).\)Tìm toạ độ điểm \(N\) biết rằng \(\overrightarrow {MN} = - \frac{1}{2}\overrightarrow u \).
\(\left( {3;3;3} \right)\).
\(\left( {3; - 3;3} \right)\).
\(\left( { - 3;3;3} \right)\).
\(\left( { - 3; - 3;3} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {2; - 1;4} \right),B\left( {5;3; - 8} \right)\). Độ dài của vectơ \(\overrightarrow {AB} \) là
\(5\).
\(8\).
\(9\).
\(13\).
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow a = \left( {1;\, - 2;\, - 3} \right)\), \(\overrightarrow b = \left( { - 2;\,m - 1;\,2} \right)\). Tìm tham số \(m\) để vectơ \(\overrightarrow a \) vuông góc với vectơ \(\overrightarrow b \)
\(m = - 3\).
\(m = 1\).
\(m = 5\).
\(m = 0\).
Trong không gian Oxyz, cho \(A\left( {4\,;\,0\,;\,0} \right)\), \(B\left( {0\,;2\,;\,0} \right)\). Tâm đường tròn ngoại tiếp tam giác\(OAB\)
\(I\left( {2\,; - 1\,;\,0} \right)\).
\(I\left( {\frac{4}{3}\,\,;\,\frac{2}{3}\,\,;\,0} \right)\).
\(I\left( { - 2\,;1\,;\,0} \right)\).
\(I\left( {2\,;1\,;\,0} \right)\).
Cho hai điểm \(A\left( {1\,;\,2\,;\,3} \right)\) và \(B\left( {3\,;\,0\,;\, - 5} \right)\). Gọi \(M\) là điểm đối xứng của \(A\) qua \(B\). Tọa độ của điểm \(M\) là:
\(\left( {2\,;\, - 2\,;\, - 8} \right)\).
\(\left( {5\,;\, - 2\,;\, - 13} \right)\).
\(\left( {2\,;\,1\,;\, - 1} \right)\).
\(\left( {7\,;\,2\,;\, - 7} \right)\).
Cho tam giác MNP có \(M\left( { - 1;3} \right),N\left( {2;2} \right),P\left( { - 1;1} \right).\)Biết \(N\) là trọng tâm của tam giác MPQ, điểm \(Q\)có tọa độ là
\(\left( {8;2} \right).\)
\(\left( {4; - 2} \right).\)
\(\left( {2;0} \right).\)
\(\left( {0; - 2} \right).\)
Một chiếc máy ảnh được đặt trên giá đỡ ba chân với điểm đặt \(E\left( {0;0;8} \right)\) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \({A_1}\left( {0;1;0} \right)\),\({A_2}\left( {\frac{{\sqrt 3 }}{2};\frac{{ - 1}}{2};0} \right)\), \({A_3}\left( {\frac{{ - \sqrt 3 }}{2};\frac{{ - 1}}{2};0} \right)\).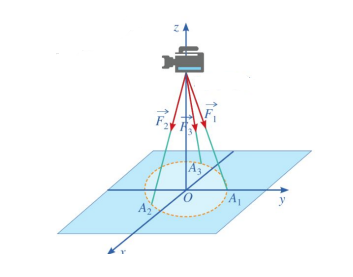
Biết rằng trọng lượng của chiếc máy là 240N. Tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow {{F_1}} \) là:
\(\overrightarrow {{F_1}} = \left( {0;10; - 80} \right)\).
\(\overrightarrow {{F_1}} = \left( {0;10;80} \right)\).
\(\overrightarrow {{F_1}} = \left( {0; - 10; - 80} \right)\).
\(\overrightarrow {{F_1}} = \left( {10;0; - 80} \right)\).
PHẦN 2. CÂU HỎI DẠNG ĐÚNG – SAI (4 CÂU)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Trên các cạnh \[CD\] và \[BB'\] ta lần lượt lấy các điểm M và N sao cho \[DM = BN = x\] với \[0 \le x \le a\]. Các mệnh đề dưới đây đúng hay sai?
a) \(\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {A{\rm{D}}} \)
b) Gọi \[K\] là trung điểm \(AD\) khi đó \(\overrightarrow {C'K} = \overrightarrow {C'C} + \overrightarrow {C'D'} + \frac{1}{2}\overrightarrow {C'B'} \).
c) \(\overrightarrow {AB} .\overrightarrow {B'D'} = {a^2}\).
d) Góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng \(60^\circ \).
Trong không gian với hệ tọa độ \(Oxyz,\)cho hình bình hành \(ABCD\) có \(A\left( { - 3;4;2} \right)\), \(B\left( { - 5;6;2} \right)\), \(C\left( { - 10;17; - 7} \right)\).
a) Tọa độ trung điểm của \(AB\) là \(I\left( { - 4;5;2} \right)\).
b) Tọa độ trọng tâm của tam giác \(ABC\) là \(G\left( { - 6;9; - 1} \right)\).
c) \(\overrightarrow {AB} .\overrightarrow {AD} = 10\).
d) Tọa độ trực tâm của tam giác \(ABD\) là \(H\left( { - 5;12;4} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\left( {2;\,1;\, - 1} \right)\), \(B\left( {3;\,1;\,0} \right)\), \(C\left( { - 1;\,1;\,3} \right)\). Các mệnh đề sau đúng hay sai?
a) Ba điểm \(A,\,B,\,C\)không thẳng hàng.
b) Ba điểm \(A,\,B,\,D\left( {4;1;1} \right)\)thẳng hàng.
c) Góc \(\widehat {ABC} = 45^\circ \).
d) \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0; - 7;0} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho \[A\left( {1;1;2} \right)\], \[B\left( {3; - 1;2} \right)\] và \[C\left( {2;0;1} \right)\].
a) Ba điểm \[A\], \[B\], \[C\]không thẳng hàng.
b) Điểm \[M\left( {a;b;3} \right)\] thõa mãn ba điểm \[A\], \[C\], \[M\] thẳng hàng thì \[a + b = 2\] .
c) Gọi \[\alpha \] là góc tạo bởi hai véc-tơ \[\overrightarrow {AB} \],\[\overrightarrow {BC} \] thì \[\cos \alpha = - 1\].
d) Gọi điểm \[M\left( {a;b;3} \right)\] thõa mãn ba điểm \[A\], \[B\], \[M\] thẳng hàng. Khi đó tích có hướng của hai véc-tơ \[\overrightarrow {AB} \] và \[\overrightarrow {AM} \] là \[\left( {1;1;2} \right)\] .
PHẦN 3. CÂU HỎI TRẢ LỜI NGẮN (6 CÂU)
(1,0 điểm) Cho hình chóp S.ABC có \[SA = SB = SC = AB = AC = a\], \[BC = a\sqrt 2 \]. Tính góc giữa hai véc tơ \[\overrightarrow {AB} \] và \[\overrightarrow {SC} \].
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có \(A\left( {1;\,0;\,1} \right)\), \(B\left( {2;\,1;\,2} \right)\), \(D\left( {1;\, - 1;\,1} \right)\), \(C'\left( {4;\,5;\, - 5} \right)\). Tính tọa độ đỉnh \(A'\) của hình hộp?
Cho hình hộp ABCD.A'B'C'D'. Biết \(A\left( {1;0;1} \right)\),\(B\left( {2;1;2} \right)\), \(D\left( {1; - 1;1} \right)\), \(C'\left( {4;5; - 5} \right)\). Tìm một vectơ khác \(\overrightarrow 0 \) vuông góc với với cả hai vectơ \(\overrightarrow {CC'} \) và \(\overrightarrow {C'D'} \).
Trong một căn phòng dạng hình hộp chữ nhật với chiều dài \(8m\), rộng \(6m\) và cao \(4m\)có \(2\)cây quạt treo tường. Cây quạt \(A\)treo chính gữa bức tường \(8m\)và cách trần \(1m\), cây quạt \(B\) treo chính giữa bức tường \(6m\)và cách trần \(1,5m\). Chọn hệ trục tọa độ \(Oxyz\)như hình vẽ bên dưới ( đơn vị: mét). Hãy xác định tọa độ của \(\overrightarrow {AB} \).

Một chi tiết trong bộ trang sức có hình bát diện đều, được gắn hệ trục tọa độ Oxyz như hình vẽ. Các hình chóp S.ABCD và I.ABCD là các hình chóp tứ giác đều cạnh \(1\,{\rm{cm}}\).
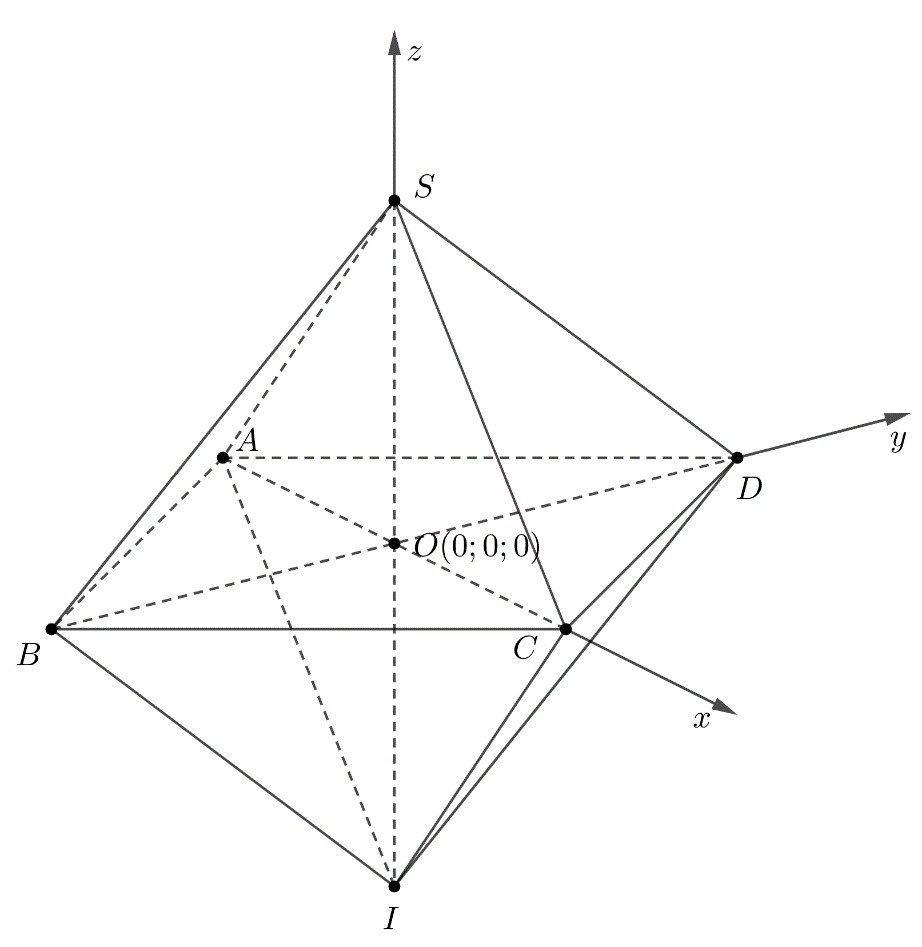
a) Tính tổng hoành độ các đỉnh \(S,A,B,C,D,I\).
b) Tính số đo góc nhị diện \[\left[ {S;CD;I} \right]\] theo đơn vị độ, làm tròn đến hàng đơn vị.
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng \(\left( {ABCD} \right)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp \(EA, EB, EC\) và \(ED\) có độ dài bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc bằng \(60^\circ \) (hình minh họa). Chiếc cần cẩu đang kéo khung sắt lên theo phương thẳng đứng.
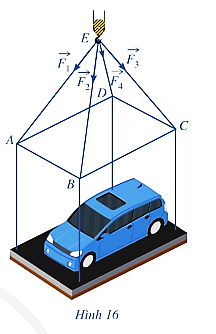
Biết rằng các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \) đều có cường độ là \(4,7{\rm{\;kN}}\) và trọng lượng của khung sắt là \(3{\rm{\;kN}}\). Tính trọng lượng lớn nhất của chiếc xe ô tô (làm tròn đến hàng phần chục)?





