Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) - Đề 2

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương ABCD.A'B'C'D'. Chất điểm chịu tác động bởi ba lực \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) lần lượt cùng hướng với \(\overrightarrow {AD} ,\overrightarrow {AB} \) và \(\overrightarrow {AC'} \) như hình vẽ. Độ lớn của các lực \(\overrightarrow a ,\overrightarrow b \)và \(\overrightarrow c \) tương ứng là \(10{\rm N},\,\,10{\rm N}\) và \(10\sqrt 3 {\rm N}.\)

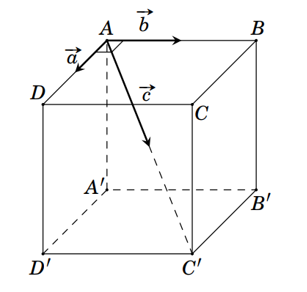
Xét tính đúng - sai của các mệnh đề sau đây:

A. \(\overrightarrow a  + \overrightarrow b  = \overrightarrow c \).                                                            

B. \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 20\left( {\rm N} \right)\).

C. \(\left| {\overrightarrow a  + \overrightarrow c } \right| = \left| {\overrightarrow b  + \overrightarrow c } \right|\).                                                      

D. \(\left| {\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right| = 30\left( {\rm N} \right)\)

(làm tròn kết quả đến hàng phần mười).

Trong không gian Oxyz, cho ba điểm\(A\left( {2;3;1} \right)\), \(B\left( { - 1;2;0} \right)\),\(C\left( {1;1; - 2} \right)\) . Phát biêủ dưới đây đúng hay sai

a) \(\overrightarrow {OA}  = 2\overrightarrow i  + 3\overrightarrow j  + \overrightarrow k \)

b) \(\overrightarrow {AB}  = \left( {3;\,\, - 1;\,\, - 1} \right)\)

c) Gọi \(D\)là điểm sao cho \(ABCD\)là hình bình hành. Khi đó \(D\left( {4;\,\,2;\,\, - 1} \right)\)\(\)

d) \(H\) là trực tâm tam giác \(ABC\), khi đó, độ dài đoạn \(OH\) bằng \[\frac{{\sqrt {870} }}{{15}}.\]

Các mệnh đề sau đúng hay sai?

a) Trong không gian với hệ trục tọa độ Oxyz, cho 2 vectơ \(\vec u = m\vec i + 2\vec j - 3\vec k,\,\,\,\vec v = m\vec j + 2\vec i + 4\vec k\). Biết rằng \(\vec u.\vec v = 8\), khi đó giá trị của \(m\) bằng 5.

b) Trong không gian \(Oxyz\), cho hai véctơ \[\overrightarrow u  = \left( {1;\, - 2;\,1} \right)\] và \(\overrightarrow v  = \left( { - 2;\,1;\,1} \right)\), góc giữa hai vectơ đã cho bằng \(60^\circ \).

c) Trong không gian với hệ tọa độ \[Oxyz\], cho hình lăng trụ đứng \(ABC.A'B'C'\) có \(A\left( {0;0;0} \right)\), \(B\left( {2;0;0} \right)\), \(C\left( {0;2;0} \right)\) và \(A'\left( {0;0;2} \right)\). Góc giữa \(BC'\) và \(A'C\) là \(90^\circ \).

d) Trong không gian \(Oxyz\), gọi \(\varphi \) là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), với \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \), khi đó \(\cos \varphi \) bằng\(\frac{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}{{\overrightarrow a .\overrightarrow b }}\).

Hình minh họa sơ đồ một ngôi nhà trong không gian Oxyz, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

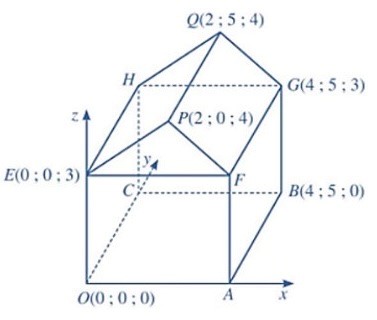
Xét tính đúng sai các mệnh đề sau:

a) Toạ độ điểm \(F(4\,;\,0\,;3)\).

b) Toạ độ vectơ \(\overrightarrow {AH}  = (4\,;\,5\,;\,3)\).

c) \(\overrightarrow {AH} .\overrightarrow {AF}  = 3\).

d) Góc đốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng \[FG\], hai mặt lần lượt là \[\left( {FGQP} \right)\] và \[\left( {FGHE} \right)\] bằng \(26,6^\circ \)(làm tròn kết quả đến hàng phần mười)

Phần III. Câu hỏi trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Cho hai vectơ \(\vec a,\,\vec b\) thỏa mãn: \(\left| {\vec a} \right| = 3,\,\left| {\vec b} \right| = 4,\,\left| {\vec a + \vec b} \right| = 6\). Tính \(\left| {\vec a - \vec b} \right|\). (Làm tròn kết quả đến hàng phần trăm).

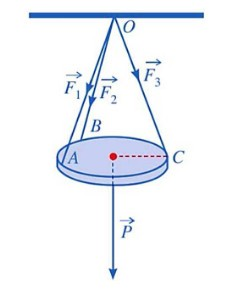
Một chiếc đèn trang trí hình tròn được treo song song với mặt phẳng trần nhà nằm ngang bởi ba sợi dây không giãn \(OA,\,OB,\,OC\) đôi một vuông góc (như hình vẽ dưới đây). Biết lực căng dây tương ứng trên mỗi dây \(OA,\,OB,\,OC\) lần lượt là \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \) thỏa mãn \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 16\](N). Tính trọng lượng (đơn vị: N) của chiếc đèn đó. (Làm tròn kết quả đến hàng phần chục).

Trong không gian tọa độ Oxyz cho 2 điểm \(\,B\left( {2;1;0} \right);\,\,C\left( {1;4;5} \right).\)Điểm \(M(x;y;z)\) thuộc trục hoành sao cho \(MB = MC\). Khi đó giá trị \(2x + y + z\)bằng bao nhiêu?

Trong không gian tọa độ Oxyz cho \(\overrightarrow a \) và \(\overrightarrow b \) tạo với nhau một góc \(120^\circ \). Biết rằng    \(\left| {\overrightarrow a } \right| = 4\,;\,\,\left| {\overrightarrow b } \right| = 3\), tính giá trị của biểu thức \(A = \left| {\overrightarrow a  - \overrightarrow b } \right| + \left| {\overrightarrow a  + \overrightarrow b } \right|\) ( làm tròn kết quả đến hàng phần trăm)

Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao \(30{\rm{\;m}}\) và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.

Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ \(Oxyz\) (đơn vị độ dài trên mỗi trục là \(1{\rm{\;m}})\), các đỉnh của bốn chiếc cột lần lượt là các điểm \(M\left( {90;0;30} \right)\), \(N\left( {90;120;30} \right),P\left( {0;120;30} \right),Q\left( {0;0;30} \right)\).

Giả sử \({K_0}\) là vị trí ban đầu của camera có cao độ bằng 25 và \({K_0}M = {K_0}N = {K_0}P = {K_0}Q\). Để theo dõi quả bóng đến vị trí \(A\), camera được hạ thấp theo phương thẳng đứng xuống điểm \({K_1}\) cao độ bằng 19.

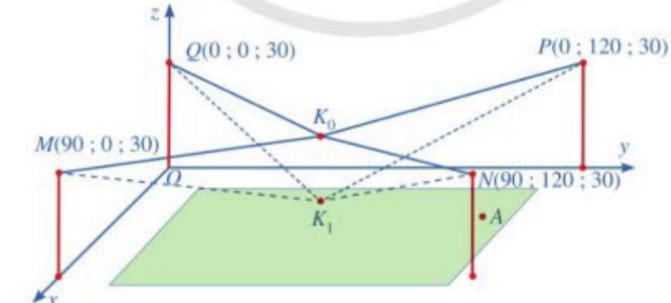
Tọa độ của vectơ \(\overrightarrow {{K_0}{K_1}}  = \left( {a;b;c} \right)\)với \(a,b,c\) là các số thực. Tính \(P = a + b - c\)?

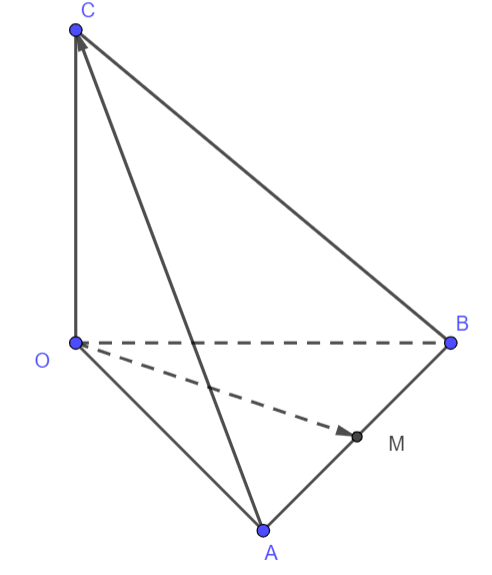
Cho tứ diện OABC có các cạnh OA,OB,OC đôi một vuông góc và OA = OB = OC = 1. Gọi M là trung điểm của cạnh AB. Cô sin góc giữa hai vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {AC} \) bằng \( - \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính \(Q = a.b\)?