Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) - Đề 3
22 câu hỏi
PHẦN 1. TRẮC NGHIỆM 4 PHƯƠNG ÁN (12 CÂU)
Cho hình chóp \[S.ABCD\] có đáy là hình bình hành tâm \[O\]. Đẳng thức nào sau đây là sai?
\(\overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow {BA} + \overrightarrow {DC} \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \).
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {BD} \).
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có cạnh \[a\]. Gọi \[M\] là trung điểm \[AD\]. Giá trị \(\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} \) là:
\({a^2}\).
\[\frac{1}{2}{a^2}\].
\[\frac{3}{2}{a^2}\].
\[\frac{3}{4}{a^2}\].
Trong không gian với hệ tọa độ Oxyz, cho điểm \(A\left( {3; - 1;5} \right)\). Tọa độ của vectơ \(\overrightarrow {OA} \)là
\(\left( {3;1;5} \right)\).
\(\left( {3; - 1;5} \right)\).
\(\left( { - 3; - 1;5} \right)\).
\(\left( { - 3;1; - 5} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(M\left( {\frac{1}{2};1; - 3} \right)\) và \(N\left( {\frac{1}{2}; - 2;4} \right)\). Tọa độ của vectơ \[\overrightarrow {MN} \] là:
\(\left( {1; - 1;1} \right)\).
\(\left( {0; - 3;7} \right)\).
\(\left( {0;3; - 7} \right)\).
\(\left( {\frac{1}{2}; - \frac{1}{2};\frac{1}{2}} \right)\).
Trong không gian Oxyz, cho ba điểm \(A\left( {3;5; - 1} \right),\,\,B\left( {7;x;1} \right)\)và \(C\left( {9;2;y} \right).\) Để \(A,\,\,B,\,\,C\)thẳng hàng thì giá trị \(x + y\) bằng
\(5.\)
\(6.\)
\(4.\)
\(7.\)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm \(A\left( {0; - 1;2} \right)\) và \(B\left( {1; - 2;3} \right)\). Toạ độ của vectơ \(3\overrightarrow {AB} \) là
\(\left( {3;3;3} \right)\).
\(\left( {3; - 3;3} \right)\).
\(\left( { - 3;3;3} \right)\).
\(\left( { - 3; - 3;3} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow u = \left( {3; - 1;1} \right){\rm{ v}}\mu {\rm{ }}\overrightarrow v = \left( {1;2; - 2} \right)\). Độ dài của vectơ \(\overrightarrow u + \overrightarrow v \) là
\(\sqrt {10} \).
\(\sqrt {11} + 3\).
\(3\sqrt 2 \).
\(5\).
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \(A\left( { - 2;\,1;\,0} \right)\), \(B\left( {0;\, - 2;\,5} \right)\), \(C\left( {6; - 2;1} \right)\). Tích vô hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là
\(\sqrt {38} .\sqrt {52} \).
\( - \sqrt {38} .\sqrt {52} \).
\(8\).
\( - 8\).
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm \(A\left( {2;1;1} \right)\) và \(B\left( { - 1;2;1} \right)\). Tìm tọa độ \[A'\] đối xứng với \(A\) qua \(B\).
\(A'\left( {3;4; - 3} \right)\).
\(A'\left( { - 4;3;1} \right)\).
\(A'\left( {4; - 3;3} \right)\).
\(A'\left( {4;33} \right)\).
Cho hai điểm \(M\left( {0\,;\,0\,;\,2} \right)\) và \(N\left( {4\,;\, - 2;\,6} \right)\). Tìm tọa độ điểm \(P\) sao cho \(N\) là trung điểm của MP?
\(P\left( {2\,;\, - 1\,;\,4} \right)\).
\(\left( {4\,;\, - 2\,;\,4} \right)\).
\(\left( {2\,;\, - 1\,;\,2} \right)\).
\(P\left( {8\,;\, - 4\,;\,10} \right)\).
Cho tam giác \(MNP\)có \(M\left( { - 1;3} \right),N\left( {2;2} \right),P\left( { - 1;1} \right).\)Trọng tâm \(G\) của tam giác\(MNP\) có tọa độ là
\(\left( {0;2} \right).\)
\(\left( {0;6} \right).\)
\(\left( {2;0} \right).\)
\(\left( {0; - 2} \right).\)
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm \(M\left( {600;400;20} \right)\)đến điểm \(N\left( {800;500;30} \right)\)trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 15 phút tiếp theo bằng bao nhiêu?
\[\left( {700;500;30} \right)\].
\[\left( {900;650;55} \right)\].
\[\left( {900;550;35} \right)\].
\[\left( {800;540;30} \right)\].
PHẦN 2. CÂU HỎI DẠNG ĐÚNG – SAI (4 CÂU)
Cho hình lăng trụ tam giác đều ABC.A'B'C' có \[AB = a\] và \[AA' = a\sqrt 2 \]. Các mệnh đề dưới đây đúng hay sai?
a) \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \)
b) Gọi \[M\] là trung điểm \(BC\) khi đó \(\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} \).
c) \(\overrightarrow {A'M} .\overrightarrow {AC} = \frac{{{a^2}\sqrt 3 }}{4}\).
d) Góc giữa vectơ \[\overrightarrow {AB'} \] và \(\overrightarrow {BC'} \) bằng \(60^\circ \).
Trong không gian với hệ tọa độ Oxyz cho tam giác \[{\rm{ABC}}\] có các đỉnh \(A\left( {1; - 2;0} \right)\), \(B\left( {2;1; - 2} \right)\), \(C\left( {0;3;4} \right)\).
a) [Mức độ 1] Tọa độ của véc tơ \(\overrightarrow {AB} \) là \(\left( {1;3; - 2} \right)\).
b) [Mức độ 2] Tọa độ trọng tâm của tam giác \(ABC\) là \(G\left( {1;\frac{2}{3};\frac{2}{3}} \right)\).
c) [Mức độ 1] Tọa độ hình chiếu của điểm \(B\) trên mặt phẳng \(Oxy\) là \(H\left( {0;0; - 2} \right)\) .
d) [Mức độ 2] \(\overrightarrow x = 2\overrightarrow {AB} - 3\overrightarrow {BC} \). Tọa độ của véc tơ \(\overrightarrow x = \left( { - 4;12;14} \right)\)
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm \(A\left( {0\,;\, - 1;\,1} \right)\), \(B\left( { - 2\,;\,1;\, - 1} \right)\), \(C\left( { - 1;\,3;\,2} \right)\),\(D\left( { - 1;\,0;\,0} \right)\).
a) Ba điểm \(A,\,B,\,C\) không thẳng hàng.
b) Ba điểm \(A,\,B,\,D\) thẳng hàng.
c) Cosin của góc giữa \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \) bằng \( - \frac{{\sqrt {42} }}{{21}}\).
d) Bốn điểm \(A;\,B;\,C;\,D\) không đồng phẳng.
Cho 3 điểm \(A\left( { - 1\,;\,2;\,1} \right);B\left( {2; - 2;4} \right);C\left( {0; - 4;1} \right)\).
a) Ba điểm \(A,\,B,C\) không thẳng hàng.
b) Điểm \(D\left( {5; - 6;7} \right)\). Khi đó 3 điểm \(A,B,D\) thẳng hàng .
c) \[cos\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \frac{{37}}{{\sqrt {1258} }}\].
d) Cho \(\overrightarrow u \left( {x - 1;2y + 1;3z - 5} \right)\) thoả mãn \(\overrightarrow u \bot \overrightarrow {AB} ;\overrightarrow u \bot \overrightarrow {AC} \). Khi đó \({x^2} + {y^2} + {z^2} = 2024\)
PHẦN 3. CÂU HỎI TRẢ LỜI NGẮN (6 CÂU)
(1,0 điểm) Cho hình lập phương ABCD.A'B'C'D' có cạnh là \(a\). Gọi \(G\) là trọng tâm tam giác \(B'C'D'\), \(I\) là trung điểm của \(AB'\) . Hãy xác định \[cos\left( {\overrightarrow {A'D} \,,\,\overrightarrow {IG} } \right)\]?
Trong không gian với hệ tọa độ Oxyz cho hình hộp ABCD.A'B'C'D'. Biết \[A\left( {2;\,4;\,0} \right)\], \[B\left( {4;\,0;\,0} \right)\], \[C\left( { - 1;\,4;\, - 7} \right)\]và \[D'\left( {6;\,8;\,10} \right)\]. Tìm tọa độ đỉnh \[B'\] của hình hộp ?
Cho 3 điểm . Tìm một vectơ khác \(\overrightarrow 0 \) vuông góc với với cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)?
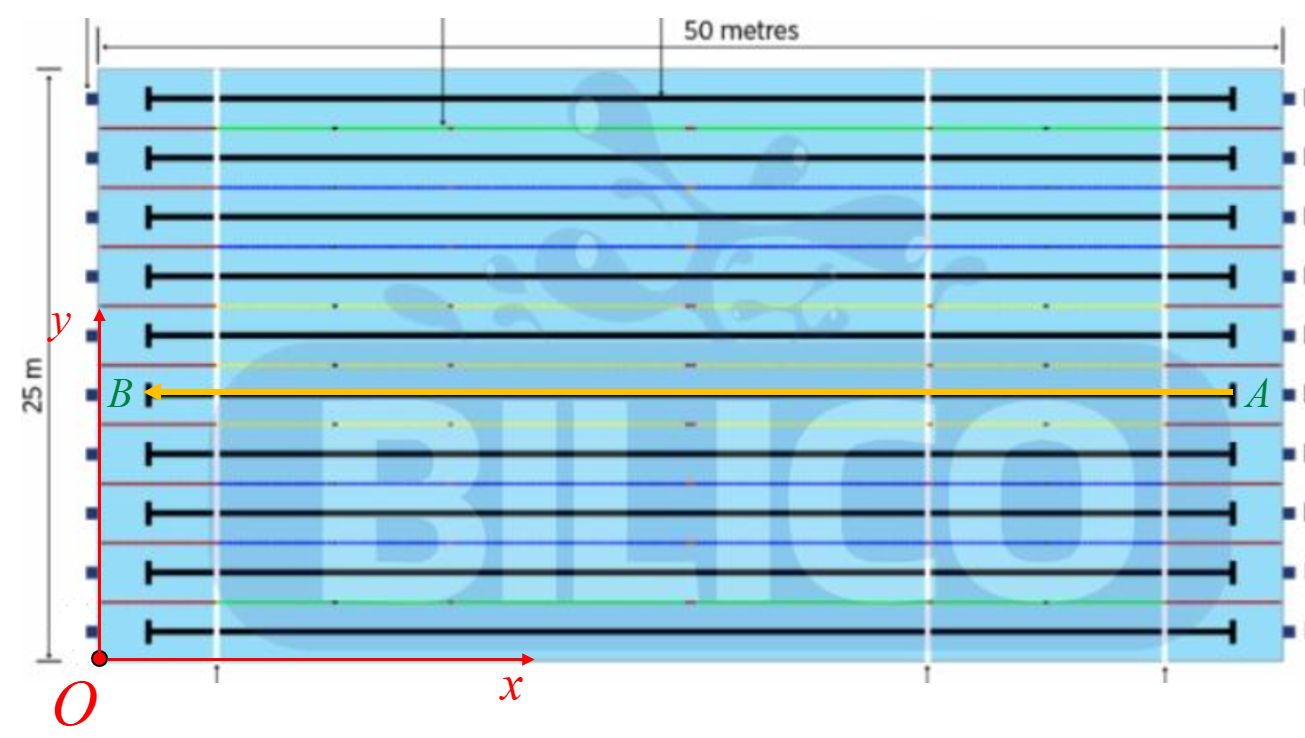
Hình bên dưới mô tả một hồ bơi theo tiêu chuẩn với kích thước như hình vẽ và biết chiều sâu của hồ bơi là 2 m. Biết hồ bơi này có 10 làn bơi với độ rộng như nhau và mỗi làn bơi được ngăn cách bằng phao ngăn phân làn nổi trên mặt nước. Chọn hệ trục \(Oxyz\) như hình bên dưới sao cho gốc tọa độ \(O\) nằm ở dưới đáy của hồ và chiều của vectơ \[\overrightarrow k \] hướng dọc thẳng đứng lên từ đáy bể lên miệng bể. Gọi \(AB\) là là phao ngăn phân làn như hình vẽ và có độ dài là 40 m. Biết hai điểm \(A\) và \(B\) cách đều hai bên thành hồ ứng với chiều rộng của hồ. Hãy xác định tọa độ của vectơ \(\overrightarrow {AB} \).

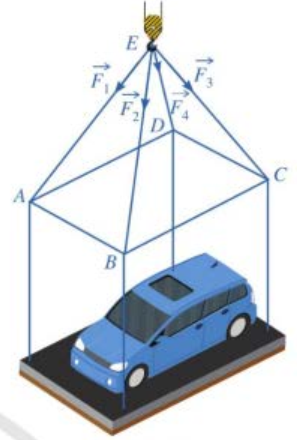
Một chiếc ô tô được đặt trên mặt đáy dưới một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng \(\left( {ABCD} \right)\) song song với mặt mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiến cần cẩu sao cho các đoạn dây cáp \(EA,EB,EC,ED\)có độ dài bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc \({60^0}\) như hình vẽ. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \) đều có cường độ \(5000\left( N \right)\) và trọng lượng khung sắt là \(2000\left( N \right)\). Tính trọng lượng của chiếc xe ô tô (làm tròn đến hàng đơn vị).
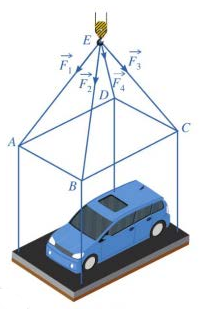
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng \({45^0}\). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết trọng lượng chiếc xe ô tô là \[4000\,N\] và trọng lượng khung sắt là \[2000N\]; cường độ các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} ,\,\overrightarrow {{F_4}} \) là bằng nhau. Tính cường độ lực căng \(\overrightarrow {{F_1}} \)