Đề kiểm tra Khoảng biến thiên và khoảng tứ phân vị (có lời giải) - Đề 5
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:
Thời gian luyện tập (giờ) | \([0;2)\) | \([2;4)\) | \([4;6)\) | \([6;8)\) | \([8;10)\) |
Số vận động viên | 3 | 8 | 12 | 12 | 4 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
3,6875.
5,417.
\(5,3545\).
7,68.
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
Điện lượng (nghìn mAh) | \([0,9;0,95)\) | \([0,95;1,0)\) | \([1,0;1,05)\) | \([1,05;1,1)\) | \([1,1;1,15)\) |
Số viên pin | 10 | 20 | 35 | 15 | 5 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(0.68\).
\(0.068\).
\(0,608\).
\(0,806\).
Đo cân nặng của 1 lớp gồm \(40\) học sinh lớp 12B
![]()
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(15,5\).
\(13,5\).
\(15,3\).
\(13,3\).
Người ta tiến hành phỏng vấn 40 người về một mẫu áo khoác. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là \(100.\) Kết quả được trình bày trong bảng ghép nhóm sau:
Nhóm | \(\left[ {50;60} \right)\) | \(\left[ {60;70} \right)\) | \(\left[ {70;80} \right)\) | \(\left[ {80;90} \right)\) | \(\left[ {90;100} \right)\) |
|
Tần số | \(4\) | \(5\) | \(23\) | \(6\) | \(2\) | \(N = 40\) |
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(11\).
\(9\).
\(15\).
\(10\).
Bạn Trang thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau.
Chiều cao (cm) Lớp 12C 2 7 12 3 0 1 12D 5 9 8 2 1 0
Chiều cao (cm) | [155; 160) | [160; 165) | [165; 170) | [170; 175) | [175; 180) | [180; 185) |
Lớp 12C | 2 | 7 | 12 | 3 | 0 | 1 |
Lớp 12D | 5 | 9 | 8 | 2 | 1 | 0 |
Nếu so sánh theo khoảng biến thiên thì chiều cao của học sinh lớp nào có độ phân tán lớn hơn?
\(12C\).
\(12D\).
\(12C,12D\).
Không kết luận được.
Tổng hợp tiền lương tháng của một số nhân viên văn phòng được ghi lại như sau (đơn vị: triệu đồng):
Lương tháng (triệu đồng) | \([6;8)\) | \([8;10)\) | \([10;12)\) | \([12;14)\) |
Số nhân viên | 3 | 6 | 8 | 7 |
Giá trị nào sau đây là giá trị ngoại lệ của mẫu số liệu trên
\(3\).
\(9\).
\(15\).
\(10\).
Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):
Lương tháng (triệu đồng) | \([6;8)\) | \([8;10)\) | \([10;12)\) | \([12;14)\) |
Số nhân viên | 3 | 6 | 8 | 7 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(1,75\).
\(3,3\).
\(3,25\).
\(2,3\).
Cho bảng tần số ghép nhóm số liệu thống kê cân nặng của 40 học sinh lớp 11 A trong một trường trung học phổ thông (đơn vị: kilôgam).
Nhóm | Tần số |
\([30;40)\) | 2 |
\([40;50)\) | 10 |
\([50;60)\) | 16 |
\([60;70)\) | 8 |
\([70;80)\) | 2 |
\([80;90)\) | 2 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(7\).
\(14,5\).
\(7,5\).
\(13\).
Số lượng huy chương vàng tại Sea Games 31 được thống kê
Số huy chương | \(\left[ {0;10} \right)\) | \(\left[ {10;50} \right)\) | \(\left[ {50;100} \right)\) | \(\left[ {100;210} \right)\) |
Quốc gia | \(5\) | \(2\) | \(3\) | \(1\) |
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(63,5\).
\(65,3\).
\(60\).
\(67,3\).
Điểm thi của 32 học sinh trong kì thi Tiếng Anh ( thang 100 điểm) được phân bố như sau
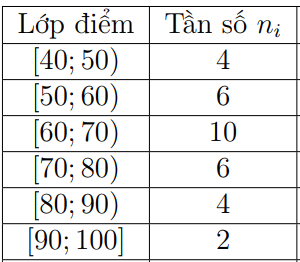
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(25\).
\(20\).
\(15\).
\(10\).
Ta có bảng sau về thời gian tập thể dục buổi sáng của bác Bình và bác An:
Thời gian (phút) | [15; 20) | [20; 25) | [25; 30) | [30; 35) | [35; 40) |
Bác Bình | 5 | 12 | 8 | 3 | 2 |
Bác An | 0 | 25 | 5 | 0 | 0 |
Hỏi hiệu khoảng biến thiên của mẫu số liệu của bác An và bác Bình là bao nhiêu?
\(11\).
\(9\).
\(15\).
\(10\).
Số lượng học sinh trên lớp đăng ký tham gia hoạt động Hoa phượng đỏ ở một trường THPT trên địa bàn TP.HCM được cho ở bảng sau:
Điểm số | \([6;10)\) | \([11;15)\) | \([16;20)\) | \([21;25)\) |
Số học sinh | 4 | 8 | 2 | 6 |
Giá trị nào sau đây là giá trị ngoại lệ của mẫu số liệu trên
\(38\).
\(9\).
\(15\).
\(10\).
Người ta đo đường kính của 61 cây gỗ được trồng sau 12 năm (đơn vị: centimét), họ thu được bảng tần số ghép nhóm sau:\([30;35)\)
Đường kính | \([20;25)\) | \([25;30)\) |
| \([35;40)\) | \([40;45)\) |
Số cây | 4 | 12 | 26 | 13 | 6 |
a) Số cây có đường kính từ 20 cm đến dưới 30 cm là 16 cây.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 25 cm.
c) Để chọn ra 50% các cây gỗ có đường kính lớn nhất thì ta nên chọn các cây gỗ có đường kính (làm tròn đến hàng phần trăm) từ \(32,79\;{\rm{cm}}\)trở lên.
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là 6,75 cm.
Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở bảng đây (đơn vị: kg)
Cân nặng \(\left( {kg} \right)\) | \([1,0;1,1)\) | \([1,1;1,2)\) | \([1,2;1,3)\) | \([1,3;1,4)\) |
Số con giống A | 8 | 28 | 32 | 17 |
Số con giống B | 13 | 14 | 24 | 14 |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với giống B là \[1\;{\rm{kg}}{\rm{.}}\]
b) Cân nặng trung bình của giống \({\rm{B}}\) là: \(1,21\;{\rm{kg}}{\rm{.}}\)
c) Cân nặng trung bình của giống A lớn hơn cân nặng trung bình của giống
d) Nếu so sánh theo khoảng tứ phân vị thì giống A có cân nặng đồng đều hơn giống
Kết quả điều tra về số giờ làm thêm trong 1 tuần của một nhóm sinh viên được cho ở bảng sau
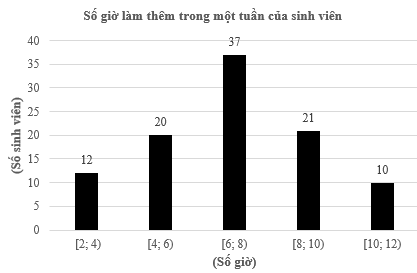
a) Có 32 học sinh làm thêm từ 2 giờ đến dưới 4 giờ trong một tuần.
b) Thời gian làm việc trung bình của nhóm sinh viên trong một tuần là \(6,94\) giờ.
c) Số sinh viên làm thêm trong một tuần (làm tròn đến hàng phần trăm) xấp xỉ \(7,03\) giờ là nhiều nhất.
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên (làm tròn đến hàng phần trăm) là \[3,21.\]
Giả sử kết quả khảo sát hai khu vực A và B về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:
Tuổi kết hôn | \[\left[ {19;22} \right)\] | \[\left[ {22;25} \right)\] | \[\left[ {25;28} \right)\] | \[\left[ {28;31} \right)\] | \[\left[ {31;34} \right)\] |
Số phụ nữ khu vực A | 10 | 27 | 31 | 25 | 7 |
Số phụ nữ khu vực B | 47 | 40 | 11 | 2 | 0 |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là 15.
b) Có 27 phụ nữ ở cả hai khu vực A và B kết hôn trong độ tuổi từ 28 đến dưới 31.
c) Nếu so sánh theo khoảng biến thiên thì phụ nữ ở khu vực A có độ tuổi kết hôn đồng đều hơn.
d) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn.
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Tìm hiệu của khoảng biến thiên và khoảng tứ phân vị trong mẫu số liệu trên ( làm tròn đến hàng phần trăm)?
Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
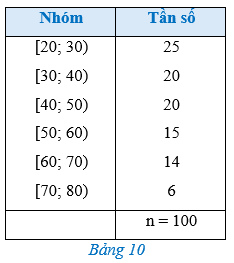
Tìm hiệu giữa khoảng biến thiên và trung vị của mẫu số liệu trên ?
Bảng dưới thống kê điểm trung bình cuối năm của các học sinh lớp \(11{\rm{\;A}}\) và 11B ở bảng sau:
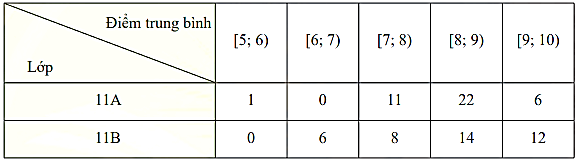
Gọi \[A,B\]lần lượt là khoảng biến thiên của lớp 11A và lớp 11B. Tính \({A^2} - {B^2}\).
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng sau.
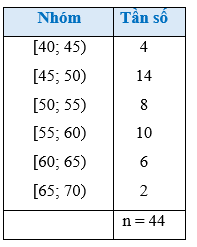
Tìm hiệu giữa khoảng biến thiên và khoảng tứ phân vị của bảng số liệu trên ?
Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu \(A\) và \(B\) trong 50 ngày giao dịch liên tiếp.

Tính hiệu giữa hai khoảng tứ phân vị của cổ phiếu A và cổ phiếu B (làm tròn đến hàng phần chục)?
Kết quả 40 lần nhảy xa của một vận động viên được thống kê trong bảng sau
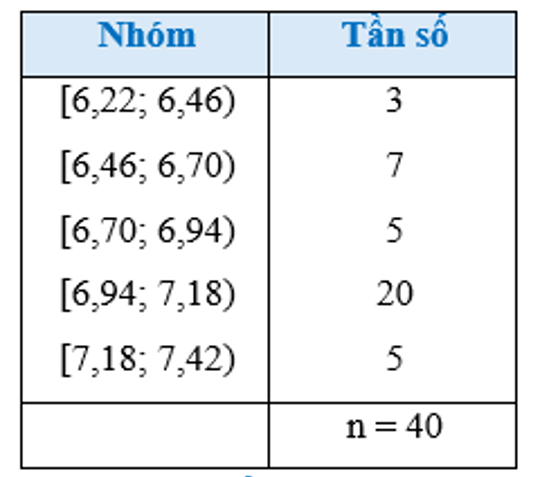
Tìm hiệu giữa khoảng tứ phân vị và trung vị của mẫu số liệu trên (làm tròn đến hàng phần chục) ?