Đề kiểm tra Khoảng biến thiên và khoảng tứ phân vị (có lời giải) - Đề 4
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau.
Tuổi thọ | \([2;3,5)\) | \([3,5;5)\) | \([5;6,5)\) | \([6,5;8)\) |
Số bóng đèn | 8 | 22 | 35 | 15 |
Khoảng biến thiên của mẫu số liệu trên là
\(3\).
\(6\)
\(5,5\).
\(4,5\).
Kết quả khảo sát cân nặng của 25 quả cam ở lô hàng A được cho ở bảng sau:
Cân nặng (g) | \([150;155)\) | \([155;160)\) | \([160;165)\) | \([165;170)\) | \([170;175)\) |
Số quả cam ở lô hàng A | 1 | 3 | 7 | 10 | 4 |
Khoảng biến thiên của mẫu số liệu trên là
\(15\).
\(25\)
\(20\).
\(16\).
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | \([0;20)\) | \([20;40)\) | \([40;60)\) | \([60;80)\) | \([80;100)\) |
Số học sinh | 5 | 9 | 12 | 10 | 6 |
Khoảng biến thiên của mẫu số liệu trên là
\(80\).
\(60\)
\(100\).
\(7\).
Khảo sát cân nặng của 30 bạn học sinh (đơn vị: kilogam), ta có bảng tần số ghép nhóm:
Cân nặng(m) | [15;20) | [20;25) | [25;30) | [30;35) | [35;40) | [40;45) | [45;50) | [50;55) |
Số học sinh | 1 | 0 | 0 | 1 | 10 | 17 | 0 | 1 |
Khoảng biến thiên của mẫu số liệu trên là
\(45\).
\(16\)
\(40\).
\(35\).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu | \([5;7)\) | \([7;9)\) | \([9;11)\) | \([11;13)\) | \([13;15)\) |
Số ngày | 2 | 7 | 7 | 3 | 1 |
Khoảng biến thiên của mẫu số liệu trên là
\(8\).
\(6\)
\(10\).
\(9\).
Một cuộc khảo sát đã tiến hành xác định tuổi (theo năm) của 120 chiếc ô tô. Kết quả điểu tra được cho trong bảng sau.
Số tuổi ( theo năm) | [0;4) | [4;8) | [8;12) | [12;16) | [20;24) |
Số ô tô | 23 | 25 | 37 | 26 | 19 |
Khoảng biến thiên của mẫu số liệu trên là
\(16\).
\(20\)
\(24\).
\(4\).
Anh Ba ghi nhận lại kết quả ném lao của mình ở cự li 30 lần, và có bảng sau:
Cự li (m) | [69,2;70) | [70;70,8) | [70,8;71,6) | [71,6;72,4) | [72,4;73,2) |
Số lần | 4 | 2 | 9 | 10 | 5 |
Khoảng biến thiên của mẫu số liệu trên là
\(5\).
\(6\)
\(4\).
\(9\).
Số khách hàng nam mua bảo hiểm ở từng độ tuổi được thống kê như sau:
Độ tuối | \([20;30)\) | \([30;40)\) | \([40;50)\) | \([50;60)\) | \([60;70)\) |
Số khách hàng nam | 4 | 6 | 10 | 7 | 3 |
Khoảng biến thiên của mẫu số liệu trên là
\(40\).
\(30\)
\(50\).
\(10\).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu | \([5;7)\) | \([7;9)\) | \([9;11)\) | \([11;13)\) | \([13;15)\) |
Số ngày | 2 | 7 | 7 | 3 | 1 |
Khoảng tứ phân vị của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
\(11\).
\(8\).
\(3\).
\(2\).
Câu 1: Bảng sau thống kê cân nặng của 30 học sinh lớp 12A1
Cân nặng (Kg) | \(\left[ {45;50} \right)\) | \(\left[ {50;55} \right)\) | \(\left[ {55;60} \right)\) | \(\left[ {60;65} \right)\) | \(\left[ {65;70} \right)\) |
Số học sinh | 5 | 10 | 5 | 8 | 2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
\(25\).
\(5\).
\(45\).
\(70\).
Công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm là
\({\Delta _Q} = {Q_3} - {Q_1}\).
\({\Delta _Q} = {Q_1} - {Q_3}\).
\({\Delta _Q} = {Q_3}.{Q_1}\).
\({\Delta _Q} = {Q_3} + {Q_1}\).
Bảng sau thống kê cân nặng của 30 quả đu đủ được lựa chọn ngẫu nhiên sau khi thu hoạch ở vườn nhà Lan
Cân nặng (g) | \(\left[ {750;800} \right)\) | \(\left[ {800;850} \right)\) | \(\left[ {850;900} \right)\) | \(\left[ {900;950} \right)\) | \(\left[ {950;1000} \right)\) |
Số quả bưởi | 5 | 10 | 5 | 8 | 2 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
\(103,125\).
\(1728,125\).
\(250\).
\(750\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Dựa vào bảng tần số mẫu số liệu ghép nhóm sau, hãy xét tính đúng sai của các mệnh đề bên dưới:
Nhóm | \([30;40)\) | \([40;50)\) | \([50;60)\) | \([60;70)\) | \([70;80)\) | \([80;90)\) |
Tần số | 2 | 10 | 16 | 8 | 2 | 2 |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \[50.\]
b) Nhóm chứa mốt là nhóm \([50;60).\)
c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là: \({Q_1} = 48.\)
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[14,5.\]
Khảo sát thời gian (tính bằng giây) chạy cự ly 100 m của 39 học sinh nam, giáo viên thu được mẫu số liệu ghép nhóm sau
Thời gian (giây) | \[\left[ {15;17} \right)\] | \[\left[ {17;19} \right)\] | \[\left[ {19;21} \right)\] | \[\left[ {21;23} \right)\] | \[\left[ {23;25} \right)\] |
Số học sinh | 2 | 5 | 10 | 7 | 15 |
a) Thành tích từ 23 giây đến dưới 25 giây có 15 học sinh.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 13.
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \[4,15.\]
d) Số học sinh đạt thành tích chạy (làm tròn đến hàng phần trăm) xấp xỉ 23,7 giây là nhiêu nhất
Khảo sát điểm trung bình môn Toán của một số học sinh lớp 12 được cho ở bảng sau:
Khoảng điểm | \([6,5;7)\) | \([7;7,5)\) | \([7,5;8)\) | \([8;8,5)\) | \([8,5;9)\) | \([9;9,5)\) | \([9,5;10)\) |
Số học sinh | 8 | 10 | 16 | 24 | 13 | 7 | 4 |
a) Có 80 học sinh tham gia khảo sát.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 4.
c) Có nhiều hơn 50% số học sinh đạt ít nhất 8 điểm.
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là 1,04.
Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau:
Lượng nước tiêu thu \(\left( {{m^3}} \right)\) | \[\left[ {3;\;6} \right)\] | \[\left[ {6;\;9} \right)\] | \[\left[ {9;\;12} \right)\] | \[\left[ {12;\;15} \right)\] | \[\left[ {15;\;18} \right)\] |
Số hộ gia đình | 24 | 57 | 42 | 29 | 8 |
a) Có 42 hộ gia đình tiêu thụ lượng nước từ \[9\;{{\rm{m}}^3}\] đến dưới \[12\;{{\rm{m}}^3}.\]
b) Mốt của mẫu số liệu ghép nhóm trên là \(8,0625.\)
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên xấp xĩ \[5,68.\]
d) Công ty muốn gửi một thông báo khuyến nghị tiết kiệm nước đến 25% các hộ gia đình có lượng nước tiêu thụ cao nhất thì công ty nên gửi thông báo tiết kiệm nước đến các hộ gia đình có lượng nước tiêu thụ từ \(8,95\;{{\rm{m}}^3}\) nước trở lên.
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

Tìm khoảng biến thiên của mẫu số liệu trên ?
Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:
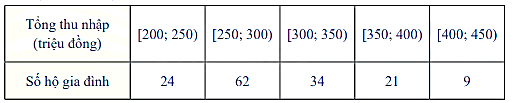
Tìm khoảng tứ phân vị của mẫu số liệu trên (kết quả làm tròn đến hàng phần mười) ?
Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình của nam giới và nữ giới ở 50 quốc gia.
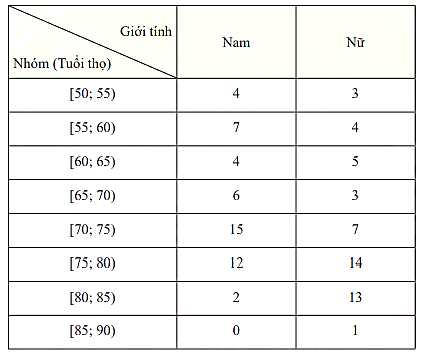
Gọi \(A,B\)lần lượt là khoảng tứ phân vị của nhóm tuổi thọ trung bình của nam và nữ. Tính \(A - B\)( làm tròn đến hàng phần mười).
Cho mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng).
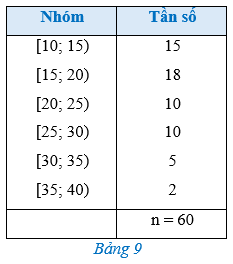
Tìm hiệu giữa khoảng biến thiên và trung vị của mẫu số liệu trên(làm tròn đến hàng phần chục)?
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Tìm hiệu của khoảng biến thiên và khoảng tứ phân vị trong mẫu số liệu trên ( làm tròn đến hàng phần trăm)?
Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
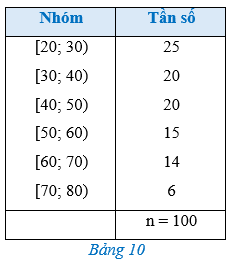
Tìm hiệu giữa khoảng biến thiên và trung vị của mẫu số liệu trên ?