Đề kiểm tra Khoảng biến thiên và khoảng tứ phân vị (có lời giải) - Đề 3
22 câu hỏi
Khảo sát thời g
Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
![]()
Khoảng biến thiên \(R\) của mẫu số liệu ghép nhóm trên là
\(R = 20\).
\(R = 100\).
\(R = 50\).
\(R = 60\).
Biết \({Q_1},\,{Q_2},\,{Q_3}\) là tứ phân vị thứ nhất, tứ phân vị thứ hai và tứ phân vị thứ ba của một mẫu số liệu ghép nhóm. Khi đó khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu đó là
\({\Delta _Q} = {Q_3} - {Q_1}\).
\({\Delta _Q} = {Q_1} - {Q_3}\).
\({\Delta _Q} = {Q_2} - {Q_1}\).
\({\Delta _Q} = {Q_3} - {Q_2}\).
Thống kê thời gian sử dụng mạng xã hội trong ngày của các bạn học sinh tổ 1 và tổ 2 lớp 12A thu được bảng sau:

Tìm khoảng biến thiên \({R_1},\,{R_2}\)cho thời gian sử dụng mạng xã hội của tổ 1 và tổ 2.
\({R_1} = 60;\,\,{R_2} = 90\).
\({R_1} = 90;\,\,{R_2} = 60\).
\({R_1} = 30;\,\,{R_2} = 30\).
\({R_1} = 10;\,\,{R_2} = 30\).
Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết quả sau:

Tìm khoảng biến thiên cho mẫu số liệu ghép nhóm trên
\(20\).
\(15\).
\(16\).
\(4\).
Tìm hiểu thời gian chạy cự li \(1000m\) ( đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Nhóm \(\left[ {131;133} \right)\) có tần số là
\(3\).
\(15\).
\(10\).
\(7\).
Cho mẫu số liệu ghép nhóm về khối lượng (đơn vị: gram) của \(30\) củ khoai tây như sau:

Giá trị đại diện của nhóm \(\left[ {90;100} \right)\)
\(85\).
\(95\).
\(90\).
\(100\).
Cho mẫu số liệu ghép nhóm về độ tuổi của dân cư của khu phố \(A\) như sau

Khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là (làm tròn đến hàng phần trăm).
\(30,38\).
\(63,33\).
\(32,95\).
\(32,94\).
Ta có bảng sau về thời gian tập thể dục buổi sáng của bác Bình và bác An:
Thời gian (phút) | [15; 20) | [20; 25) | [25; 30) | [30; 35) | [35; 40) |
Bác Bình | 5 | 12 | 8 | 3 | 2 |
Bác An | 0 | 25 | 5 | 0 | 0 |
Hỏi hiệu khoảng biến thiên của mẫu số liệu của bác Bình và bác An là bao nhiêu?
\(11\).
\(9\).
\(15\).
\(10\).
Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):
Lương tháng (triệu đồng) | \([6;8)\) | \([8;10)\) | \([10;12)\) | \([12;14)\) |
Số nhân viên | 3 | 6 | 8 | 7 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
\(1,75\).
\(3,3\).
\(3,25\).
\(2,3\).
Số lượng học sinh trên lớp đăng ký tham gia hoạt động Hoa phượng đỏ ở một trường THPT trên địa bàn TP.HCM được cho ở bảng sau:
Điểm số | \([6;10)\) | \([11;15)\) | \([16;20)\) | \([21;25)\) |
Số học sinh | 4 | 8 | 2 | 6 |
Giá trị nào sau đây là giá trị ngoại lệ của mẫu số liệu trên
\(38\).
\(9\).
\(15\).
\(10\).
Các bạn học sinh lớp 12A5 trả lời 40 câu hỏi trong một bải kiểm tra. Kết quả số câu trả lời đúng được thống kê ở bảng sau.
Số câu trả lời đúng | \(\left[ {16;21} \right)\) | \(\left[ {21;26} \right)\) | \(\left[ {26;31} \right)\) | \(\left[ {31;36} \right)\) | \(\left[ {36;41} \right)\) |
Số học sinh | 4 | 8 | 8 | 16 | 4 |
Khoảng tứ phân vị của mẫu số liệu là
\[9,375\].
\[8,625\].
\[10,15\]
\[7,5\].
Cho mẫu số liệu ghép nhóm về chiều cao của \(25\) cây cam giống như sau:

Từ một mẫu số liệu về chiều cao của cây xoài giống người ta tính được khoảng tứ phân vị bằng \(13,94\). Đối với các cây cam giống và xoài giống được khảo sát ở trên, khẳng định nào sau đây đúng
Chiều cao của các cây xoài giống phân tán hơn.
Chiều cao của các cây cam giống phân tán hơn.
Các cây cam và xoài giống có chiều cao phân tán như nhau.
Không so sánh được độ phân tán của các cây cam giống và xoài giống được khảo sát.
Cỡ mẫu: \(n = 4 + 6 + 7 + 5 + 3 = 25\).
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_6} + {x_7}}}{2}\). Do \({x_6},\,\,{x_7}\) đều thuộc nhóm \(\left[ {10;20} \right)\) nên nhóm này chứa \({Q_1}\).
Do đó: \(p = 2\), \({a_2} = 10\), \({m_2} = 6\), \({m_1} = 4\), \({a_3} - {a_2} = 10\). Ta có:
\({Q_1} = 10 + \frac{{\frac{{25}}{4} - 4}}{6}.10 = 13,75\).
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{19}} + {x_{20}}}}{2}\). Do \({x_{19}};\,{x_{20}}\) đều thuộc nhóm \(\left[ {30;\,40} \right)\) nên nhóm này chứa \({Q_3}\).
Cho bảng mẫu số liệu ghép nhóm về mức lương của hai công ty \(A\) và \(B\) (đơn vị : triệu đồng) như sau: 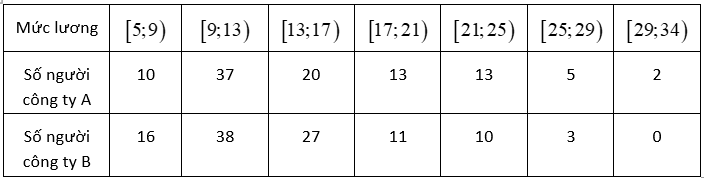
Trong các khẳng định sau , khẳng định nào đúng, khẳng định nào sai?
a) Khoảng biến thiên cho mức lương của hai công ty là \(29\).
b) Khoảng biến thiên cho mức lương của công ty \(B\) là \(24\).
c) Mức lương của công ty \(A\) biến động nhiều hơn mức lương của công ty \(B\).
d) Nhóm chứa tứ phân vị thứ ba của công ty \(A\) là nhóm \(\left[ {17;21} \right)\).
Cho bảng mẫu số liệu ghép nhóm về điểm môn Toán của hai lớp \(12A\) và \(12B\) được cho như sau:
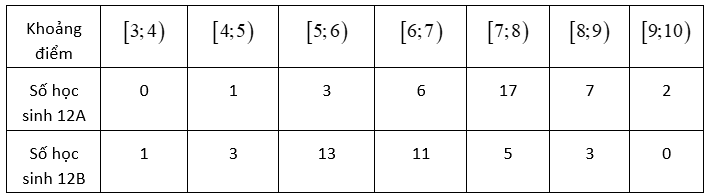
Trong các khẳng định sau , khẳng định nào đúng, khẳng định nào sai?
a) Khoảng biến thiên cho điểm môn Toán của lớp \(12A\) là \(7\).
b) Khoảng biến thiên cho điểm môn Toán của lớp \(12B\) là \(6\).
c) Nhóm chứa tứ phân vị thứ nhất của lớp \(12A\) là nhóm \(\left[ {6;7} \right)\).
d) Nhóm chứa tứ phân vị thứ ba của lớp \(12B\) là nhóm \(\left[ {7;8} \right)\).
Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho ở bảng sau
Thời gian(phút) | \[\left[ {9,5;12,5} \right)\] | \[\left[ {12,5;15,5} \right)\] | \[\left[ {15,5;18,5} \right)\] | \[\left[ {18,5;21,5} \right)\] | \[\left[ {21,5;24,5} \right)\] |
Số học sinh | \[4\] | \[12\] | \[14\] | \[23\] | \[3\] |
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a/ Khoảng biến thiên của mẫu số liệu là \[15\] .
b/ Nhóm chứa tứ phân vị thứ ba là \[\left[ {15,5;18,5} \right)\] .
c/ Tứ phân vị thứ nhất là \[{Q_1} = 15\] .
d/ Khoảng tứ phân vị của mẫu số liệu ghép nhóm bé hơn \[6\] .
Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.
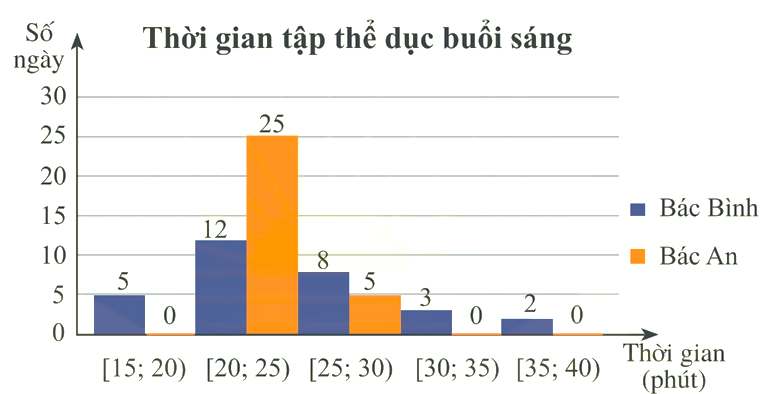
Các mệnh đề sau đúng hay sai?
a) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là \(25\) (phút).
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An là: \({\Delta _Q} = 2\)
c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là: \({Q_3}^\prime = \frac{{455}}{{16}}\)
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An lớn hơn bác Bình
Cho bảng số liệu ghép nhóm về chiều cao ( đơn vị centimét) của 36 học sinh trong lớp 12A1 như sau:

Xác định khoảng biến thiên của mẫu số liệu ghép nhóm?
Cho bảng số liệu ghép nhóm về chiều cao ( đơn vị centimét) của 36 học sinh trong lớp 12A1 như sau:

Nhóm chứa tứ phân vị thứ nhất có tần số bằng bao nhiêu?
Khoảng biến thiên của mẫu số liệu ghép nhóm được cho ở bảng sau là bao nhiêu?
Nhóm | \[\left[ {15;22} \right)\] | \[\left[ {22;29} \right)\] | \[\left[ {29;36} \right)\] | \[\left[ {36;43} \right)\] | \[\left[ {43;50} \right)\] |
Tần số | \[1\] | \[6\] | \[21\] | \[21\] | \[11\] |
Trả lời:………………
Khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho ở bảng sau là bao nhiêu?(làm tròn kết quả đến hai chữ số thập phân).
Nhóm | \[\left[ {25;30} \right)\] | \[\left[ {30;35} \right)\] | \[\left[ {35;40} \right)\] | \[\left[ {40;45} \right)\] |
Tần số | \[2\] | \[17\] | \[10\] | \[25\] |
Trả lời:………………
Số tiền (đơn vị nghìn đồng) mà 60 khách hàng mua sách ở hai cửa hàng \(A,B\) trong một ngày được cho trong 2 bảng sau:
Số tiền (nghìn đồng) | \(\left[ {40;50} \right)\) | \(\left[ {50;60} \right)\) | \(\left[ {60;70} \right)\) | \(\left[ {70;80} \right)\) | \(\left[ {80;90} \right)\) |
Số khách hàng cửa hàng \(A\) | 3 | 6 | 19 | 23 | 9 |
Số tiền (nghìn đồng) | \(\left[ {40;50} \right)\) | \(\left[ {50;60} \right)\) | \(\left[ {60;70} \right)\) | \(\left[ {70;80} \right)\) | \(\left[ {80;90} \right)\) |
Số khách hàng cửa hàng \(B\) | 5 | 9 | 15 | 20 | 11 |
Phương sai của mẫu số liệu ghép nhóm của cửa hàng \(A\) là \(s_A^2\), cửa hàng \(B\) là \(s_B^2\). Khi đó \(s_A^2\)\( - s_B^2\) là: (kết quả làm tròn đến hàng phần chục
Kết quả 40 lần nhảy xa của hai vận động viên Dũng và Huy được lần lượt thống kê trong Bảng 1 và Bảng 2 (đơn vị: mét):
Bảng 1
Nhóm | [6,22; 6,46) | [6,46; 6,70) | [6,70; 6,94) | [6,94; 7,18) | [7,18; 7,42) |
|
Tần số | 3 | 7 | 5 | 20 | 5 | n = 40 |
Bảng 2
Nhóm | [6,22; 6,46) | [6,46; 6,70) | [6,70; 6,94) | [6,94; 7,18) | [7,18; 7,42) |
|
Tần số | 2 | 5 | 8 | 19 | 6 | n = 40 |
Gọi \(a,b\)lần lượt là phương sai của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Dũng và Huy. Khi đó, hiệu số của \(a - b\) bằng bao nhiêu (giả sử các kết quả được lấy hai chữ số thập phân sau dấu phẩy)