Đề kiểm tra Khoảng biến thiên và khoảng tứ phân vị (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
[Mức độ 1] Xét mẫu số liệu ghép nhóm cho bởi bảng sau.
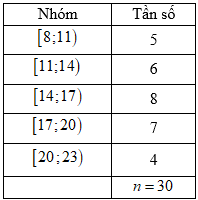
Khoảng biến thiên của mẫu số liệu ghép nhóm bằng
\(3\).
\(8\).
\(31\).
\(15\).
Biểu diễn mẫu số liệu ghép nhóm về cân nặng (đơn vị: kilogam) của 40 học sinh một lớp 12 ở
một trường trung học phổ thông được cho dưới bảng sau.
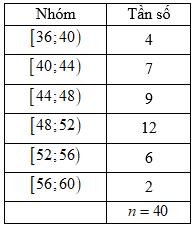
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là
\(24\).
\(4\).
\(12\).
\(6\).
Biểu diễn mẫu số liệu ghép nhóm về tiền điện (đơn vị: nghìn đồng) của 58 hộ gia đình ở một
tổ dân phố được cho dưới bảng sau.
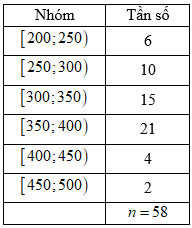
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là
\(21\).
\(50\).
\(300\).
\(299\).
Biểu diễn mẫu số liệu ghép nhóm về thời gian hoàn thành một bài tập (đơn vị: phút) của một
số học sinh được cho dưới bảng sau.
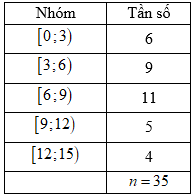
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là
\(11\).
\(15\).
\(3\).
\(12\).
Kết quả điều tra tổng thu nhập trong năm \[2024\] của một số hộ gia đình ở thành phố Nha
Trang được ghi lại ở bảng sau:

Tứ phân vị \({Q_1}\) bằng
\[\frac{{675}}{{62}}\].
\[\frac{{9775}}{{31}}\].
\[\frac{{16715}}{{62}}\].
\[\frac{{16175}}{{62}}\].
Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày
trong quý III năm 2024 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; …
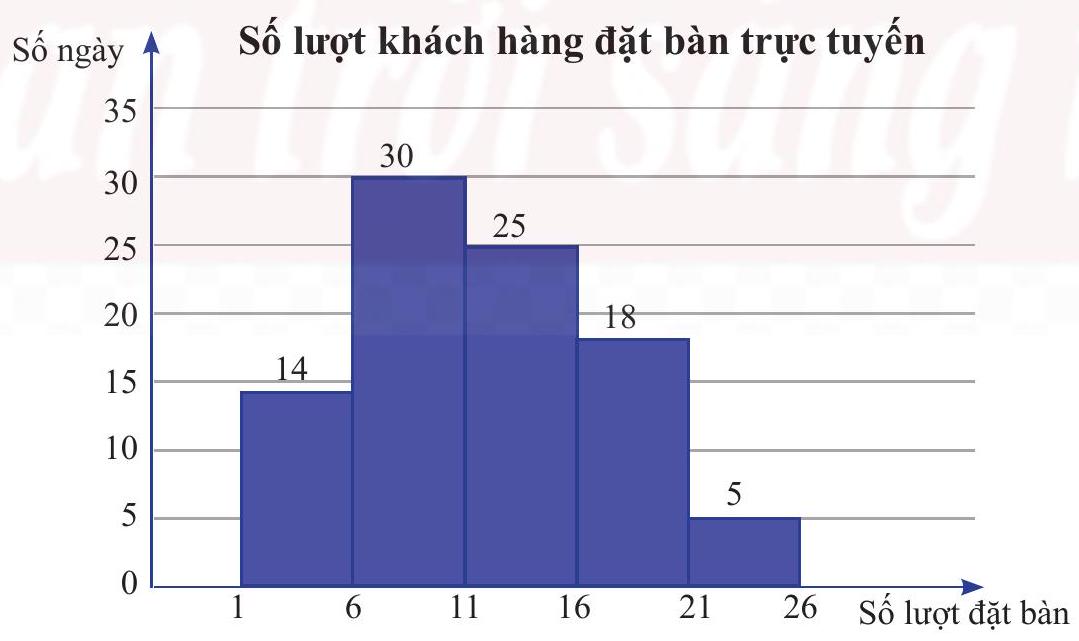
Tứ phân vị \({Q_1}\) bằng
\[13\].
\[15\].
\[18,5\].
\[16\].
Kết quả đo chiều cao của \[100\] cây keo ba năm tuổi tại một nông trường được cho ở bảng sau
![]()
Khoảng tứ phân vị của mẫu số liệu ghép nhóm bằng
\[0,886\].
\[0,115\].
\[0,826\].
\[0,286\].
Bảng số liệu ghép nhóm tổng lượng mưa (đơn vị: mm) đo được vào tháng \[7\] từ năm \[2005\]
đến \[2024\] tại một trạm quan trắc đặt ở Cà Mau
![]()
Khoảng tứ phân vị của mẫu số liệu ghép nhóm bằng
\(375\).
\(175\).
\(225\).
\(200\).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở
bảng sau (đơn vị: triệu đồng).
Doanh thu | \(\left[ {5;7} \right)\) | \(\left[ {7;9} \right)\) | \(\left[ {9;11} \right)\) | \(\left[ {11;13} \right)\) | \(\left[ {13;15} \right)\) |
Số ngày | \(2\) | \(7\) | \(7\) | \(3\) | \(1\) |
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
\(\left[ {7;9} \right)\)
\(\left[ {9;11} \right)\).
\(\left[ {11;13} \right)\).
\(\left[ {13;15} \right)\).
Khảo sát cân nặng của 30 bạn học sinh (đơn vị: kilogam), ta có bảng tần số ghép nhóm:
Cân nặng (kg) | [15;20) | [20;25) | [25;30) | [30;35) | [35;40) | [40;45) | [45;50) | [50;55) |
Số học sinh | 1 | 0 | 0 | 1 | 10 | 17 | 0 | 1 |
Số trung bình cộng của mẫu số liệu ghép nhóm trên bằng
\(20\).
\(32\).
\(37\).
\(40\).
Tìm hiểu thời gian chạy cự li \(1000\,{\rm{m}}\) ( đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Thời gian chạy trung bình cự li \(1000\,{\rm{m}}\) (giây) của các bạn học sinh là
\(130,35\).
\(131,03\).
\(130,4\).
\(132,5\).
Một công ty bảo hiểm thống kê lại độ tuổi các khách hàng mua bảo hiểm xe ô tô ở bảng sau:
![]()
Số trung bình của mẫu số liệu ghép nhóm trên thuộc khoảng nào sau đây?
\(\left[ {25;35} \right)\).
\(\left[ {35;40} \right)\).
\(\left[ {40;45} \right)\).
\(\left[ {45;55} \right)\).
Bảng dưới đây cho ta bảng tần số ghép nhóm số liệu thống kê cân nặng của \(40\)học sinh lớp \(11A\) trong
một trường trung học phổ thông (đơn vị: kilôgam).
Nhóm | Tần số | Tần số tích lũy |
\(\left[ {30;40} \right)\) | 2 | 2 |
\(\left[ {40;50} \right)\) | 10 | 12 |
\(\left[ {50;60} \right)\) | 16 | 28 |
\(\left[ {60;70} \right)\) | 8 | 36 |
\(\left[ {70;80} \right)\) | 2 | 38 |
\(\left[ {80;90} \right)\) | 2 | 40 |
| \(n = 40\) |
|
Xét tính đúng – sai của các mệnh đề sau?
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là \(R = 60\).
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \(\Delta Q = 14,5\).
c) Số trung bình cộng của mẫu số liệu ghép nhóm là \(\bar x = 56\).
d) Phương sai của mẫu số liệu ghép nhóm là \({s^2} = 128\).
sau cho ta bảng tần số ghép nhóm số liệu thống kê chiều cao của 40 học sinh (đơn vị: cm)
Nhóm | Tần số | Tần số tích lũy |
\(\left[ {140;145} \right)\) | 2 | 2 |
\(\left[ {145;150} \right)\) | 3 | 5 |
\(\left[ {150;155} \right)\) | 5 | 10 |
\(\left[ {155;160} \right)\) | 15 | 25 |
\(\left[ {160;165} \right)\) | 10 | 35 |
\(\left[ {165;170} \right)\) | 5 | 40 |
| \(n = 40\) |
|
Xét tính đúng – sai của các mệnh đề sau?
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là \(R = 30\).
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \(\Delta Q = 7\).
c) Số trung bình cộng của mẫu số liệu ghép nhóm là \(\bar x = 159\).
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm là \(s \approx 6,42\).
Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong
một tháng ở bảng sau:
Lượng nước tiêu thụ \(\left( {{m^3}} \right)\) | \([3;6)\) | \([6;9)\) | \([9;12)\) | \([12;15)\) | \([15;18)\) |
Số hộ gia đình | 24 | 57 | 42 | 29 | 8 |
a) Lượng nước tiêu thụ trung bình trong tháng của một hộ gia đình trong khu vực nói trên xấp xỉ bằng \[9,4\,\,\left( {{m^3}} \right).\]
b) Khoảng biến thiên của mẫu số liệu trên là \(R = 15\,\,\left( {{m^3}} \right).\)
c) Công ty muốn gửi một thông báo khuyến nghị tiết kiệm nước đến \(25\% \) các hộ gia đình có lượng nước tiêu thụ cao nhất. Vậy công ty nên gửi thông báo tiết kiệm nước đến các hộ gia đình có lượng nước tiêu thụ từ \(11\,\,\;\left( {{m^3}} \right)\) nước trở lên.
d) Độ lệch chuẩn của mẫu số liệu trên bằng \(3\,\,\left( {{m^3}} \right).\)
Phỏng bạn Hùng và bạn Vương làm thí nghiệm trồng cây. Mỗi bạn trồng 40 cây cần tây trong cốc, phần
gốc của các cây khi bắt đầu trồng đều dài \(4{\rm{\;cm}}\). Bảng 1 và bảng 2 lần lượt biểu diễn mẫu số liệu ghép nhóm về số liệu thống kê chiều cao của các cây (đơn vị: centimét) mà bạn Hùng và bạn Vương trồng sau 5 tuần.
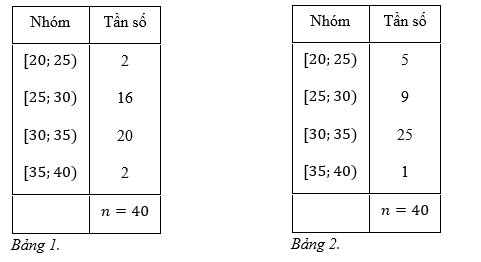
a) Chiều cao trung bình của mỗi cây do hai bạn Hùng và Vương trồng không bằng nhau.
b) Khoảng biến thiên của cả hai mẫu số liệu trên là 20.
c) Khoảng tứ phân vị của mẫu số liệu ở bảng 1 là 5,5.
d) Chiều cao của các cây mà bạn Vương trồng đồng đều hơn các cây mà bạn Hùng trồng.
Khảo sát thời gian (phút) tập thể dục trong ngày của một số học sinh lớp 12 thu được mẫu số liệu ghép nhóm sau:
![]()
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười).
Khảo sát thời gian (phút) tập thể dục trong ngày của một số học sinh lớp 12 thu được mẫu số liệu ghép nhóm sau:
![]()
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười).
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao của 40 học sinh nam lớp 12 ở một trường trung học phổ thông.
Nhóm | Tần số |
\(\begin{array}{l}\left[ {160;163} \right)\\\left[ {163;166} \right)\\\left[ {166;169} \right)\\\left[ {169;172} \right)\\\left[ {172;175} \right)\end{array}\) | 8 10 12 8 2 |
| \(n = 40\) |
Tìm khoảng biến thiên của mẫu số liệu?
Kết quả 40 lần nhảy xa của hai vận động viên Nam được cho như bảng sau
Nhóm | Tần số |
\(\begin{array}{l}\left[ {6,22;6,46} \right)\\\left[ {6,46;6,70} \right)\\\left[ {6,70;6,94} \right)\\\left[ {6,94;7,18} \right)\\\left[ {7,18;7,42} \right)\end{array}\) | 4 6 5 18 7 |
| \(n = 40\) |
Tính phương sai của mẫu số liệu trên (Các kết quả làm tròn đến hàng phần trăm)?
Điểm thi học kì của hai lớp 12A1 và 12A2 cho bởi bảng sau
Điểm thi | \(\left[ {0;2} \right)\) | \(\left[ {2;4} \right)\) | \(\left[ {4;6} \right)\) | \(\left[ {6;8} \right)\) | \(\left[ {8;10} \right]\) |
|
Lớp 12A1 | \(3\) | \(5\) | \(17\) | \(15\) | \(5\) | \(n = 45\) |
Lớp 12A2 | \(2\) | \(8\) | \(15\) | \(14\) | \(6\) | \(n = 45\) |
1) Nhận xét điểm trung bình kiểm tra của cả hai lớp trên( làm tròn kết quả đến hàng phần trăm).
2) Xác định phương sai và độ lệch chuẩn của mẫu số liệu trên về điểm kiểm tra của hai lớp và giải thích số liệu thu được. (Làm tròn kết quả đến hàng phần trăm).
Cho mẫu thống kê trả lương của hai công ty A và B (đơn vị: triệu đồng).
Lương | \(\left[ {10;15} \right)\) | \(\left[ {15;20} \right)\) | \(\left[ {20;25} \right)\) | \(\left[ {25;30} \right)\) | \(\left[ {30;35} \right)\) | \(\left[ {35;40} \right]\) |
|
Công ty A | 18 | 13 | 9 | 5 | 3 | 2 | \(n = 50\) |
Công ty B | 19 | 12 | 7 | 6 | 3 | 3 | \(n = 50\) |
a) Tính lương trung bình của hai công ty A, B? Công ty nào trả lương nhiều hơn?
b) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A và B. Công ty nào có mức lương đồng đều hơn?