Đề kiểm tra Hệ thức lượng trong tam giác (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho \(\Delta ABC\)có \(a = 2\), \(b = 6\), \(\widehat C = {153^{\rm{o}}}\). Diện tích của tam giác là
\(4\).
\(6\sqrt 2 \).
\(3\sqrt 2 \).
\(4\sqrt 2 \).
Cho tam giác ABC có ba cạnh \(a = 5,\;b = 6,\;c = 7\). Tính côsin góc\(A\).
\(\frac{5}{7}\).
\(\frac{2}{{21}}\).
\(\frac{{55}}{{42}}\).
\(\frac{{10}}{7}\).
Cho tam giác ABC có các cạnh \(BC = a = 6\,cm\), \(AC = b = 7\,cm\), \(AB = c = 5\,cm\). Tính \(\cos B\)
\(\cos B = \frac{1}{5}\).
\(\cos B = \frac{{19}}{{35}}\).
\(\cos B = \frac{1}{{15}}\).
\(\cos B = \frac{5}{7}\).
Cho tam giác ABC có ba cạnh a=5 ; b=6; c=7 . Tính côsin góc A.
.
.
.
.
Tam giác có độ dài ba cạnh lần lượt là \(9\), \(10\), \(11\) có diện tích bằng:
\(15\sqrt 2 \).
\(30\sqrt 2 \).
\(50\sqrt 3 \).
\(25\sqrt 3 \).
Tam giác ABC có \(\widehat B = {135^0}\,,\,BC = 3\,,\,AB = \sqrt 2 \). Tính cạnh \(AC\).
\(\sqrt 5 \).
\(2,25\).
\(5\).
\(\sqrt {17} \).
Cho tam giác ABC có \[BC = 10\] và góc \[\widehat A = {30^0}\]. Bán kính \[R\] của đường tròn ngoại tiếp tam giác ABC bằng
\[R = 5\].
\[R = 10\sqrt 3 \].
\[R = 10\].
\[R = \frac{{10}}{{\sqrt 3 }}\].
Cho \(\Delta ABC\)có \(a = 6,b = 8,c = 10.\) Diện tích \(S\) của tam giác trên là:
\(48.\)
\(24.\)
\(12.\)
\(30.\)
Tính chu vi tam giác ABC biết rằng \(AB = 6\) và \(2\sin A = 3\sin B = 4\sin C\).
\(10\sqrt 6 .\).
\(26.\).
\(13.\).
\(5\sqrt {26} .\)
Tam giác ABC có \(\widehat A = {68^0}12'\), \(\widehat B = {34^0}44'\), \(AB = 117.\) Tính \(AC\)?
\(68.\)
\(168.\)
\(118.\)
\(200.\)
Cho tam giác ABC. Biết \(AB = 2\); \(BC = 3\) và \(\widehat {ABC} = 60^\circ \). Tính chu vi và diện tích tam giác \(ABC\).
\(5 + \sqrt 7 \)và \(\frac{3}{2}\).
\(5 + \sqrt 7 \)và \(\frac{{3\sqrt 3 }}{2}\).
\(5\sqrt 7 \)và \(\frac{{3\sqrt 3 }}{2}\).
\(5 + \sqrt {19} \)và \(\frac{3}{2}\).
Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\) của ngọn núi. Biết rằng độ cao \(AB\) bằng \(70m\), phương nhìn \(AC\) tạo với phương nằm ngang góc \(30^\circ \). Phương nhìn \(BC\) tạo với phương nằm ngang góc \(15^\circ 30'\). Khi đó chiều cao của ngọn núi so với mặt đất (làm tròn đến hàng đơn vị) bằng
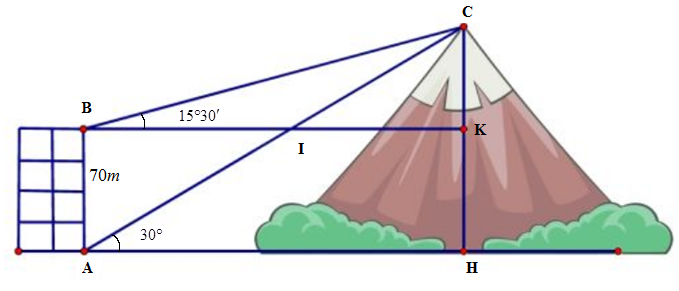
\(135m\).
\(133m\).
\(136m\).
\(134m\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác ABC biết Khi đó:
a) \({c^2} = {a^2} + {b^2} - 2ab\cos C\)
b) \(c \approx 3,05(\;cm)\)
c) \(\cos A \approx 0,68\)
d)
Cho tam giác ABC có \(BC = a,CA = b,AB = c\). Khi đó:
a) \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
b) Góc \(A\) vuông khi và chỉ khi \({a^2} = {b^2} + {c^2}\);
b) Góc \(A\) nhọn khi và chỉ khi \({a^2} > {b^2} + {c^2}\);
c) Góc \(A\) tù khi và chỉ khi \({a^2} < {b^2} + {c^2}\).
Cho \(\Delta ABC\) có và \(b = 12\). Khi đó:
a)
b) \(a = 12\sqrt 2 ;\)
c) \(c \approx 8,21;\)
d) \(R = 15\)
Cho tam giác ABC. Khi đó:
a) \(a = b\cos C + c\cos B\)
b) \(\sin A = \sin B\cos C + \sin C\cos B\)
c) \({h_a} = 2R\sin B\sin C\)
d) \({b^2} - {c^2} = a(b\cos C - c\cos B)\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho tam giác ABC, có \(AB = 8,AC = 9,BC = 10\). Một điểm \(M\) nằm trên cạnh \(BC\) sao cho \(BM = 7\). Tính độ dài đoạn thẳng \(AM\).
Cho \(\Delta ABC\) có . Tính chiều cao \(AH\) của \(\Delta ABC\)
Cho tam giác nhọn ABC có \(a = 3,b = 4\) và diện tích \(S = 3\sqrt 3 \). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác đó.
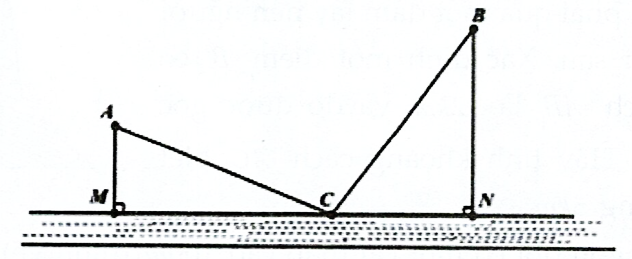
Thành phố Hải Đông dự định xây dựng một trạm nước sạch để cung cấp cho hai khu dân cư \(A\) và \(B\). Trạm nước sạch đặt tại vị trí \(C\) trên bờ sông. Biết \(AB = 3\sqrt {17} \;km\), khoảng cách từ \(A\) và \(B\) đến bờ sông lần lượt là \(AM = 3\;km,BN = 6\;km\) (hình vẽ). Gọi \(T\) là tổng độ dài đường ống từ trạm nước đến \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\).
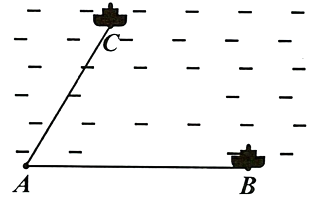
Hai chiếc tàu thuyền cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc 600. Tàu \(B\) chạy với tốc độ 20 hải lí một giờ. Tàu \(C\) chạy với tốc độ 15 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?\
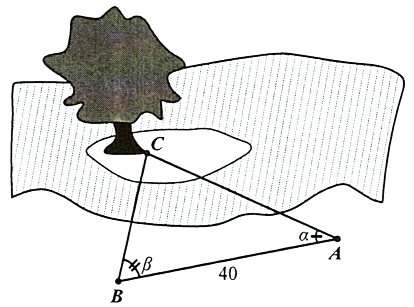
Để đo khoảng cách từ một điểm \(A\) trên bờ sông đến gốc cây \(C\) trên cù lao giữa sông, người ta chọn một điểm \(B\) cùng ở trên bờ với \(A\) sao cho từ \(A\) và \(B\) có thể nhìn thấy điểm \(C\). Ta đo được khoảng cách \(AB = 40\;m\), . Vậy sau khi đo đạc và tính toán khoảng cách \(AC\) bằng bao nhiêu mét?