Đề kiểm tra Hệ thức lượng trong tam giác (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho\(\Delta ABC\) có \(a = 4\), \(c = 5\), \(\widehat B = 150^\circ \). Tính diện tích tam giác ABC
\(S = 10\).
\(S = 10\sqrt 3 \).
\(S = 5\).
\(S = 5\sqrt 3 \).
Cho \[\Delta ABC\]có \[a = 2\]; \[b = 6\]; \[\widehat {C\,} = 135^\circ \]. Diện tích của tam giác là
\[6\sqrt 2 \].
\[3\sqrt 2 \].
\[4\sqrt 3 \].
\[4\].
Cho tam giác ABC có\[AB = 5\];\[BC = 7\]; \[AC = 8\]. Số đo góc \[A\] bằng
\(45^\circ \).
\(90^\circ \).
\(60^\circ \).
\(30^\circ \).
Cho\(\Delta ABC\)có \(AB = 4\); \(AC = 6\); \(\widehat A = 120^\circ \). Độ dài cạnh BC là
\(\sqrt {19} \).
\(3\sqrt {19} \).
\(2\sqrt {19} \).
\(2\sqrt 7 \).
Cho tam giác ABC có \(\widehat B = {60^0},AB = 10,BC = 6\). Tính độ dài cạnh \(AC\):
\(2\sqrt {19} \).
\(6\sqrt 2 \).
\(14\).
\(76\).
Tam giác \(ABC\)có \(\widehat {A\;} = 120^\circ \)thì câu nào sau đây đúng
\({a^2} = {b^2} + {c^2} + 3bc\).
\({a^2} = {b^2} + {c^2} - bc\).
\({a^2} = {b^2} + {c^2} - 3bc\).
\({a^2} = {b^2} + {c^2} + bc\).
Cho tam giác ABC có a=4 ; b=3 C= 60 độ .Tính độ dài cạnh c .
.
.
.
.
Cho tam giác ABC có \[AB = 5,\,BC = 7,\,CA = 8\]. Số đo góc \[A\] bằng
\[45^\circ \].
\[90^\circ \].
\[60^\circ \].
\[30^\circ \].
Cho tam giác ABC có \[BC = 10\] và góc\[A = {30^0}\]. Bán kính \[R\] của đường tròn ngoại tiếp tam giác ABC bằng
\[\frac{{10}}{{\sqrt 3 }}\].
\[5\].
\[10\sqrt 3 \].
\[10\].
Tam giác đều cạnh\(a\) nội tiếp trong đường tròn bán kính \(R\) bằng
\[\frac{{a\sqrt 3 }}{2}\].
\[\frac{{a\sqrt 3 }}{3}\].
\[\frac{{a\sqrt 2 }}{3}\].
\[\frac{{a\sqrt 3 }}{4}\].
Cho tam giác ABC có góc \(A = {30^0}\), góc \(B = {45^0}\). Tính \(\frac{{{h_a}}}{{{h_b}}}\).
\(\frac{{{h_a}}}{{{h_b}}} = \frac{1}{2}\).
\(\frac{{{h_a}}}{{{h_b}}} = \frac{1}{{2\sqrt 2 }}\).
\(\frac{{{h_a}}}{{{h_b}}} = \sqrt 2 \).
\(\frac{{{h_a}}}{{{h_b}}} = \frac{{\sqrt 2 }}{2}\).
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, \(\widehat {CAD} = {63^0}\); \(\widehat {CBD} = {48^0}\). Chiều cao h của khối tháp gần với giá trị nào sau đây?
61,4 m.
18,5 m.
60 m.
18 m.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác ABC có các cạnh \(a = 6\;m,b = 8\;m,c = 10\;m\). Khi đó:
a) \(p = 16\,(cm)\)
b) \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
c) \(S = 24\left( {\;c{m^2}} \right)\)
d) \(r = 4(\;cm)\)
Cho tam giác ABC có các cạnh \(a = 3\;cm,b = 4\;cm,c = 5\;cm\). Khi đó:
a) \(p = 12(\;cm)\)
b) \({S_{ABC}} = \sqrt {p(p - a)(p - b)(p - c)} \)
c) \({S_{ABC}} = 6\left( {\;c{m^2}} \right).\)
d) \[R = 3,5(\;cm)\]
Cho tam giác ABC biết cạnh . Khi đó:
a) \(\hat A = 40^\circ \)
b) \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = R\)
c) \(R \approx 106,96\;cm\)
d) \[b \approx 179,4\;cm\]
Cho \(\Delta ABC\) có \(BC = \sqrt 6 ,CA = 2,AB = 1 + \sqrt 3 \). Khi đó:
a)
b)
c) \(S = \frac{{3 + \sqrt 3 }}{2}\)
d) \(R = \sqrt 2 .\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình bình hành ABCD có và \(AB = 5,AD = 8\). Tính độ dài đường chéo \(AC\).
Cho tam giác ABC thỏa mãn \({h_a} = \sqrt {p(p - a)} \), trong đó \(a,b,c\) là ba cạnh, \({h_a}\) là chiều cao ứng với cạnh \(a\) của tam giác và \(p\) là nửa chu vi tam giác đó. Tam giác \(ABC\) là tam giác gì?
Cho hình thoi ABCD có cạnh bằng \(a\). Góc . Tính diện tích hình thoi ABCD.
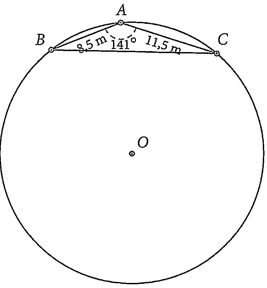
Để đo đường kính một hồ hình tròn, người ta làm như sau: Lấy ba điểm \(A,B,C\) như hình vẽ, sao cho \(AB = 8,5m;AC = 11,5m;\widehat {BAC} = 141^\circ \). Hãy tính đường kính của hồ nước đó.
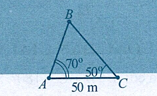
Để đo khoảng cách từ vị trí \(A\) trên bờ sông đến vị trí \(B\) của con tàu bị mắc cạn gần một cù lao giữa sông, bạn Minh đi dọc bờ sông từ vị trí \(A\) đến vị trí \(C\) cách \(A\) một khoảng bằng \(50\;m\) và đo các góc . (Hình). Tính khoảng cách \(AB\) theo đơn vị mét (làm tròn kết quả đến hàng đơn vị)
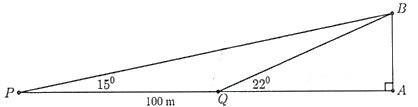
Hai chiếc tàu thủy \(P\) và \(Q\) cách nhau \(100\;m\). Từ \(P\) và \(Q\) thẳng hàng với chân \(A\) của tháp hải đăng \(AB\) ở trên bờ biển người ra nhìn chiêu cao \(AB\) của tháp dưới các góc và . Tính chiều cao \(AB\) của tháp?