Đề kiểm tra Hệ thức lượng trong tam giác (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tam giác ABC có \(\widehat A = 60^\circ \), \(b = 10\), \(c = 20\). Diện tích tam giác ABC bằng
\[70\sqrt 3 \].
\[60\sqrt 3 \].
\[50\sqrt 3 \].
\[40\sqrt 3 \].
Cho tam giác ABC có \(B = {135^0}\), \(AB = \sqrt 2 \) và \(BC = 3\). Độ dài cạnh \(AC\)bằng?
\(\sqrt 5 \).
\(\sqrt {17} \).
\(5\).
\(\frac{9}{4}\).
Cho tam giác \[\Delta ABC\] có \[AB = 9,BC = 8,\widehat {ABC} = {60^0}\]. Tính độ dài đoạn \[AC\].
\[\sqrt {113} \].
\[\sqrt {73} \].
\[\sqrt {217} \].
\[8\]
Cho \(\Delta ABC\)có \(BC = 12\,,\,AC = 15\), góc \(\widehat C = 60^\circ \). Khi đó độ dài cạnh \(AB\)là:
\(AB = 6\sqrt 7 \).
\(AB = 3\sqrt 7 \)
\(AB = 6\sqrt {21} \).
\(AB = 3\sqrt {21} \).
Tính góc \(C\) của tam giác ABC biết \({c^2} = {a^2} + {b^2} + ab\).
\(C = 150^\circ .\)
\(C = 120^\circ .\)
\(C = 60^\circ .\)
\(C = 30^\circ .\)
Cho tam giác ABC có Độ dài của cạnh \(BC\) có giá trị gần nhất với giá trị nào dưới đây
\(5,2.\).
\(2,5.\).
\(2,6.\).
\(9,8.\)
Cho \[\Delta ABC\] có \[AB = 5,\,\widehat {A\,} = 40^\circ ,\,\widehat {B\,} = 60^\circ \]. Độ dài \[BC\] gần nhất với kết quả nào?
\(3,1\).
\[3,7\].
\(3,5\).
\(3,8.\)
Cho tam giác ABC có \(BC = 5cm,\,\widehat {BAC} = {30^ \circ }\). Bán kính đường tròn ngoại tiếp tam giác ABC bằng
\(5cm\).
\(10cm\).
\(5\sqrt 3 cm\).
\(\frac{{5\sqrt 3 }}{3}cm\).
Cho tam giác ABC có \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và \(a = 10\). Tính chu vi tam giác đó.
\(24.\)
\(36.\)
\(22.\)
\(12.\)
Cho tam giác ABC có \(AB = 3,\;BC = 5\) và độ dài đường trung tuyến \(BM = \sqrt {13} \). Tính độ dài \(AC\).
\(\sqrt {11} \).
\(4\).
\(\frac{9}{2}\).
\(\sqrt {10} \).
Một người quan sát đứng cách một cái tháp \[10m\], nhìn thẳng cái tháp dưới một góc \[{55^ \circ }\] và được phân tích như trong hình. Tính chiều cao của tháp. 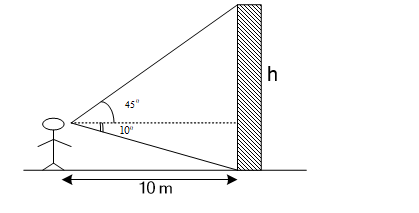
\[67{\rm{m}}\].
\[24{\rm{m}}\].
\[16{\rm{m}}\].
\[12{\rm{m}}\].
Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\)của ngọn núi. Biết rằng độ cao \(AB = 70{\rm{m}}\), phương nhìn \(AC\) tạo với phương nằm ngang góc\({30^0}\), phương nhìn \(BC\) tạo với phương nằm ngang góc \({15^0}30'\) (tham khảo hình vẽ). Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
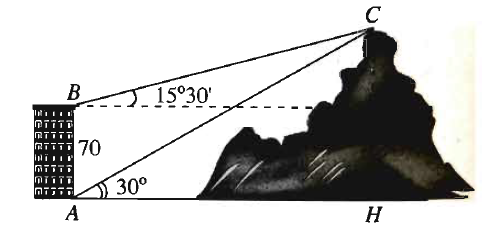
\(195{\rm{m}}\).
\(234{\rm{m}}\).
\(165{\rm{m}}\).
\(135{\rm{m}}\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác ABC có Khi đó:
a) \(a = \sqrt {127} \;cm\)
b) \(\cos C \approx 0,91\)
c) \(\cos B \approx 0,21\)
d) \(R \approx 6,03(\;cm)\)
Cho tam giác ABC biết các cạnh \(a = 52,1\;cm,b = 85\;cm,c = 54\;cm\). Khi đó:
a) \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
b) \(A \approx {32^0}\)
c)
d)
Cho tam giác ABC, biết \(b = 7,c = 5,\cos A = \frac{3}{5}\). Khi đó:
a) \(\sin A = \frac{4}{5}\)
b) \(S = 14\)
c) \(a = 3\sqrt 2 \)
d) \(r = 4 - \sqrt 2 \)
Cho \(\Delta ABC\) có \(AB = 3,AC = 4\;A\), diện tích \(S = 3\sqrt 3 \). Khi đó:
a) \(B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A\)
b) \(\sin A = - \frac{{\sqrt 3 }}{2}\)
c) \(\cos A = \frac{1}{2}\)
d) \(\cos A = - \frac{1}{2}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho tam giác \(ABC\) có . Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác.
Cho tam giác ABC có \(a = 7\;cm,b = 8\)\(c = 6cm.\) Hãy tính độ dài đường trung tuyến \({m_a}\) của tam giác đã cho.?
Cho tam giác ABC có \(AB = 4,AC = 10\) và đường trung tuyến \(AM = 6\). Tính độ dài cạnh \(BC\)?
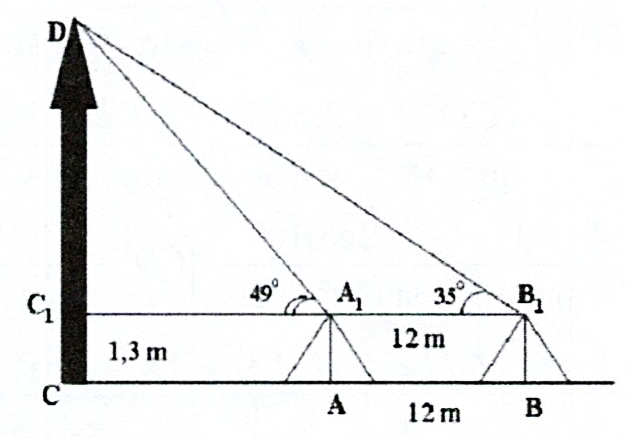
Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12\;m\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3\;m\). Gọi \(D\) là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao \(CD\) của tháp. Người ta đo được góc và . Tính chiều cao \(CD\) của tháp.
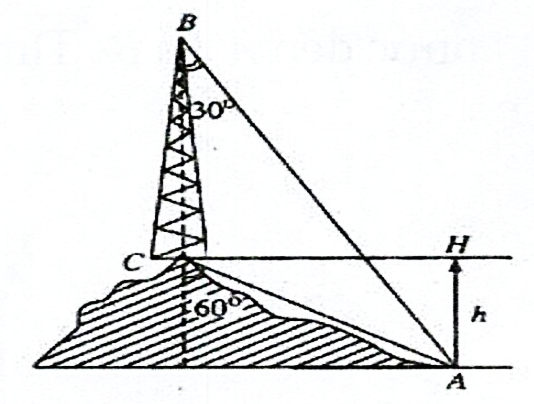
Trên ngọn đồi có một cái tháp cao \(100\;m\) (hình vẽ). Đỉnh tháp \(B\) và chân tháp \(C\) lần lượt nhìn điểm \(A\) ở chân đồi dưới các góc tương ứng bằng và so với phương thẳng đứng. Tính chiều cao \(AH\) của ngọn đồi.
Hai chiếc tàu thủy cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc 600. Tàu thứ nhất chạy với tốc độ \(20\;km/h\), tàu thứ hai chạy với tốc độ \(30\;km/h\). Hỏi sau 3 giờ hai tàu cách nhau bao nhiêu km?








