Đề kiểm tra Hàm số lượng giác (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Tập xác định của hàm số \(y = \frac{{1 - \sin x}}{{\cos x}}\) là:
\(\mathbb{R}\backslash \left\{ { - \frac{\pi }{2} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \{ k\pi \left| {k \in \mathbb{Z}} \right.\} \).
Trên khoảng nào sau đây thì hàm số \(y = \cos x\) đồng biến?
\(\left( { - \pi ;0} \right)\).
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
\(\left( {0;\pi } \right)\).
\(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Hàm số nào sau đây đồng biến trên khoảng \[\left( {\frac{\pi }{2};\pi } \right)\]?
\(y = \cos x\).
\(y = \tan x\).
\(y = \cot x\).
\(y = \sin x\).
Hàm số nào sau đây là hàm số chẵn trên \(\mathbb{R}\)?
\(y = x.\cos 2x\).
\(y = \left( {{x^2} + 1} \right).\sin x\).
\(y = \frac{{\cos x}}{{1 + {x^2}}}\).
\(y = \frac{{\tan x}}{{1 + {x^2}}}\).
Tập giá trị của hàm số \(y = 4\sin x\) là
\(\left[ { - 1;1} \right]\).
\(\left[ { - 2;2} \right]\).
\(\left[ { - 6;6} \right]\).
\(\left[ { - 4;4} \right]\).
Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó?
\(y = \frac{{\sin x}}{{1 - \sin x}}\).
\(y = \frac{{{{\sin }^2}x}}{{1 + \cos x}}\).
\(y = \frac{{\cos x}}{{x + {x^2}}}\).
\(y = \frac{{\tan x}}{{1 + {{\sin }^2}x}}\).
Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
\(y = \tan x\).
\(y = x\cot x\).
\(y = x\sin x\).
\(y = \frac{1}{x}\).
Tập giá trị của hàm số \(y = 2\sin 2x + 3\) là
\(\left[ {1;5} \right]\).
\(\left[ { - 2;3} \right]\).
\(\left[ {2;3} \right]\).
\(\left[ {0;1} \right]\).
Tập xác định của hàm số \(y = - \tan x\) là:
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\).
Hàm số nào sau đây là hàm số lẽ trên tập xác định của nó?
\[y = \cos x.\]
\[y = x\sin x.\]
\[y = - \sin x\cos 2x.\]
\[y = {\sin ^2}x.\]
Số giá trị \(\alpha \in [ - \pi ;2\pi ]\) sao cho \(\cos \alpha = \frac{1}{3}\) là:
1.
2.
3.
4.
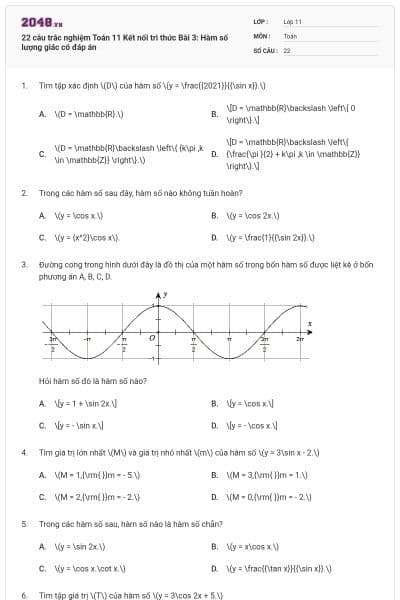
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án \(A,\;B,\;C,\;D\).
Hỏi hàm số đó là hàm số nào?
\(y = \sin \frac{x}{2}\).
\(y = \cos \frac{x}{2}\).
\(y = - \cos \frac{x}{4}\).
\(y = \sin \left( { - \frac{x}{2}} \right)\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f(x) = \tan 2x - 1\). Khi đó:
a) Giá trị của hàm số tại \(x = \frac{\pi }{8}\) bằng 0
b) Giá trị của hàm số tại \(x = \frac{\pi }{3}\) bằng \( - \sqrt 3 - 1\)
c) Có ba giá trị \(x\) thuộc \([0;\pi ]\) khi hàm số đạt giá trị bằng \[ - 2\].
d) Hàm số đã cho là hàm tuần hoàn.
Tìm được tập xác định của hàm số. Khi đó:
a) Hàm số \(y = \cot \left( {3x - \frac{\pi }{4}} \right)\) xác định khi \(x \ne \frac{\pi }{{12}} + \frac{{k\pi }}{3}(k \in \mathbb{Z})\)
b) Hàm số \(y = \sqrt {\sin x - 1} \) có tập xác định là \(D = \mathbb{R}\)
c) Hàm số \(y = \frac{{\sin x}}{{2 - \cos x}}\) có tập xác định là \(D = \mathbb{R}\)
d) Hàm số \(y = \tan 2x + \cot 2x\) xác định khi \(\left\{ {\begin{array}{*{20}{l}}{\cos 2x \ne 0}\\{\sin 2x \ne 0}\end{array}} \right.\)
Cho hàm số \(y = 3 - \sin \left( {2x + \frac{\pi }{4}} \right)\), khi đó:
a) Hàm số có tập xác định \(D = \mathbb{R}\).
b) Giá trị nhỏ nhất của hàm số bằng 2
c) Giá trị lớn nhất của hàm số bằng 4
d) Tập giá trị của hàm số là \(T = [2;4]\)
Chiều cao so với mực nước biển trung bình tại thời điểm \(t\) (giây) của mỗi cơn sóng được cho bởi hàm số \(h(t) = 75\sin \left( {\frac{{\pi t}}{8}} \right)\), trong đó \(h(t)\) được tính bằng centimét.
a) Chiều cao của sóng tại các thời điểm 5 giây bằng \(69,3(\;cm)\)
b) Chiều cao của sóng tại các thời điểm 20 giây bằng \(75(\;cm)\)
c) Trong 30 giây đầu tiên (kể từ mốc \(t = 0\) giây), thời điểm để sóng đạt chiều cao lớn nhất 6 giây
d) Trong 30 giây đầu tiên (kể từ mốc \(t = 0\) giây), thời điểm để sóng đạt chiều cao lớn nhất 18 giây
(Tất cả kết quả được làm tròn đến hàng phần mười)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm chu kỳ của hàm số \(y = \sin 3x + 3\cos 2x\).
Xét tính chẵn, lẻ của hàm số \(g(x) = \frac{1}{x}\).
Tìm tập giá trị của hàm số: \(y = \sin x + \sqrt 3 \cos x + 3\);
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số: \(y = 2 + 2\cos x + {\cos ^2}x\)
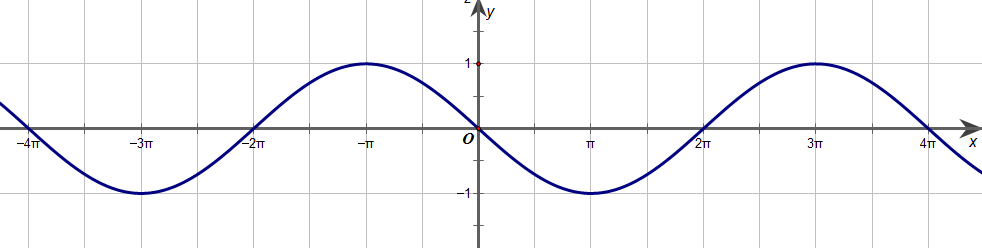
Trong Hinh 13, một chiếc máy bay \(A\) bay ờ độ cao \(500{\rm{\;m}}\) theo một đường thẳng đi ngang qua phía trên trạm quan sát \(T\) ở mặt đất. Hinh chiếu vuông góc của \(A\) lên mặt đất là \(H,\alpha \) là góc lượng giác \(\left( {Tx,TA} \right)(0 < \alpha < \pi )\).
Biểu diễn tọa độ \({x_H}\) của điềm \(H\) trên trục \(Tx\) theo \(\alpha \).và dựa vào đồ thị hàm số côtang, hãy cho biết với \(\frac{\pi }{6} < \alpha < \frac{{2\pi }}{3}\) thì \({x_H}\) nằm trong khoảng nào.
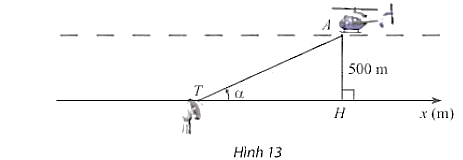
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng \(3{\rm{\;m}}\). Xét gàu \(G\) của guồng. Ban đầu gàu \(G\) nằm ở vị trí \(A\) (Hinh 12\()\).
a) Viết hàm số \(h\) biểu diễn chiều cao (tính bằng mét) của gàu \(G\) so với mặt nước theo góc \(\alpha = \left( {OA,OG} \right)\).
b) Guồng nước quay hết mỗi vòng trong 30 giây. Dựa vào đồ thị của hàm số \(\sin \), hãy cho biết ở các thời điềm \(t\) nào trong 1 phút đầu, khoảng cách của gàu đến mặt nước bằng \(1,5{\rm{\;m}}\).