Đề kiểm tra Hàm số lượng giác (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Tập xác định của hàm số \(y = \sqrt {\frac{{1 - \cos x}}{{1 + \sin x}}} \) là:
\(\mathbb{R}\).
\(\emptyset \).
\(\mathbb{R}\backslash \left\{ { - \frac{\pi }{2} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
Tập xác định của hàm số \(y = \tan x + \frac{1}{{1 + {{\cot }^2}x}}\) là:
\(\mathbb{R}\backslash \left\{ {k\frac{\pi }{2}\left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \left\{ { - \frac{\pi }{4} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
\(\mathbb{R}\backslash \left\{ { - \frac{\pi }{4} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
Hàm số nào trong các hàm số sau đồng biến trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)?
\(y = \sin x\).
\(y = \cos x\).
\(y = \tan x\).
\(y = \cot x\).
Tìm tập xác định của hàm số \(y = \frac{{1 - \sin x}}{{\cos x}}\)
\(x \ne \frac{\pi }{2} + k\pi \).
\(x \ne - \frac{\pi }{2} + k2\pi \).
\(x \ne \frac{\pi }{2} + k2\pi \).
\(x \ne k\pi \).
Hàm số nào sau đây nghịch biến trên \(\left( {\frac{\pi }{2};\pi } \right)\)?
\(y = - \sin x\).
\(y = \cos x\).
\(y = - \cot x\).
\(y = \tan x\).
Hàm số nào sau đây đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\)?
\(y = \sin x\).
\(y = \cos x\).
\(y = \tan x\).
\(y = \cot x\).
Khẳng định nào dưới đây là sai?
Hàm số \[y = \cos x\] là hàm số lẻ.
Hàm số \[y = \cot x\] là hàm số lẻ.
Hàm số \[y = \sin x\] là hàm số lẻ.
Hàm số \[y = \tan x\] là hàm số lẻ.
Chọn khẳng định sai về tính chẵn, lẻ của hàm số.
Hàm số \(y = \cot x\) là hàm lẻ.
Hàm số \(y = \sin x\) là hàm lẻ.
Hàm số \[y = \cos x\] là hàm chẵn.
Hàm số \(y = \tan x\) là hàm chẵn.
Trong các hàm số sau, hàm số nào là hàm số chẵn trên \(\mathbb{R}\)?
\(y = \sin \left( {\frac{\pi }{2} - x} \right)\).
\(y = \tan x\).
\(y = \sin x\).
\(y = \sin \left( {x + \frac{\pi }{6}} \right)\).
Hàm số \(y = 3 - 5\sin x\) có giá trị lớn nhất bằng
\(2.\)
\(4.\)
\(6.\)
\(8.\)
Giá trị nhỏ nhất của hàm số \(y = 2\sin x + 5\) là
\(3\).
\(2\).
\(5\).
\(4\).
Cho đồ thị hàm số \(f\left( x \right)\) như hình vẽ dưới đây. Hỏi tịnh tiến đồ thị hàm số \(f\left( x \right)\) theo vectơ \(\vec v = \left( {\frac{\pi }{2};0} \right)\) thì được đồ thị hàm số
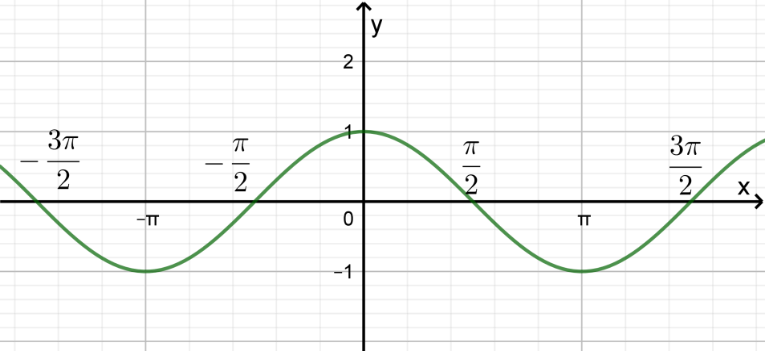
\(y = \tan x\).
\(y = \sin x\).
\(y = \cos x\).
\(y = \cot x\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f(x) = |x|\sin x\). Khi đó:
a) Tập xác định của hàm số: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
b) \(f( - \pi ) = - f(\pi )\)
c) Hàm số đã cho đối xứng qua gốc tọa độ \(O\left( {0;0} \right)\)
d) \(f( - x) = - f(x)\)
Cho hàm số \(f(x) = |\tan x| + \left| {{x^3} - 3x} \right|\). Khi đó:
a) Tập xác định của hàm số: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
b) \(f( - \pi ) = - f(\pi ){\rm{. }}\)
c) Hàm số đã cho đối xứng qua gốc tọa độ \(O\left( {0;0} \right)\)
d) Hàm số đã cho là hàm số chẵn.
Tìm được tập giá trị các hàm số sau trên tập xác định của chúng:
a) Hàm số \(y = 3\sin x\) có tập giá trị là \(T = [ - 3;3]\).
b) Hàm số \(y = 2\cos x - 1\)có tập giá trị là \(T = [ - 3;1]\).
c) Hàm số \(y = 2030 - 4\cos x\)có tập giá trị là \(T = [2026;2034]\).
d) Hàm số \(y = {\sin ^2}x + 4\sin x - 1\)có tập giá trị là \(T = [ - 3;3]\).
Cho hàm số \(f(x) = \tan x\) và \(g(x) = {\cot ^2}x - \frac{{\sin 2x}}{2}\). Khi đó:
a) Tập xác định hàm số \(f\left( x \right)\): \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
b) Hàm số \(f\left( x \right)\) là hàm không tuần hoàn.
c) Tập xác định hàm số \(g\left( x \right)\): \(D = \mathbb{R}\backslash \{ k\pi \left| {k \in \mathbb{Z}} \right.\} \).
d) Hàm số \(g\left( x \right)\) là hàm tuần hoàn.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm tập giá trị của hàm số: \(y = {\sin ^6}x + {\cos ^6}x\)
Tìm tập giá trị của hàm số \(y = \frac{{2\sin x + \cos x}}{{\sin x + 2\cos x + 4}}\).
Xét tính chẵn, lẻ của hàm số sau: \(y = {\sin ^2}x + \cos x\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số: \(y = \sqrt {1 + \sin x} - 3\).
Tìm giá trị nguyên của tham số \(m\) để hàm số \(y = \sqrt {\frac{{m - 1}}{m} - 2\cos 4x} \) xác định trên \(\mathbb{R}\).
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin \(M\) phụ thuộc vào góc lượng giác \(\alpha = \left( {Ox,OM} \right)\) theo hàm số \({v_x} = 0,3{\rm{sin}}\alpha \left( {{\rm{m}}/{\rm{s}}} \right)\) (Hình 11\()\).
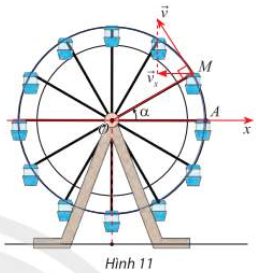
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của \({v_{{x^{\rm{*}}}}}\)
b) Dựa vào đồ thị của hàm số \(\sin \), hãy cho biết trong vòng quay đầu tiên \(\left( {0 \le \alpha \le 2\pi } \right)\), góc \(\alpha \) ở trong các khoảng nào thì \({v_x}\) tăng.