22 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác có đáp án
22 câu hỏi
Tìm tập xác định \(D\) của hàm số \(y = \frac{{2021}}{{\sin x}}.\)
\(D = \mathbb{R}.\)
\[D = \mathbb{R}\backslash \left\{ 0 \right\}.\]
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\]
Trong các hàm số sau đây, hàm số nào không tuần hoàn?
\(y = \cos x.\)
\(y = \cos 2x.\)
\(y = {x^2}\cos x\).
\(y = \frac{1}{{\sin 2x}}.\)
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
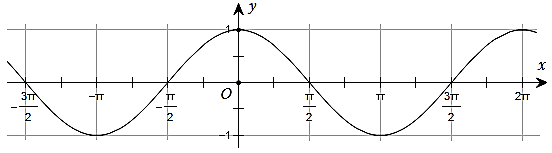
Hỏi hàm số đó là hàm số nào?
\[y = 1 + \sin 2x.\]
\[y = \cos x.\]
\[y = - \sin x.\]
\[y = - \cos x.\]
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = 3\sin x - 2.\)
\(M = 1,{\rm{ }}m = - 5.\)
\(M = 3,{\rm{ }}m = 1.\)
\(M = 2,{\rm{ }}m = - 2.\)
\(M = 0,{\rm{ }}m = - 2.\)
Trong các hàm số sau, hàm số nào là hàm số chẵn?
\(y = \sin 2x.\)
\(y = x\cos x.\)
\(y = \cos x.\cot x.\)
\(y = \frac{{\tan x}}{{\sin x}}.\)
Tìm tập giá trị \(T\) của hàm số \(y = 3\cos 2x + 5.\)
\(T = \left[ { - 1;1} \right].\)
\(T = \left[ { - 1;11} \right].\)
\(T = \left[ {2;8} \right].\)
\(T = \left[ {5;8} \right].\)
Hàm số \(y = 5 + 4\sin 2x\cos 2x\) có tất cả bao nhiêu giá trị nguyên?
\(3.\)
\(4.\)
\(5.\)
\(6.\)
Gọi \(M,{\rm{ }}m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sin x + \cos x\). Tính \(P = M - m.\)
\(P = 4.\)
\(P = 2\sqrt 2 .\)
\(P = \sqrt 2 .\)
\(P = 2.\)
Tìm chu kì \(T\) của hàm số \(y = \cos 2x + \sin \frac{x}{2}.\)
\(T = 4\pi .\)
\(T = \pi .\)
\(T = 2\pi .\)
\(T = \frac{\pi }{2}.\)
Tìm chu kì \(T\) của hàm số \[y = \cos 3x + \cos 5x.\]
\(T = \pi .\)
\(T = 3\pi .\)
\(T = 2\pi .\)
\(T = 5\pi .\)
Hàm số nào sau đây có chu kì khác \(\pi \)?
\(y = \sin \left( {\frac{\pi }{3} - 2x} \right).\)
\(y = \cos 2\left( {x + \frac{\pi }{4}} \right).\)
\(y = \tan \left( { - 2x + 1} \right).\)
\(y = \cos x\sin x.\)
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
\(y = \frac{1}{{{{\sin }^3}x}}.\)
\(y = \sin \left( {x + \frac{\pi }{4}} \right).\)
\(y = \sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right).\)
\(y = \sqrt {\sin 2x} .\)
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(f\left( x \right) = \tan 2x - 1\).
a) Giá trị của hàm số \(f\left( x \right)\) tại \(x = \frac{\pi }{8}\) bằng 0.
b) Hàm số \(f\left( x \right)\) là hàm số chẵn.
c) Tập xác định của hàm số \(f\left( x \right)\) là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\) và tập giá trị là \[\mathbb{R}.\]
d) Hàm số \(f\left( x \right)\) là hàm tuần hoàn.
Cho hàm số \(f\left( x \right) = {\sin ^2}x + \cos x - 1\).
a) Tập xác định của hàm số \(D = \mathbb{R}\).
b) \(f\left( { - \pi } \right) = - f\left( \pi \right)\).
c) \(f\left( { - x} \right) = f\left( x \right)\).
d) Hàm số đã cho là hàm số chẵn.
Chiều cao so với mực nước biển trung bình tại thời điểm \(t\) (giây) của mỗi cơn sóng được cho bởi hàm số \(h\left( t \right) = 75\sin \left( {\frac{{\pi t}}{8}} \right)\), trong đó \(h\left( t \right)\) được tính bằng centimét.
a) Chiều cao của sóng tại các thời điểm 5 giây bằng \(69,3\,\,{\rm{(cm)}}\).
b) Chiều cao của sóng tại các thời điểm 20 giây bằng \(75\,\,{\rm{(cm)}}\).
c) Trong 30 giây đầu tiên (kể từ mốc \(t = 0\) giây), thời điểm để sóng đạt chiều cao lớn nhất 6 giây.
d) Trong 30 giây đầu tiên (kể từ mốc \(t = 0\) giây), thời điểm để sóng đạt chiều cao lớn nhất 18 giây.
(Tất cả kết quả được làm tròn đến hàng phần mười)
Cho hàm số \(y = 3 - \sin \left( {2x + \frac{\pi }{4}} \right)\).
a) Hàm số có tập xác định \(D = \mathbb{R}\).
b) Giá trị nhỏ nhất của hàm số bằng 2.
c) Giá trị lớn nhất của hàm số bằng 4.
d) Tập giá trị của hàm số là \(T = \left[ {2\,;4} \right]\).
Hai điểm sáng M và N cùng dao động điều hòa trên trục Ox với phương trình lần lượt là \({x_M} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{{2\pi }}{3}} \right)\,\,{\rm{cm}}\) và \({x_N} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{\pi }{3}} \right)\,\,{\rm{cm}}\).
a) Biên độ dao động tổng hợp của hai điểm sáng M và N là \(4\sqrt 2 .\)
b) Khoảng cách của M và N dao động với phương trình là \(4\sqrt 3 \cos \left( {\frac{{5\pi }}{3}t + \pi } \right)\).
c) Khoảng cách lớn nhất của M và N trong quá trình chúng dao động là \(4.\)
d) Kể từ \(t = 0\), thời điểm M và N gặp nhau lần thứ 2025 là \(1211,8\)s.
PHẦN III. TRẢ LỜI NGẮN
Biết tập giá trị của hàm số \(y = 5 + 4\sin 2x\cos 2x\) là \(T = \left[ {a\,;b} \right]\). Tính \(a + b\).
Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{2\sin x + 3\cos x + 1}}{{\sin x - \cos x + 2}}\).
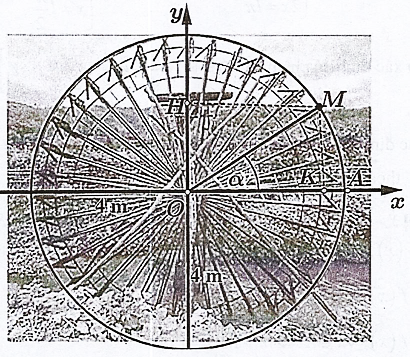
Một cái guồng nước có vành kim loại ngoài cùng là một đường tròn tâm \(O\), bán kính là \(4\;{\rm{m}}\). Xét chất điểm \(M\) thuộc đường tròn đó và góc \[\alpha = \left( {OA,OM} \right)\]. Giả sử mực nước lúc đang xét là tiếp xúc với đường tròn \(\left( {O\,;4} \right)\) và guồng nước quay theo chiều dương (ngược chiều kim đồng hồ). Biết rằng guồng nước quay hết một vòng sau 40 giây \((t = 0\) giây khi điểm \(M\) trùng \(A\)). Hỏi thời điểm bao nhiêu giây (trong 1 vòng quay đầu tiên) thì điểm \(M\) ở vị trí cao nhất so với mặt nước?
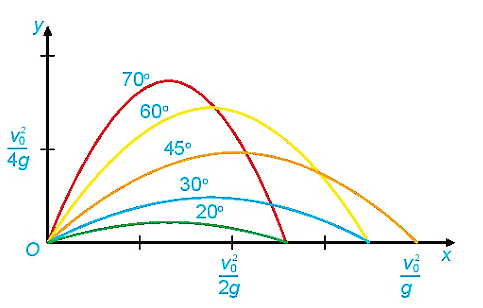
Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu \({v_0} = 500\;\,{\rm{m/s}}\) hợp với phương ngang một góc \(\alpha \) (đơn vị độ). Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \), ở đó \(g = 9,8\;\,{\rm{m/}}{{\rm{s}}^2}\) là gia tốc trọng trường. Biết rằng, để quả đạn đạt độ cao lớn nhất thì góc bắn là \(\alpha \). Giá trị của \(\alpha \) (đơn vị độ) là?
Giả sử nhiệt độ bên trong một căn phòng sau \(t\) giờ với \(0 \le t \le 12\) kể từ 12 giờ trưa được tính theo công thức \(T\left( t \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi t}}{6}} \right) + 26\). Biết rằng tập giá trị \(G\) của hàm số \(T\left( t \right)\) có dạng là \(\left[ {a;b} \right].\) Hãy tính \(P = a + b.\)