Đề kiểm tra Hàm số lượng giác (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Tập xác định của hàm số \(y = \sqrt {1 + \cos 2x} \) là:
\(\emptyset \).
\(\mathbb{R}\).
\([ - 1; + \infty )\).
\(\left[ { - \frac{1}{2}; + \infty } \right)\).
Hàm số nào sau đây là hàm số chẵn?
\(y = \cos x + 5\).
\(y = \tan x + \cot x\).
\(y = \sin ( - x)\).
\(y = \sin x - \cos x\).
Hàm số \(y = \cos x\) nghịch biến trên khoảng:
\((0;\pi )\).
\((\pi ;2\pi )\).
\(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
\(( - \pi ;0)\).
Tìm mệnh đề đúng.
Hàm số \(y = \cot x\) đồng biến trên khoảng \(\left( {0;\pi } \right)\).
Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( {\pi ;2\pi } \right)\).
Hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Chọn khẳng định sai.
Hàm số \[y = \tan \,x + \sin \,x\] là hàm số tuần hoàn với chu kì \(2\pi .\)
Hàm số \[y = \cos \,x\] là hàm số tuần hoàn với chu kì \(2\pi .\)
Hàm số \[y = \cot x + \tan x\] là hàm số tuần hoàn với chu kì \(\pi .\)
Hàm số \[y = \sin \,x\] là hàm số tuần hoàn với chu kì \(\pi .\)
Khẳng định nào sau đây đúng?
\(y = \sin x\) là hàm số nghịch biến trên \(\left( { - \frac{\pi }{4}\,;\,\frac{\pi }{4}} \right)\).
\(y = \cos x\) là hàm số nghịch biến trên \(\left( {\frac{\pi }{4}\,;\,\frac{{3\pi }}{4}} \right)\).
\(y = \sin x\) là hàm số nghịch biến trên \(\left( {0\,;\,\frac{{2\pi }}{3}} \right)\).
\(y = \tan x\) là hàm số nghịch biến trên \(\left( {\frac{\pi }{4}\,;\,\frac{{3\pi }}{4}} \right)\).
Với \(x \in \left( {0;\frac{\pi }{4}} \right)\), mệnh đề nào sau đây là đúng?
Cả hai hàm số \(y = - \sin 2x\) và \(y = - 1 + \cos 2x\) đều nghịch biến.
Cả hai hàm số \(y = - \sin 2x\) và \(y = - 1 + \cos 2x\) đều đồng biến.
Hàm số \(y = - \sin 2x\)nghịch biến, hàm số \(y = - 1 + \cos 2x\) đồng biến.
Hàm số \(y = - \sin 2x\) đồng biến, hàm số \(y = - 1 + \cos 2x\) nghịch biến.
Trong các hàm số sau, hàm số nào là hàm số chẵn?
\(y = x.\sin x\).
\(y = \tan x\).
\(y = 1 - \sin x\).
\(y = \cos x.\sin x\).
Tìm tập xác định của hàm số \(y = \frac{{\tan x}}{{\sin x - 1}}?\)
\(\mathbb{R}.\)
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \,,\,k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \,,\,k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k\pi \,,\,k \in \mathbb{Z}} \right\}\).
Tìm tập xác định của hàm số \[y = \sqrt {1 - \cos x} + \cot x\]?
\(\mathbb{R}\backslash \left\{ {k\pi ;k \in \mathbb{Z}} \right\}\).
\(\left( { - \infty ;1} \right]\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ;k \in \mathbb{Z}} \right\}\).
\(\left[ { - 1;1} \right]\backslash \left\{ 0 \right\}\).
Xét hàm số \(y = \cos x\) với \(x \in \left[ { - \pi ;\pi } \right].\) Khẳng định nào sau đây đúng?
Hàm số nghịch biến trên \(\left( { - \pi ;0} \right)\) và đồng biến trên \(\left( {0;\pi } \right)\).
Hàm số nghịch biến trên \(\left( { - \pi ;0} \right)\) và \(\left( {0;\pi } \right)\).
Hàm số đồng biến trên \(\left( { - \pi ;0} \right)\) và ngịch biến trên \(\left( {0;\pi } \right)\).
Hàm số đồng biến trên \(\left( { - \pi ;0} \right)\) và \(\left( {0;\pi } \right)\).
Cho hàm số \(y = \sin x\). Mệnh đề nào sau đây là đúng?
Hàm số đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\), nghịch biến trên khoảng \(\left( {\pi ;\frac{{3\pi }}{2}} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\), nghịch biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Hàm số đồng biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\), nghịch biến trên khoảng \(\left( { - \frac{\pi }{2};0} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f(x) = \tan x - x\). Khi đó:
a) Tập xác định của hàm số: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \mid \,k \in \mathbb{Z}} \right\}\).
b) \(f(\frac{\pi }{3}) = f( - \frac{\pi }{3})\)
c) \(f( - x) = - f(x)\)
d) Hàm số đối xứng với nhau qua trục\(Oy\)
Cho hàm số \(f(x) = 2\cos x + 1\) và \(g(x) = \sin x + \tan x\). Khi đó:
a) Tập xác định hàm số \(f\left( x \right)\): \(D = \mathbb{R}\).
b) Hàm số \(f\left( x \right)\) là hàm tuần hoàn.
c) Tập xác định hàm số \(g\left( x \right)\): \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{3} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
d) Hàm số \(g\left( x \right)\) là hàm không tuần hoàn.
Cho các hàm số sau: \(f(x) = 3{\sin ^3}x\); \(g(x) = - 5\cos \left( {2x + \frac{\pi }{3}} \right)\). Khi đó:
a) Tập xác định hàm số \(f\left( x \right)\) là: \(D = \mathbb{R}\).
b) Hàm số \(f\left( x \right)\) đã cho là hàm số chẵn.
c) Tập xác định hàm số \(g\left( x \right)\) là: \(D = \mathbb{R}\).
d) Hàm số \(g\left( x \right)\) đã cho là hàm số lẻ.
Tìm được tập xác định của các hàm số sau. Khi đó:
a) Hàm số \(y = \tan \left( {2x - \frac{\pi }{6}} \right)\) xác định khi: \(x \ne \frac{\pi }{3} + k\frac{\pi }{2}(k \in \mathbb{Z})\)
b) Hàm số \(y = \cot \left( {x + \frac{\pi }{3}} \right)\) xác định khi: \( \Leftrightarrow x + \frac{\pi }{3} \ne k\pi (k \in \mathbb{Z})\)
c) Hàm số \(y = \frac{{1 - \cos x}}{{\sin x}}\) có tập xác định là \(D = \mathbb{R}\backslash \{ 2k\pi \left| {k \in \mathbb{Z}} \right.\} \)
d) Hàm số \(y = \frac{{\tan 3x}}{{\cos x}}\) có tập xác định là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{8} + k\frac{\pi }{3}\left| {k \in \mathbb{Z}} \right.} \right\}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm tập giá trị của hàm số: \(y = 5 + 4\sin 2x\cos 2x\)
Xét tính chẵn, lẻ của hàm số sau: \(y = \tan x + 2\sin x\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số: \(y = 2\cos \left( {x - \frac{\pi }{3}} \right) - 1\).
Tìm \(x\) để hàm số \(y = 1 - 3\sqrt {1 - {{\cos }^2}x} \) đạt giá trị nhỏ nhất.
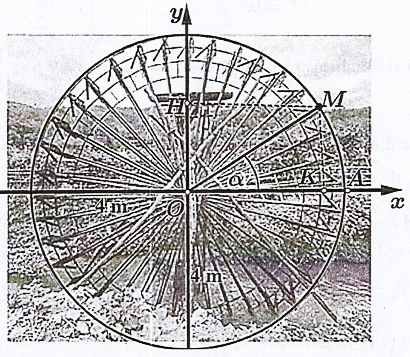
Một cái guồng nước có vành kim loại ngoài cùng là một đường tròn tâm \(O\), bán kính là \(4\;m\). Xét chất điểm \(M\) thuộc đường tròn đó và góc \(\alpha = (OA,OM)\).
Giả sử mực nước lúc đang xét là tiếp xúc với đường tròn \((O;4)\) và guồng nước quay theo chiều dương (ngược chiều kim đồng hồ).
Biết rằng guồng nước quay hết một vòng sau 40 giây \((t = 0\) giây khi điểm \(M\) trùng \(A\)). Hỏi thời điểm nào (trong 1 vòng quay đầu tiên) thì điểm \(M\) ở vị trí cao nhất so với mặt nước?
Số giờ có ánh sáng của thành phố \(T\) ở vĩ độ 400 bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số \(d(t) = 3 \cdot \sin \left[ {\frac{\pi }{{182}}(t - 80)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\). Bạn An muốn đi tham quan thành phố \(T\) nhưng lại không thích ánh sáng mặt trời, vậy bạn An nên chọn đi vào ngày nào trong năm để thành phố \(T\) có ít giờ có ánh sáng mặt trời nhất?