Đề kiểm tra Hai đường thẳng song song (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trong một mặt phẳng thì hai đường thẳng đó
song song.
chéo nhau.
cắt nhau.
trùng nhau.
Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó
đồng quy.
tạo thành tam giác.
trùng nhau.
cùng song song với một mặt phẳng.
Cho tứ diện ABCD, gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\). Gọi \(G\) là trọng tâm tam giác \(BCD\). Đường thẳng \(AG\) cắt đường thẳng nào trong các đường thẳng dưới đây? 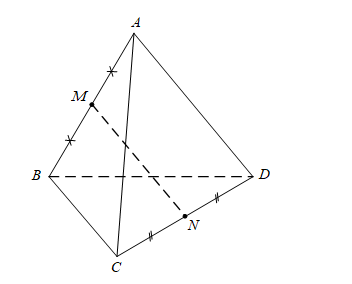
Đường thẳng \(MN\).
Đường thẳng \(CM\).
Đường thẳng \(DN\).
Đường thẳng \(CD\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm \(O\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(SA\) và \(SC\). Đường thẳng \(IJ\) song song với đường thẳng nào?
\(BC\).
\(AC\).
\(SO\).
\(BD\).
Trong mặt phẳng \(\left( P \right)\), cho hình bình hành ABCD. Vẽ các tia \(Bx,Cy,Dz\) song song với nhau, nằm cùng phía với mặt phẳng \(\left( {ABCD} \right)\), đồng thời không nằm trong mặt phẳng \(\left( {ABCD} \right)\). Một mặt phẳng đi qua \(A\), cắt \(Bx,Cy,Dz\) tương ứng tại \(B',C',D'\) sao cho \(BB' = 2\), \(DD' = 4\). Tính \(CC'\).
\(6\).
\(8\).
\(2\).
\(3\).
Cho tứ diện ABCD. Gọi \(G\) và \(E\) lần lượt là trọng tâm của tam giác \(ABD\) và \(ABC\). Mệnh đề nào dưới đây đúng ?
\(GE{\rm{//}}CD\).
\(GE\) cắt \(AD\).
\(GE\) cắt \(CD\).
\(GE\) và \(CD\) chéo nhau.
Cho tứ diện ABCD. Trên các cạnh \(AB,\,\,AD\) lần lượt lấy các điểm \(M\,,\,\,N\) sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}\). Gọi \(P\,,\,\,Q\) lần lượt là trung điểm các cạnh \(CD\,,\,\,CB\). Mệnh đề nào sau đây đúng
Tứ giác\(MNPQ\) là một hình thang.
Tứ giác \(MNPQ\) là hình bình hành.
Bốn điểm \(M\,,\,N\,,\,P\,,\,Q\) không đồng phẳng.
Tứ giác \(MNPQ\) không có các cặp cạnh đối nào song song.
Cho hình chóp S.ABCD. Gọi \(A'\,,\,\,B',\,\,C',\,\,D'\) lần lượt là trung điểm của các cạnh \(SA\,,\,\,SB,\,\,SC,\,\,SD\). Trong các đường thẳng sau đây, đường thẳng nào không song song với \(A'B'\,\,?\)
\(AB\).
\(CD\).
\(C'D'\).
\(SC\).
Cho tứ diện ABCD. Các điểm \(M\,,\,\,N\) lần lượt là trung điểm \(BD\,,\,\,AD\). Các điểm\(H,\,\,G\) lần lượt là trọng tâm các tam giác \(BCD\,\,;\,\,ACD\). Đường thẳng \(HG\) chéo với đưởng thẳng nào sau đây?
\(MN\).
\(CD\).
\(CN\).
\(AB\).
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Điểm \(M\) thuộc cạnh \(SC\) sao cho \(SM = 3MC\), \(N\) là giao điểm của \(SD\) và \(\left( {MAB} \right)\). Khi đó, hai đường thẳng \(CD\) và \(MN\) là hai đường thẳng:
Cắt nhau.
Chéo nhau.
Song song.
Có hai điểm chung.
Cho hình chóp S.ABCD có đáy là hình chữ nhật. Mặt phẳng \(\left( P \right)\) cắt các cạnh \(SA\), \(SB\), \(SC\), \(SD\) lần lượt tại \[M\], \(N\), \(P\), \(Q\). Gọi \(I\) là giao điểm của \(MQ\) và \(NP\). Câu nào sau đây đúng?
\(SI{\rm{//}}AB\).
\(SI{\rm{//}}AC\).
\(SI{\rm{//}}AD\).
\(SI{\rm{//}}BD\).
Cho hình chóp S.ABCD có đáy là hình thang đáy lớn là \(CD\). Gọi \(M\) là trung điểm của cạnh \(SA\), \(N\) là giao điểm của cạnh \(SB\) và mặt phẳng \(\left( {MCD} \right)\). Mệnh đề nào sau đây là mệnh đề đúng?
\[MN\]và \(SD\) cắt nhau.
\[MN\,\parallel \,CD\].
\[MN\] và \(SC\) cắt nhau.
\[MN\] và \(CD\) chéo nhau.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian cho ba đường thẳng \(a,b\) và \(c\) phân biệt. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
b) Nếu hai đường thẳng cùng chéo nhau với đường thẳng thứ ba thì chúng chéo nhau.
c) Nếu đường thẳng \(a\) song song với đường thẳng \(b\), đường thẳng \(b\) và đường thẳng \(c\) chéo nhau thì đường thẳng \(a\) và đường thẳng \(c\) chéo nhau hoặc cắt nhau.
d) Nếu đường thẳng \(a\) cắt \(b\), hai đường thẳng \(b\) và \(c\) chéo nhau thì \(a\) và \(c\) chéo nhau hoặc song song với nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình thang (\(AD\) là đáy lớn, \(BC\) là đáy nhỏ). Gọi \(E,F\) lần lượt là trung điểm của \(SA\) và \(SD\). \(K\) là giao điểm của các đường thẳng \(AB\) và \(CD\). Khi đó:
a) Giao điểm \(M\) của đường thẳng \(SB\) và mặt phẳng \((CDE)\) là điểm thuộc đường thẳng \(KE\)
b) Đường thẳng \(SC\) cắt mặt phẳng \((EFM)\) tại \(N\). Tứ giác \(EFNM\) là hình bình hành
c) Các đường thẳng \(AM,DN,SK\) cùng đi qua một điểm
d) Cho biết \(AD = 2BC\). Tỉ số diện tích của hai tam giác \(KMN\) và \(KEF\) bằng \(\frac{{{S_{\Delta KMN}}}}{{{S_{\Delta KEF}}}} = \frac{2}{3}\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Khi đó
a) Giao tuyến của \((SAB)\) và \((SCD)\) là đường thẳng đi qua \(S\) và song song với \(AB\)
b) Giao tuyến \((SAD)\)và \((SBC)\) là đường thẳng đi qua \(S\) và song song với \(AB\)
c) Gọi \(M \in SC\), giao tuyến của \((ABM)\) và \((SCD)\) là đường thẳng đi qua \(M\) và song song với \(AB\)
d) Gọi \(N \in SB\), giao tuyến của \((SAB)\) và \((NCD)\) là đường thẳng đi qua \(N\) và song song với \(AB\)
Cho hình chóp S.ABCD, có đáy ABCD là một hình bình hành tâm \(O\). Gọi \(I,K\) lần lượt là trung điểm của \(SB\) và \(SD\). Khi đó:
a) \(SO\) là giao tuyến của \((SAC)\) và \((SBD)\)
b) Giao điểm \(J\) của \(SA\) với \((CKB)\) thuộc đường thẳng đi qua \(K\) và song song với \(DC\)
c) Giao tuyến của \((OIA)\) và \((SCD)\) là đường thẳng đi qua \(C\) và song song với \(SD\)
d) \(CD//IJ\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB,BC,CD,DA lần lượt tại các điểm M,N,P,Q.
a) Chứng minh rằng các đường thẳng \(MN,PQ,AC\) đôi một song song hoặc đồng quy.
b) Chứng minh rằng các đường thẳng \(MQ,NP,BD\) đôi một song song hoặc đồng quy.
Cho hình chóp S.ABCD có đáy ABCD là hình thang \((AB//CD)\). Gọi \(M,N\) lần lượt là các điểm thuộc các cạnh \(SA,SD\).
a) Xác định giao tuyến \(d\) của hai mặt phẳng \((MCD)\) và \((NAB)\).
b) Chứng minh rằng \(d//AB\).
Cho tứ diện ABCD có \(I\,;\,\,J\) lần lượt là trọng tâm của tam giác \(ABC\), \(ABD\). Chứng minh rằng: \(IJ{\rm{//}}CD\).
Cho tứ diện ABCD. Trên \(SA,BC\) lấy điểm \(M,N\) sao cho: \(\frac{{SM}}{{SA}} = \frac{{BN}}{{BC}} = \frac{3}{4}\). Qua \(N\) kẻ \(NP\) song song với \(CA\) (\(P\) thuộc \(AB\)). Chứng minh rằng \(MP\)//\(SB\)
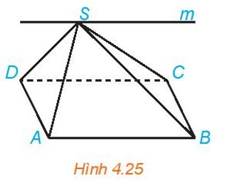
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.25). Hãy xác định giao tuyến của hai mặt phẳng \((SAD)\) và \((SBC)\).
Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.
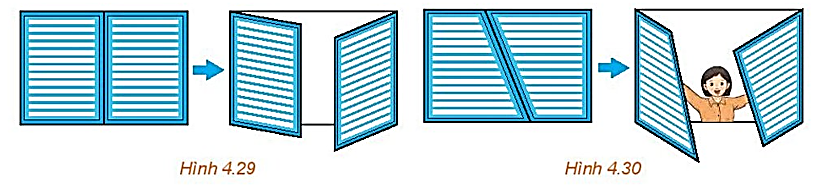
Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau hay không?






